Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T12:14:43.398Z Has data issue: false hasContentIssue false
  • English
  • Français

Functors and ordinal notations. I: A functorial construction of the veblen hierarchy

Published online by Cambridge University Press:  12 March 2014

Jean-Yves Girard  and
Jacqueline Vauzeilles
Jean-Yves Girard
Affiliation:
Université ParisVII, Paris, France
Jacqueline Vauzeilles
Affiliation:
Université ParisVII, Paris, France
Get access Rights & Permissions [Opens in a new window]

Extract

This paper is the first of several works: the matter is the systematic rewriting of usual results of ordinal notations, using Π½-logic. The purpose of these articles is already realized in Π½-logic, in a relatively abstract form; also, they are examples for Π½-logic. The first and second articles in this series are complete versions of unpublished results that one of authors had announced in 1976.

Veblen introduced his hierarchy in 1908. The hierarchy has since been widely used in proof theory; in fact, what is actually needed is the more natural hierarchy: 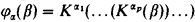, with 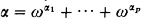(not necessarily a Cantor normal form) and K the Veblen hierarchy.

We shall show:

i) φ is in fact a two-variables functor (denoted by V in the text) commuting with direct limits and with pull-backs.

ii) The property of commutation with pull-backs permits one to give a representation of each ordinal x < φα(0) by means of a finite sequence of ordinals < α. This representation is independent of α it is ⊆ x, and can be used in the building up of notations systems. This representation is the “blowing-up” of the Cantor normal form, and it corresponds exactly to the denotation of ordinals < φα(0) by means of the functions (φβ)β<α.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 49 , Issue 3 , September 1984 , pp. 713 - 729
Copyright
Copyright © Association for Symbolic Logic 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[G]Girard, Jean-Yves, Π½-logic. I: Dilators, Annals of Mathematical Logic, vol. 21 (1981), pp. 75–219.CrossRefGoogle Scholar
[V]Veblen, Oswald, Continuous increasing functions of finite and transfinite ordinals, Transactions of the American Mathematical Society, vol. 9 (1908), pp. 280–292.CrossRefGoogle Scholar