Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-23T22:22:10.322Z Has data issue: false hasContentIssue false
  • English
  • Français

Equality and lyndon's interpolation theorem

Published online by Cambridge University Press:  12 March 2014

Nobuyoshi Motohashi
Nobuyoshi Motohashi*
Affiliation:
University of Tsukuba, Sakura-Mura, Niihari-Gun Ibaraki 3051, Japan
Get access Rights & Permissions [Opens in a new window]

Extract

In this paper, we remark on some properties of equality that tend to be neglected and use them to give a proof of an extension of Lyndon's interpolation theorem. Let LK be a first order classical predicate calculus and LK= a first order classical predicate calculus with equality. We assume that LK and LK= have the propositional constant Τ (truth). For each formula F in LK=, let Rel+ (F), Rel− (F), Rel(F), and Fun(F) be the set of all the predicate symbols which occur in F positively, the set of all the predicate symbols which occur in F negatively, the set of all the predicate symbols which occur in F, and the set of all the function symbols which occur in F.

Theorem A (Lyndon [5]). Suppose that A and B are sentences in LK such that A ⊃ B is provable in LK. Then there is a sentence C in LK such that:

(i) A ⊃ C and C ⊃ B are provable in LK;

(ii) 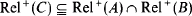and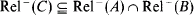

(iii) .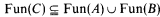

The sentence C which satisfies (i), (ii), (iii) in Theorem A is said to be an interpolant for A ⊃ B in Theorem A. Note that condition (iii) is not included in the original form of Lyndon's interpolation theorem (cf. [5]), but we can easily add this condition. Also, there is some obscurity in the original formulation with regard to the equality symbol. For example, Lyndon writes: “The theorem takes the same form whether or not we admit a predicate denoting identity, with suitable axioms, to the predicate calculus” [5, p. 129].

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 49 , Issue 1 , March 1984 , pp. 123 - 128
Copyright
Copyright © Association for Symbolic Logic 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Fujiwara, T., A generalization of the Lyndon-Keisler theorem on homomorphism and its applications to interpolation theorem, Journal of the Mathematical Society of Japan, vol. 30 (1978), pp. 278–302.CrossRefGoogle Scholar
[2]Hailperin, T., Remarks on identity and description in first-order axiom systems, this Journal vol. 19 (1954), pp. 14–20.Google Scholar
[3]Keisler, H. J., Model theory for infinitary logic, North-Holland, Amsterdam, 1971.Google Scholar
[4]Lopez-Escobar, E. G. K., An interpolation theorem for denumerably long formulas, Fundamenta Mathematical, vol. 57 (1965), pp. 253–272.CrossRefGoogle Scholar
[5]Lyndon, R. C., An interpolation theorem in the predicate calculus, Pacific Journal of Mathematics, vol. 9 (1959), pp. 129–142.CrossRefGoogle Scholar
[6]Motohashi, N., Elimination theorems of unigueness conditions, Zeitschrift fur Mathematische Logik und Grundlagen der Mathematik, vol. 28 (1983), pp. 29–44.Google Scholar
[7]Oberschelp, A., On the Craig-Lyndon interpolation theorem, this Journal vol. 33 (1968), pp. 271–274.Google Scholar
[8]Schütte, K., Der Interpolationssatz in der intuitionistischen Pradikatenlogik, Mathematische Annalen, vol. 148 (1962), pp. 192–200.CrossRefGoogle Scholar
[9]Shoenfield, J. R., Mathematical Logic, Addison-Wesley, London, 1967.Google Scholar
[10]Takeuti, G., Proof theory, North-Holland, Amsterdam, 1975.Google Scholar