No CrossRef data available.
Article contents
A downward Löwenheim-Skolem theorem for infinitary theories which have the unsuperstability property
Published online by Cambridge University Press: 12 March 2014
Abstract
We present a downward Löwenheim-Skolem theorem which transfers downward formulas from L∞,ω
to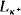 
, ω. The simplest instance is:
Theorem 1. Let λ > κ be infinite cardinals, and let L be a similarity type of cardinality κ at most. For every L-structure M of cardinality λ and every X ⊆ M there exists a model N ≺ M containing the set X of power ∣X∣ · κ such that for every pair of finite sequences a, b ∈ N
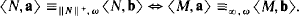
The following theorem is an application:
Theorem 2. Let λ<κ, T ∈ 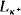, ω, and suppose χ is a Ramsey cardinal greater than λ. If T has the (χ, 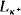, ω)-unsuperstability property, then T has the (χ, 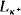, ω)-unsuperstability property.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1988
Footnotes
1
I would like to thank John Baldwin for asking me a question which is the reason why I wrote this paper, and for his valuable remarks on the first draft. This research was partially supported by NSF grant DMS-8603167.
References
REFERENCES
[Ch] Chang, C. C., Some remarks on the model theory of infinitary languages, The syntax and semantics of infinitary languages (Barwise, J., editor), Lecture Notes in Mathematics, vol. 72, Springer-Verlag, Berlin, 1968, pp. 36–63.CrossRefGoogle Scholar
[Di] Dickmann, M. A., larger infinitary languages, Model-theoretic logics (Barwise, J. and Feferman, S., editors), Springer-Verlag, Berlin, 1985, pp. 317–363.Google Scholar
[GS] Gale, D. and Stewart, F. M., Infinite games with perfect information, Contributions to the theory of games. II (Kuhn, H. W. and Tucker, A. W., editors), Princeton University Press, Princeton, New Jersey, 1953, pp. 245–266.Google Scholar
[GrSh] Grossberg, R. and Shelah, S., A non structure theorem for an infinitary theory which has the unsuperstability property, Illinois Journal of Mathematics, vol. 30 (1986), pp. 364–390.CrossRefGoogle Scholar
[He] Henkin, L., Some remarks on infinitely long formulas, Infinitistic methods: proceedings of the symposium on foundations of mathematics, PWN, Warsaw, and Pergamon Press, Oxford, 1961, pp. 167–183.Google Scholar
[Kar] Karp, C., Finite quantifier equivalence, The theory of models (Addison, J. W.
et al., editors), North-Holland, Amsterdam, 1965, pp. 405–412.Google Scholar
[Kel] Keisler, H. J., Formulas with linearly ordered quantifiers, The syntax and semantics of infinitary languages (Barwise, J., editor), Lecture Notes in Mathematics, vol. 72, Springer-Verlag, Berlin, 1968, pp. 96–130.Google Scholar
[Ke2] Keisler, H. J., Model theory for infinitary logic, North-Holland, Amsterdam, 1971.Google Scholar
[Ko] Kolaitis, PH. G., Game quantification, Model-theoretic logics (Barwise, J. and Feferman, S., editors), Springer-Verlag, 1985, pp. 365–421.Google Scholar
[Ma] Malitz, J., Problems in the model theory of infinite languages, Ph.D. thesis, University of California, Berkeley, California, 1966.Google Scholar
[Sh1] Shelah, S., On the number of non-almost isomorphic models of Tin a power, Pacific Journal Mathematics, vol. 36 (1971), pp. 811–818.CrossRefGoogle Scholar
[Sh2] Shelah, S., A combinatorial problem; stability and order for models and theories in infinitary languages, Pacific Journal of Mathematics, vol. 41 (1972), pp. 247–267.CrossRefGoogle Scholar
[Sh3] Shelah, S., Classification theory and the number of non-isomorphic models, North-Holland, Amsterdam, 1978.Google Scholar