Article contents
Deux remarques à propos de la propriété de recouvrement fini
Published online by Cambridge University Press: 12 March 2014
Extract
Cette note est consacrée à quelques compléments à mon article [6], que le lecteur est supposé avoir sous les yeux, et qui traite de la propriété de recouvrement fini, de Keisler. Je rappelle seulement ici que:
a) La définition originale est la suivante: une théorie complète T n'a pas la p.r.f. si à toute formule f(x, ȳ) de son langage est associé un entier n, de sorte que tout ensemble (fini!) {f(x, ā1), …, f(x, ās)}, où les āi; sont des paramètres extraits d'un modèle M de T, soit consistant dès que ses parties à n éléments le sont. Une théorie sans p.r.f. satisfait done un renforcement du théorème de compacité; elle est en ce sens plus simple qu'une théorie avec p.r.f.
b) T n'a pas la p.r.f. si et seulement si elle est stable (i.e. tout type sur un modèle M de T est définissable; à toute formule f(x, ȳ) est associée une formule g(ȳ, ā) à paramètres dans M, telle que les 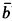 de M pour lesquels f(x,
de M pour lesquels f(x, 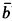 ) est dans le type en question soient précisément ceux qui vérifient g(ȳ, ā)), et si en outre on peut exprimer par une formule sur le paramètre ā que g(ȳ, ā) définit un f-type consistant: à f1(x, ȳ), …, fs(x, ȳ), g1(ȳ,
) est dans le type en question soient précisément ceux qui vérifient g(ȳ, ā)), et si en outre on peut exprimer par une formule sur le paramètre ā que g(ȳ, ā) définit un f-type consistant: à f1(x, ȳ), …, fs(x, ȳ), g1(ȳ, 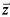 ), …, gs(ȳ,
), …, gs(ȳ, 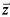 ) est associé une formule h(
) est associé une formule h(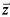 ), telle que pour tout ā de tout modèle M de T, ā satisfasse h si et seulement si l'ensemble de tous les fi(x,
), telle que pour tout ā de tout modèle M de T, ā satisfasse h si et seulement si l'ensemble de tous les fi(x, 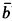 ), où
), où 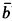 est dans M et satisfait gi(ȳ, ā), est consistant.
est dans M et satisfait gi(ȳ, ā), est consistant.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1984
References
RÉFÉRENCES
- 3
- Cited by


