Published online by Cambridge University Press: 12 March 2014
The present note offers a short argument for the descent theorems of Zawadowski [10] (originally [9]) and Makkai [6], which were conjectured by Pitts after the descent theorem of Joyal and Tierney [3] for open geometric morphisms of (Grothendieck) toposes. The original proofs, which involve variants of Makkai's [5] duality for first order logic, are rather involved and there has been considerable interest in locating simpler proofs. Viewed categorically, the descent theorems establish a bicategorical exactness property (conservative morphisms are effective descent) for pretop (the 2-category of small pretoposes, pretopos functors, and natural transformations), for exact (exact categories, exact functors, and natural transformations), and for bpretop* (Boolean pretoposes, pretopos functors, and natural isomorphisms). Viewed logically, they fragment into a familiar Beth/Tarski-type definability theorem and a covering theorem for certain functors on PCΔ-categories (groupoids, in the Boolean case); the latter (as the former) is a 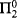 arithmetical statement about the syntax of first order logic ([6, §3])).
arithmetical statement about the syntax of first order logic ([6, §3])).
The argument here involves special models and, independently, a continuity lemma of Makkai. The use of special models is axiomatic in that only a few properties (listed below) are needed. The continuity lemma, 9.1 of [6], is established via forcing and can be read independently of the rest of that paper. Because of its interest to both the model theorist and the category theorist, the argument is first given as straight model theory and afterwards it is briefly indicated how the descent theorems follow.