Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T06:50:57.786Z Has data issue: false hasContentIssue false
  • English
  • Français

Countable models of nonmultidimensional ℵ0-stable theories

Published online by Cambridge University Press:  12 March 2014

Elisabeth Bouscaren  and
Daniel Lascar
Elisabeth Bouscaren
Affiliation:
Université Paris VII, 75251 Paris, France
Daniel Lascar
Affiliation:
Université Paris VII, 75251 Paris, France
Get access Rights & Permissions [Opens in a new window]

Extract

In this paper T will always be a countable ℵ0-stable theory, and in this introduction a model of T will mean a countable model.

One of the main notions we introduce is that of almost homogeneous model: we say that a model M of T is almost homogeneous if for all ā and 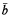finite sequences of elements in M, if the strong type of ā is the same as the strong type of 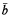(i.e. for all equivalence relations E, definable over the empty set and with a finite number of equivalence classes, ā and 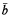are in the same equivalence class), then there is an automorphism of M taking ā to 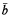. Although this is a weaker notion than homogeneity, these models have strong properties, and it can be seen easily that the Scott formula of any almost homogeneous model is in L1. In fact, Pillay [Pi.] has shown that almost homogeneous models are characterized by the set of types they realize.

The motivation of this research is to distinguish two classes of ℵ0-Stable theories:

(1) theories such that all models are almost homogeneous;

(2) theories with 2ℵ0 nonalmost homogeneous models.

The example of theories with Skolem functions [L. 1] (almost homogeneous is then equivalent to homogeneous) seems to indicate a link between these properties and the notion of multidimensionality, and that nonmultidimensional theories are in the first case.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 48 , Issue 1 , March 1983 , pp. 197 - 205
Copyright
Copyright © Association for Symbolic Logic 1983

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[B.]Bouscaren, E., Countable models of multidimensional ℵ0-stable theories, this Journal (to appear).Google Scholar
[L.1]Lascar, D., Les modèles dénombrables d'une théorie ayant des fonctions de Skolem, Transactions of the American Mathematical Society, vol. 268 (1981), pp. 345–366.Google Scholar
[L.2]Lascar, D., Ordre de Rudin-Keisler et poids dans les théories stables, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik (to appear).Google Scholar
[L.P.]Lascar, D. and Poizat, B., An introduction to forking, this Journal, vol. 44 (1979), pp. 330–350.Google Scholar
[Pi.]Pillay, A., Weakly homogeneous models (to appear).Google Scholar
[Sh.]Shelah, S., Classification theory and the number of non-isomorphic models, North-Holland, Amsterdam, 1978.Google Scholar