Published online by Cambridge University Press: 12 March 2014
A relational structure 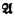 of cardinality ℵ0 is called homogeneous by Fraissé [1] if each isomorphism between finite substructures of
of cardinality ℵ0 is called homogeneous by Fraissé [1] if each isomorphism between finite substructures of 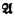 can be extended to an automorphism of
can be extended to an automorphism of 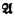 . In §1 of this paper it is shown that there are
. In §1 of this paper it is shown that there are 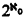 isomorphism types of such structures for the first order language L0 with a single (binary) relation symbol, answering a question raised by Fraissé. In fact, as is shown in §2, a family of
isomorphism types of such structures for the first order language L0 with a single (binary) relation symbol, answering a question raised by Fraissé. In fact, as is shown in §2, a family of 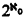 nonisomorphic homogeneous structures for L0 can be constructed, each member
nonisomorphic homogeneous structures for L0 can be constructed, each member 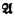 of which satisfies the following conditions (where U is the homogeneous, ℵ0-universal graph, the structure of which is considered in [4]):
of which satisfies the following conditions (where U is the homogeneous, ℵ0-universal graph, the structure of which is considered in [4]):
(i) The relation R of 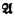 is asymmetric (R ∩ R−1 = ∅);
is asymmetric (R ∩ R−1 = ∅);
(ii) If A is the domain of 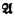 and S is the symmetric relation R ∪ R−1, then (A, S) is isomorphic to U. That is, each
and S is the symmetric relation R ∪ R−1, then (A, S) is isomorphic to U. That is, each 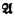 may be regarded as the result of assigning a unique direction to each edge of the graph U.
may be regarded as the result of assigning a unique direction to each edge of the graph U.
Let T0 be the first order theory of all homogeneous structures for L0 which have cardinality ℵ0. In §3 (which can be read independently of §2) it is shown that T0 has 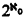 complete extensions (in L0), each of which is ℵ0-categorical. Moreover, among the complete extensions of T0 are theories of arbitrary (preassigned) degree of unsolvability. In particular, there exists an undecidable, ℵ0-categorieal theory in L0, which answers a question raised by Grzegorczyk [2], [3].
complete extensions (in L0), each of which is ℵ0-categorical. Moreover, among the complete extensions of T0 are theories of arbitrary (preassigned) degree of unsolvability. In particular, there exists an undecidable, ℵ0-categorieal theory in L0, which answers a question raised by Grzegorczyk [2], [3].
It follows from Theorem 6 of [3] that there are ℵ0-categorical theories of partial orderings which have arbitrarily high degrees of unsolvability. This is in sharp contrast to the situation for linear orderings, which were the motivation for Fraissé's early work. Indeed, as is shown in [10], every ℵ0-categorical theory of a linear ordering is finitely axiomatizable. (W. Glassmire [12] has independently shown the existence of 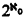 theories in L0 which are all ℵ0-categorical, and C. Ash [13] has independently shown that such theories exist with arbitrary degree of unsolvability.)
theories in L0 which are all ℵ0-categorical, and C. Ash [13] has independently shown that such theories exist with arbitrary degree of unsolvability.)