Hostname: page-component-6bf8c574d5-gr6zb Total loading time: 0 Render date: 2025-02-25T16:54:36.549Z Has data issue: false hasContentIssue false
  • English
  • Français

COMPUTABLE LINEAR ORDERS AND PRODUCTS

Part of: Model theory Computability and recursion theory

Published online by Cambridge University Press:  20 July 2020

ANDREY N. FROLOV ,
STEFFEN LEMPP ,
KENG MENG NG  and
GUOHUA WU
ANDREY N. FROLOV
Affiliation:
HIGHER INSTITUTE OF INFORMATION TECHNOLOGY AND INTELLIGENT SYSTEMS KAZAN FEDERAL UNIVERSITYKAZAN420008 , RUSSIAE-mail: [email protected]
STEFFEN LEMPP
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF WISCONSINMADISON, WI53706-1388, USAE-mail: [email protected]: http://www.math.wisc.edu/∼lempp/
KENG MENG NG
Affiliation:
SCHOOL OF PHYSICAL AND MATHEMATICAL SCIENCES NANYANG TECHNOLOGICAL UNIVERSITYSINGAPORE637371, REPUBLIC OF SINGAPOREE-mail: [email protected]: http://www3.ntu.edu.sg/home/kmng/E-mail: [email protected]: http://www3.ntu.edu.sg/home/guohua/
GUOHUA WU
Affiliation:
SCHOOL OF PHYSICAL AND MATHEMATICAL SCIENCES NANYANG TECHNOLOGICAL UNIVERSITYSINGAPORE637371, REPUBLIC OF SINGAPOREE-mail: [email protected]: http://www3.ntu.edu.sg/home/kmng/E-mail: [email protected]: http://www3.ntu.edu.sg/home/guohua/
Get access Rights & Permissions [Opens in a new window]

Abstract

We characterize the linear order types 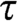$\tau $ with the property that given any countable linear order 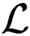$\mathcal {L}$ , 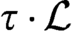$\tau \cdot \mathcal {L}$ is a computable linear order iff 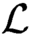$\mathcal {L}$ is a computable linear order, as exactly the finite nonempty order types.

Keywords

computable linear orderproduct

MSC classification

Primary: 03D45: Theory of numerations, effectively presented structures
Secondary: 03C57: Effective and recursion-theoretic model theory
Type
Articles
Information
The Journal of Symbolic Logic , Volume 85 , Issue 2 , June 2020 , pp. 605 - 623
Copyright
© The Association for Symbolic Logic 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Alaev, P., Thurber, J., and Frolov, A., Computability on linear orderings enriched with predicates . Algebra and Logic, vol. 48 (2009), no. 5, pp. 313–320.CrossRefGoogle Scholar
Ash, C. and Knight, J., Computable Structures and the Hyperarithmetical Hierarchy, Studies in Logic and the Foundations of Mathematics, vol. 144, North-Holland Publishing, Amsterdam, Netherlands, 2000.Google Scholar
Downey, R., Computability theory and linear orders , Handbook of Recursive Mathematics vol. 2 (Ershov, Y. L., Goncharov, S. S., Nerode, A., and Remmel, J. B., editors), Studies in Logic and the Foundations of Mathematics, Elsevier, Amsterdam, Netherlands, 1998, pp. 823–976.Google Scholar
Downey, R. and Knight, J., Orderings with $\alpha$ -th jump degree 0(α) . Proceedings of the American Mathematical Society, vol. 114 (1992), pp. 545–552.Google Scholar
Fellner, S., Recursive and finite axiomatizability of linear orderings , Ph.D. thesis, Rutgers, New Brundswick, NJ, 1976.Google Scholar
Frolov, A., $\Delta^0_2$ copies of linear orderings . Algebra and Logic, vol. 45 (2006), no. 3, pp. 201–209.CrossRefGoogle Scholar
Frolov, A., Linear orderings coding theorems . Uchenye Zapiski Kazanskogo Universiteta. Seriya Fiziko-Matematicheskie Nauki, vol. 154 (2012), no. 2, pp. 142–151.Google Scholar