Published online by Cambridge University Press: 12 March 2014
Priority arguments have been used to produce r.e. sets whose complements have various properties (e.g., maximal sets, hyperhypersimple sets, etc.). In this paper we use the priority method in the context of certain recursively presented models (e.g., dense unbordered linear orderings, countable atomless Boolean algebras, infinite dimensional vector spaces over a finite field) to produce hypersimple subsets of these models whose complements are closed under algebraic operations and/or whose complements are elementarily isomorphic to certain algebraic substructures. For example, it follows from the results of §3 that there are hypersimple subsets of a countable atomless Boolean algebra (of an infinite dimensional vector space over a finite field) in every nonzero r.e. degree whose complement is a subalgebra (subspace). Also, it follows from the same result that, given any 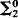 subset P of the rationals Q, there is a hypersimple subset of Q whose complement is order isomorphic to P.
subset P of the rationals Q, there is a hypersimple subset of Q whose complement is order isomorphic to P.
A model M of a theory T in a countable language L is said to be recursively presented if the universe ∣M∣ of M is an initial segment of the natural numbers and the satisfaction relation “a satisfies Φ in M” is recursive (where a is a finite sequence of elements of ∣M∣ and Φ is a formula in L).