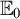1. Introduction
For a set X and
![]() $k \in {\mathbb {N}}$
, we use
$k \in {\mathbb {N}}$
, we use
![]() $[X]^k$
to denote the set of all k-element subsets of X. When
$[X]^k$
to denote the set of all k-element subsets of X. When
![]() $A \subseteq X$
, we let
$A \subseteq X$
, we let ![]() be the complement of A. All graphs in this paper are simple, i.e., a graph G consists of a vertex set
be the complement of A. All graphs in this paper are simple, i.e., a graph G consists of a vertex set
![]() $V(G)$
and an edge set
$V(G)$
and an edge set
![]() $E(G) \subseteq [V(G)]^2$
. When there is no chance of confusion, we use the standard graph-theoretic convention and write
$E(G) \subseteq [V(G)]^2$
. When there is no chance of confusion, we use the standard graph-theoretic convention and write
![]() $xy$
instead of
$xy$
instead of
![]() $\{x,y\}$
to indicate an edge joining vertices x and y. The line graph
$\{x,y\}$
to indicate an edge joining vertices x and y. The line graph
![]() $L(G)$
of a graph G is defined by
$L(G)$
of a graph G is defined by

We say that a graph L is a line graph if it is isomorphic to the line graph of some graph G. Beineke famously characterized all line graphs by a list of nine forbidden induced subgraphs:
Theorem 1.1 (Beineke [Reference Beineke1])
A graph is a line graph if and only if it does not have an induced subgraph isomorphic to any of the nine graphs in Figure 1.

Figure 1 The nine graphs of Beineke.
We are interested in extending Beineke’s result to the setting of Borel graphs, that is, graphs G such that
![]() $V(G)$
is a standard Borel space and
$V(G)$
is a standard Borel space and
![]() $E(G)$
is a Borel subset of
$E(G)$
is a Borel subset of
![]() $[V(G)]^2$
. (We refer the reader unfamiliar with such terminology to Kechris’s book on descriptive set theory [Reference Kechris8]; we also review some necessary descriptive set-theoretic background in Section 2.) The systematic study of Borel graphs and their combinatorics was initiated in the landmark 1999 paper by Kechris, Solecki, and Todorcevic [Reference Kechris, Solecki and Todorcevic12], who applied descriptive set theory to the study of graph colorings. This launched the development of the highly fruitful field of descriptive combinatorics, which has connections to many areas of mathematics, including group theory, measure theory, ergodic theory, theoretical computer science, and more. For an overview of the field, see the 2020 survey by Kechris and Marks [Reference Kechris and Marks10] and the 2021 survey by Pikhurko [Reference Pikhurko and Dabrowski16].
$[V(G)]^2$
. (We refer the reader unfamiliar with such terminology to Kechris’s book on descriptive set theory [Reference Kechris8]; we also review some necessary descriptive set-theoretic background in Section 2.) The systematic study of Borel graphs and their combinatorics was initiated in the landmark 1999 paper by Kechris, Solecki, and Todorcevic [Reference Kechris, Solecki and Todorcevic12], who applied descriptive set theory to the study of graph colorings. This launched the development of the highly fruitful field of descriptive combinatorics, which has connections to many areas of mathematics, including group theory, measure theory, ergodic theory, theoretical computer science, and more. For an overview of the field, see the 2020 survey by Kechris and Marks [Reference Kechris and Marks10] and the 2021 survey by Pikhurko [Reference Pikhurko and Dabrowski16].
Borel graphs G and H are Borel isomorphic, in symbols
![]() $G \cong _B H$
, if there exists a Borel isomorphism from G to H (i.e., a graph isomorphism
$G \cong _B H$
, if there exists a Borel isomorphism from G to H (i.e., a graph isomorphism
![]() $f \colon V(G) \to V(H)$
that is a Borel function). Note that the line graph
$f \colon V(G) \to V(H)$
that is a Borel function). Note that the line graph
![]() $L(G)$
of a Borel graph G is itself a Borel graph. We say that a Borel graph L is a Borel line graph if there exists a Borel graph G such that
$L(G)$
of a Borel graph G is itself a Borel graph. We say that a Borel graph L is a Borel line graph if there exists a Borel graph G such that
![]() $L \cong _B{L(G)}$
. Clearly, if a graph is a Borel line graph, then it is both a Borel graph and a line graph. Conversely, we ask the following:
$L \cong _B{L(G)}$
. Clearly, if a graph is a Borel line graph, then it is both a Borel graph and a line graph. Conversely, we ask the following:
Given a Borel graph that is a line graph, when is it a Borel line graph?
To demonstrate that this question is nontrivial, let us give an example of a Borel graph that is a line graph but not a Borel line graph. Recall that the Cantor space is the set ![]() of countably infinite binary strings endowed with the product topology, where the topology on
of countably infinite binary strings endowed with the product topology, where the topology on
![]() $\{0,1\}$
is discrete. The equivalence relation
$\{0,1\}$
is discrete. The equivalence relation
![]() $\mathbb {E}_0$
is defined on
$\mathbb {E}_0$
is defined on
![]() $\mathcal {C}$
by relating two elements if they are equal after some index; that is, given
$\mathcal {C}$
by relating two elements if they are equal after some index; that is, given
![]() $\alpha $
,
$\alpha $
,
![]() $\beta \in \mathcal {C}$
, we have
$\beta \in \mathcal {C}$
, we have
This is a Borel equivalence relationFootnote
1
with countable classes (for a survey on such equivalence relations, see the recent manuscript by Kechris [Reference Kechris9]). From
![]() $\mathbb {E}_0$
, we define a graph
$\mathbb {E}_0$
, we define a graph
![]() $\mathbb {K}_0$
as follows:
$\mathbb {K}_0$
as follows:
In other words,
![]() $\mathbb {K}_0$
is obtained by making every
$\mathbb {K}_0$
is obtained by making every
![]() $\mathbb {E}_0$
-equivalence class into a clique. Then
$\mathbb {E}_0$
-equivalence class into a clique. Then
![]() $\mathbb {K}_0$
is a Borel graph, and, being a collection of vertex-disjoint cliques, it is a line graph (a clique is isomorphic to the line graph of a star). However,
$\mathbb {K}_0$
is a Borel graph, and, being a collection of vertex-disjoint cliques, it is a line graph (a clique is isomorphic to the line graph of a star). However,
![]() $\mathbb {K}_0$
is not a Borel line graph. This essentially boils down to the fact that the relation
$\mathbb {K}_0$
is not a Borel line graph. This essentially boils down to the fact that the relation
![]() $\mathbb {E}_0$
is not smooth (see Definition 2.8), as if
$\mathbb {E}_0$
is not smooth (see Definition 2.8), as if
![]() $\mathbb {K}_0$
were a Borel line graph, the map picking out the center of the star corresponding to each component of
$\mathbb {K}_0$
were a Borel line graph, the map picking out the center of the star corresponding to each component of
![]() $\mathbb {K}_0$
would witness that
$\mathbb {K}_0$
would witness that
![]() $\mathbb {E}_0$
is smooth. Another simple proof uses Borel chromatic numbers:
$\mathbb {E}_0$
is smooth. Another simple proof uses Borel chromatic numbers:
Definition 1.2 (Borel chromatic number)
Given a graph G, a proper coloring of G is a function
![]() $f : V(G) \to C$
, where C is some set, such that for all
$f : V(G) \to C$
, where C is some set, such that for all
![]() ${xy \in E(G)}$
,
${xy \in E(G)}$
,
![]() $f(x) \neq f(y)$
. The chromatic number of G, denoted by
$f(x) \neq f(y)$
. The chromatic number of G, denoted by
![]() $\chi (G)$
, is the smallest cardinality of a set C such that G has a proper coloring
$\chi (G)$
, is the smallest cardinality of a set C such that G has a proper coloring
![]() $f \colon V(G) \to C$
. For a Borel graph G, its Borel chromatic number,
$f \colon V(G) \to C$
. For a Borel graph G, its Borel chromatic number,
![]() $\chi _B(G)$
, is the smallest cardinality of a standard Borel space X such that there exists a Borel proper coloring
$\chi _B(G)$
, is the smallest cardinality of a standard Borel space X such that there exists a Borel proper coloring
![]() $f \colon V(G) \to X$
.
$f \colon V(G) \to X$
.
A standard Baire category argument proves that
![]() $\chi _B(\mathbb {K}_0)> \aleph _0$
[Reference Kechris and Marks10, p. 27]. On the other hand, if
$\chi _B(\mathbb {K}_0)> \aleph _0$
[Reference Kechris and Marks10, p. 27]. On the other hand, if
![]() $\mathbb {K}_0$
were a Borel line graph, then by the Feldman–Moore theorem (see Theorem 1.4), we would have
$\mathbb {K}_0$
were a Borel line graph, then by the Feldman–Moore theorem (see Theorem 1.4), we would have
![]() $\chi _B(\mathbb {K}_0) \leqslant \aleph _0$
. It follows that
$\chi _B(\mathbb {K}_0) \leqslant \aleph _0$
. It follows that
![]() $\mathbb {K}_0$
is not a Borel line graph.
$\mathbb {K}_0$
is not a Borel line graph.
Given a graph G and a subset
![]() $U \subseteq V(G)$
, we let
$U \subseteq V(G)$
, we let
![]() $G[U]$
denote the subgraph of G induced by the vertices of U, i.e.,
$G[U]$
denote the subgraph of G induced by the vertices of U, i.e., ![]() . Given graphs G and H, we say that G contains a copy of H if G has an induced subgraph isomorphic to H, i.e., if there exists a set
. Given graphs G and H, we say that G contains a copy of H if G has an induced subgraph isomorphic to H, i.e., if there exists a set
![]() $U \subseteq V(G)$
such that
$U \subseteq V(G)$
such that
![]() $G[U] \cong H$
. Similarly, if G and H are Borel graphs, we say that G contains a Borel copy of H if there exists a Borel set
$G[U] \cong H$
. Similarly, if G and H are Borel graphs, we say that G contains a Borel copy of H if there exists a Borel set
![]() $U \subseteq V(G)$
such that
$U \subseteq V(G)$
such that
![]() $G[U] \cong _B H$
. It is clear that the property of being a Borel line graph is preserved under taking Borel induced subgraphs. Therefore, for a Borel graph to be a Borel line graph, it must contain no copies of the nine forbidden subgraphs of Beineke nor a Borel copy of
$G[U] \cong _B H$
. It is clear that the property of being a Borel line graph is preserved under taking Borel induced subgraphs. Therefore, for a Borel graph to be a Borel line graph, it must contain no copies of the nine forbidden subgraphs of Beineke nor a Borel copy of
![]() $\mathbb {K}_0$
Footnote
2
. Our main result is that the converse is true, i.e.,
$\mathbb {K}_0$
Footnote
2
. Our main result is that the converse is true, i.e.,
![]() $\mathbb {K}_0$
is the only additional obstruction in the Borel setting.
$\mathbb {K}_0$
is the only additional obstruction in the Borel setting.
Theorem 1.3. Let L be a Borel graph. Then L is a Borel line graph if and only if it contains neither a copy of any of the nine graphs of Beineke nor a Borel copy of
![]() $\mathbb {K}_0$
.
$\mathbb {K}_0$
.
In view of Theorem 1.1, the above statement is equivalent to the assertion that a Borel graph L is a Borel line graph if and only if it is a line graph that does not contain a Borel copy of
![]() $\mathbb {K}_0$
.
$\mathbb {K}_0$
.
As an immediate consequence of Theorem 1.3, we obtain a characterization of locally countable Borel line graphs in terms of their Borel chromatic numbers. This follows from the graph-theoretic version of the Feldman–Moore theorem [Reference Feldman and Moore3] due to Kechris, Solecki, and Todorcevic [Reference Kechris, Solecki and Todorcevic12], which states that locally countable Borel line graphs have countable Borel chromatic numbers.
Theorem 1.4 (Feldman–Moore: Graph version [Reference Kechris, Solecki and Todorcevic12, Theorem 4.10])
If L is a locally countable Borel line graph, then
![]() $\chi _B(L) \leqslant \aleph _0$
.
$\chi _B(L) \leqslant \aleph _0$
.
As mentioned above,
![]() $\chi _B({\mathbb {K}_0})> \aleph _0$
, and thus Theorems 1.1 and 1.3 imply the following partial converse to the Feldman–Moore theorem:
$\chi _B({\mathbb {K}_0})> \aleph _0$
, and thus Theorems 1.1 and 1.3 imply the following partial converse to the Feldman–Moore theorem:
Corollary 1.5. Let L be a locally countable Borel graph. If L is a line graph and
![]() $\chi _B(L) \leqslant \aleph _0$
, then L is a Borel line graph.
$\chi _B(L) \leqslant \aleph _0$
, then L is a Borel line graph.
Theorem 1.3 allows the Feldman–Moore theorem to be stated in terms of forbidden subgraphs:
Corollary 1.6. If L is a locally countable Borel graph that contains neither a copy of any of the nine graphs of Beineke nor a Borel copy of
![]() $\mathbb {K}_0$
, then
$\mathbb {K}_0$
, then
![]() $\chi _{B}(L) \leqslant \aleph _0$
.
$\chi _{B}(L) \leqslant \aleph _0$
.
An intriguing question is whether the hypotheses of Corollary 1.6 can be weakened. For instance, it would be interesting to know if forbidding only some of the nine graphs of Beineke together with
![]() $\mathbb {K}_0$
is enough to reach the same conclusion. This line of inquiry can be naturally viewed as an extension to the Borel setting of the theory of
$\mathbb {K}_0$
is enough to reach the same conclusion. This line of inquiry can be naturally viewed as an extension to the Borel setting of the theory of
![]() $\chi $
-boundedness [Reference Seymour and Scott17], which aims to bound the chromatic number of a graph with certain forbidden substructures by a function of its clique number. More broadly, our work indicates the prospect of fruitful interactions between descriptive set theory and structural (as opposed to extremal or probabilistic) graph theory and leads to general problems such as what other natural classes of Borel graphs can be characterized by means of excluding certain Borel induced subgraphs.
$\chi $
-boundedness [Reference Seymour and Scott17], which aims to bound the chromatic number of a graph with certain forbidden substructures by a function of its clique number. More broadly, our work indicates the prospect of fruitful interactions between descriptive set theory and structural (as opposed to extremal or probabilistic) graph theory and leads to general problems such as what other natural classes of Borel graphs can be characterized by means of excluding certain Borel induced subgraphs.
The remainder of the paper is organized as follows. In Section 2, we review some necessary background and tools from descriptive set theory. A reader familiar with descriptive set theory may proceed directly to Section 3, where we provide a road map for the proof of Theorem 1.3. The rest of the paper contains proofs of the intermediate theorems and lemmas needed in the proof of Theorem 1.3.
2. Tools from descriptive set theory
In this section, we provide some fundamental tools from descriptive set theory and the study of Borel equivalence relations. Our main references for descriptive set theory are [Reference Kechris8; Reference Tserunyan18], and the reader is invited to consult them for any background not mentioned here.
A standard Borel space is a set X equipped with a
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\mathfrak {B}(X)$
(called Borel subsets) that coincides with the Borel
$\mathfrak {B}(X)$
(called Borel subsets) that coincides with the Borel
![]() $\sigma $
-algebra generated by some Polish (i.e., separable completely metrizable) topology on X. All uncountable standard Borel spaces are isomorphic [Reference Kechris8, Theorem 15.6], so there is usually no loss of generality in assuming that X is some specific space such as
$\sigma $
-algebra generated by some Polish (i.e., separable completely metrizable) topology on X. All uncountable standard Borel spaces are isomorphic [Reference Kechris8, Theorem 15.6], so there is usually no loss of generality in assuming that X is some specific space such as
![]() $\mathbb {R}$
or the Cantor space
$\mathbb {R}$
or the Cantor space
![]() $\mathcal {C}$
. If X is a standard Borel space and
$\mathcal {C}$
. If X is a standard Borel space and
![]() $A \subseteq X$
is a Borel set, then A equipped with the
$A \subseteq X$
is a Borel set, then A equipped with the
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\{B \cap A \,:\, B \in \mathfrak {B}(X)\}$
is also a standard Borel space [Reference Kechris8, Corollary 13.4]. A function
$\{B \cap A \,:\, B \in \mathfrak {B}(X)\}$
is also a standard Borel space [Reference Kechris8, Corollary 13.4]. A function
![]() $f \colon X \to Y$
between two standard Borel spaces is Borel if for every Borel set
$f \colon X \to Y$
between two standard Borel spaces is Borel if for every Borel set
![]() $A \subseteq Y$
, its preimage
$A \subseteq Y$
, its preimage
![]() $f^{-1}(A)$
is a Borel subset of X. Equivalently, a function
$f^{-1}(A)$
is a Borel subset of X. Equivalently, a function
![]() $f \colon X \to Y$
is Borel if and only if
$f \colon X \to Y$
is Borel if and only if ![]() is a Borel subset of
is a Borel subset of
![]() $X \times Y$
[Reference Kechris8, Theorem 14.12].
$X \times Y$
[Reference Kechris8, Theorem 14.12].
It is often convenient to describe a subset
![]() $B \subseteq X$
via a statement
$B \subseteq X$
via a statement
![]() $P(x)$
with one free variable x such that
$P(x)$
with one free variable x such that
![]() $B = \{x \in X \,:\, P(x)\}$
. To verify such a set B is Borel, we will usually not explicitly write its definition out set-theoretically, but instead rely on the form of the statement
$B = \{x \in X \,:\, P(x)\}$
. To verify such a set B is Borel, we will usually not explicitly write its definition out set-theoretically, but instead rely on the form of the statement
![]() $P(x)$
itself, keeping in mind that conjunctions and universal quantifiers (resp. disjunctions and existential quantifiers) in
$P(x)$
itself, keeping in mind that conjunctions and universal quantifiers (resp. disjunctions and existential quantifiers) in
![]() $P(x)$
correspond to intersections (resp. unions) in the construction of B, while negations correspond to complements.
$P(x)$
correspond to intersections (resp. unions) in the construction of B, while negations correspond to complements.
Let X be a standard Borel space. The diagonal of X is the set
Note that
![]() $\Delta (X)$
is a Borel subset of
$\Delta (X)$
is a Borel subset of
![]() $X^2$
(it is the graph of the identity function on X). Now consider the map
$X^2$
(it is the graph of the identity function on X). Now consider the map
![]() $\mathsf {pair} \colon X^2 \setminus \Delta (X) \to [X]^2$
given by
$\mathsf {pair} \colon X^2 \setminus \Delta (X) \to [X]^2$
given by ![]() . We endow
. We endow
![]() $[X]^2$
with the
$[X]^2$
with the
![]() $\sigma $
-algebra
$\sigma $
-algebra
This makes
![]() $[X]^2$
a standard Borel space [Reference Kechris and Miller11, Example 6.1 and Proposition 6.3]. By construction, the function
$[X]^2$
a standard Borel space [Reference Kechris and Miller11, Example 6.1 and Proposition 6.3]. By construction, the function
![]() $\mathsf {pair} \colon X^2 \setminus \Delta (X) \to [X]^2$
is Borel.
$\mathsf {pair} \colon X^2 \setminus \Delta (X) \to [X]^2$
is Borel.
Definition 2.1 (Analytic and coanalytic sets)
Let X be a standard Borel space. A set
![]() $A \subseteq X$
is analytic if there exist a standard Borel space Y and a Borel function
$A \subseteq X$
is analytic if there exist a standard Borel space Y and a Borel function
![]() $f : Y \to X$
such that
$f : Y \to X$
such that
![]() $f(Y) = A$
. Equivalently, A is analytic if there exist a standard Borel space Y and a Borel set
$f(Y) = A$
. Equivalently, A is analytic if there exist a standard Borel space Y and a Borel set
![]() $B \subseteq X \times Y$
such that
$B \subseteq X \times Y$
such that
![]() $x \in A \iff \exists \, y \in Y\, ((x,y) \in B)$
. A set
$x \in A \iff \exists \, y \in Y\, ((x,y) \in B)$
. A set
![]() $A \subseteq X$
is coanalytic if its complement is analytic.
$A \subseteq X$
is coanalytic if its complement is analytic.
In practice, to show a set A is analytic we will typically write
where
![]() $P(x,y)$
is a statement with two free variables such that
$P(x,y)$
is a statement with two free variables such that
![]() $P(x,y)$
holds if and only if
$P(x,y)$
holds if and only if
![]() $(x,y) \in B$
for some Borel set
$(x,y) \in B$
for some Borel set
![]() $B \subseteq X \times Y$
. Verifying that
$B \subseteq X \times Y$
. Verifying that
![]() $P(x,y)$
really does correspond to a Borel set will often be routine and left to the reader. Similarly, a set
$P(x,y)$
really does correspond to a Borel set will often be routine and left to the reader. Similarly, a set
![]() $A \subseteq X$
is coanalytic when
$A \subseteq X$
is coanalytic when
where
![]() $P(x,y)$
describes a Borel subset of
$P(x,y)$
describes a Borel subset of
![]() $X \times Y$
. We give an example of a proof of this type below; in the sequel, equally straightforward arguments will be omitted.
$X \times Y$
. We give an example of a proof of this type below; in the sequel, equally straightforward arguments will be omitted.
Example 2.2. For a Borel graph G, the set
![]() $I \subseteq V(G)$
of all isolated vertices is coanalytic. Indeed,
$I \subseteq V(G)$
of all isolated vertices is coanalytic. Indeed,
To see that the set
![]() $\{(x,y) \in V(G)^2 \,:\, xy \notin E(G)\}$
is Borel, we observe that it is equal to
$\{(x,y) \in V(G)^2 \,:\, xy \notin E(G)\}$
is Borel, we observe that it is equal to
It follows that the set I is coanalytic.
The family of all analytic subsets of a standard Borel space is closed under countable unions and intersections, and the same is true for the family of all coanalytic subsets [Reference Kechris8, Proposition 14.4].
Example 2.3. We argue that for a Borel graph G, the equivalence relation
![]() $\equiv _G$
whose classes are the connected components of G is analytic. Indeed, we have
$\equiv _G$
whose classes are the connected components of G is analytic. Indeed, we have
 $$ \begin{align*} x \equiv_G y \iff \exists\, d \in {\mathbb{N}}, \, \exists\, &(u_0, \ldots, u_d) \in V(G)^{d+1}\\ &\big(x = u_0, \, u_0u_1 \in E(G), \, \ldots, \, u_{d-1}u_d \in E(G),\, u_d = y\big). \end{align*} $$
$$ \begin{align*} x \equiv_G y \iff \exists\, d \in {\mathbb{N}}, \, \exists\, &(u_0, \ldots, u_d) \in V(G)^{d+1}\\ &\big(x = u_0, \, u_0u_1 \in E(G), \, \ldots, \, u_{d-1}u_d \in E(G),\, u_d = y\big). \end{align*} $$
This means that we can write
![]() ${\equiv _G} = \bigcup _{d \in {\mathbb {N}}} S_d$
, where
${\equiv _G} = \bigcup _{d \in {\mathbb {N}}} S_d$
, where
 $$ \begin{align*} (x,y) \in S_d \iff \exists\, &(u_0, \ldots, u_d) \in V(G)^{d+1}\\ &\big(x = u_0, \, u_0u_1 \in E(G), \, \ldots, \, u_{d-1}u_d \in E(G),\, u_d = y\big). \end{align*} $$
$$ \begin{align*} (x,y) \in S_d \iff \exists\, &(u_0, \ldots, u_d) \in V(G)^{d+1}\\ &\big(x = u_0, \, u_0u_1 \in E(G), \, \ldots, \, u_{d-1}u_d \in E(G),\, u_d = y\big). \end{align*} $$
Since
![]() $E(G)$
is Borel, we see that each set
$E(G)$
is Borel, we see that each set
![]() $S_d$
is analytic, and hence their union is analytic as well.
$S_d$
is analytic, and hence their union is analytic as well.
It should be noted that there exist analytic sets that are not Borel. This follows from a diagonalization argument originally given by Suslin, see [Reference Kechris8, Theorem 14.2]. We now present a classical result of Luzin and Novikov that provides a sufficient condition for an analytic set to be Borel. A proof can be found in [Reference Kechris8, Theorem 18.10] or [Reference Miller15, Theorem 32].
Theorem 2.4 (Luzin–Novikov)
Let X and Y be standard Borel spaces and let
![]() ${B \subseteq X \times Y}$
be a Borel set. If for every
${B \subseteq X \times Y}$
be a Borel set. If for every
![]() $x \in X$
, the set
$x \in X$
, the set
![]() $\{y \in Y : (x,y) \in B\}$
is countable, then
$\{y \in Y : (x,y) \in B\}$
is countable, then
is a Borel subset of X.
Example 2.5. Thanks to the Luzin–Novikov theorem, many combinatorial constructions on locally countable Borel graphs can be shown to result in Borel sets. For instance, as in Example 2.2, let
![]() $I \subseteq V(G)$
be the set of all isolated vertices of G. Then
$I \subseteq V(G)$
be the set of all isolated vertices of G. Then
If G is a locally countable Borel graph, then for each
![]() $x \in V(G)$
, the set
$x \in V(G)$
, the set
![]() $\{y \in V(G) \,:\, xy \in E(G)\}$
is countable, and hence, by the Luzin–Novikov theorem, the set
$\{y \in V(G) \,:\, xy \in E(G)\}$
is countable, and hence, by the Luzin–Novikov theorem, the set
![]() $I^c$
is Borel. It follows that the set of all isolated vertices in a locally countable Borel graph is Borel. A similar argument shows that for a locally countable Borel graph G, the relation
$I^c$
is Borel. It follows that the set of all isolated vertices in a locally countable Borel graph is Borel. A similar argument shows that for a locally countable Borel graph G, the relation
![]() $\equiv _G$
defined in Example 2.3 is Borel.
$\equiv _G$
defined in Example 2.3 is Borel.
Another classical theorem of Suslin allows separating two analytic sets by a Borel set. A proof can be found in [Reference Kechris8, Theorem 14.7].
Theorem 2.6 (Analytic separation)
Let
![]() $A_1$
and
$A_1$
and
![]() $A_2$
be disjoint analytic subsets of a standard Borel space X. Then there exists a Borel set
$A_2$
be disjoint analytic subsets of a standard Borel space X. Then there exists a Borel set
![]() $B \subseteq X$
such that
$B \subseteq X$
such that
![]() $A_1 \subseteq B \subseteq A_2^c$
.
$A_1 \subseteq B \subseteq A_2^c$
.
An immediate corollary of Theorem 2.6 is that a set that is both analytic and coanalytic must be Borel, since it can be separated from its complement by a Borel set.
Given a set X and an equivalence relation E on X, we say a set
![]() $A \subseteq X$
is E-invariant if no element of A is related by E to an element of
$A \subseteq X$
is E-invariant if no element of A is related by E to an element of
![]() $A^c$
. The following result is [Reference Kechris8, Exercise 14.14]; we provide a proof for completeness.
$A^c$
. The following result is [Reference Kechris8, Exercise 14.14]; we provide a proof for completeness.
Lemma 2.7 (Invariant analytic separation)
Let X be a standard Borel space and let E be an analytic equivalence relation on X. Suppose Y,
![]() $Z \subseteq X$
are analytic sets such that no element of Y is E-related to an element of Z. Then there is an E-invariant Borel set
$Z \subseteq X$
are analytic sets such that no element of Y is E-related to an element of Z. Then there is an E-invariant Borel set
![]() $B \subseteq X$
such that
$B \subseteq X$
such that
![]() $Y \subseteq B \subseteq Z^c$
.
$Y \subseteq B \subseteq Z^c$
.
Proof. Given
![]() $A \subseteq X$
, let
$A \subseteq X$
, let
![]() $[A]_E$
be the E-saturation of A, i.e.,
$[A]_E$
be the E-saturation of A, i.e.,
Observe that the set
![]() $[A]_E$
is E-invariant; furthermore, since E is analytic, if A is analytic, then
$[A]_E$
is E-invariant; furthermore, since E is analytic, if A is analytic, then
![]() $[A]_E$
is analytic as well. Upon replacing Y by
$[A]_E$
is analytic as well. Upon replacing Y by
![]() $[Y]_E$
and Z by
$[Y]_E$
and Z by
![]() $[Z]_E$
, we may assume that Y and Z are E-invariant and disjoint.
$[Z]_E$
, we may assume that Y and Z are E-invariant and disjoint.
We will now inductively define an increasing sequence of Borel sets
![]() $(B_i)_{i \in {\mathbb {N}}}$
such that
$(B_i)_{i \in {\mathbb {N}}}$
such that
![]() $Y \subseteq B_i \subseteq Z^c$
and
$Y \subseteq B_i \subseteq Z^c$
and
![]() $[B_i]_E \subseteq B_{i+1}$
. We do so as follows: by analytic separation, there exists a Borel set
$[B_i]_E \subseteq B_{i+1}$
. We do so as follows: by analytic separation, there exists a Borel set
![]() $B_0$
such that
$B_0$
such that
![]() $Y \subseteq B_0 \subseteq Z^c$
. Now let
$Y \subseteq B_0 \subseteq Z^c$
. Now let
![]() $B_i$
be Borel with
$B_i$
be Borel with
![]() ${Y \subseteq B_i \subseteq Z^c}$
. Since B is Borel, it follows
${Y \subseteq B_i \subseteq Z^c}$
. Since B is Borel, it follows
![]() $[B_i]_E$
is analytic; furthermore, as
$[B_i]_E$
is analytic; furthermore, as
![]() $B_i \subseteq Z^c$
and Z is E-invariant, it follows
$B_i \subseteq Z^c$
and Z is E-invariant, it follows
![]() $[B_i]_E \subseteq Z^c$
. Thus by analytic separation there exists Borel
$[B_i]_E \subseteq Z^c$
. Thus by analytic separation there exists Borel
![]() $B_{i+1}$
with
$B_{i+1}$
with
![]() $[B_i]_E \subseteq B_{i+1} \subseteq Z^c$
. This completes the inductive construction.
$[B_i]_E \subseteq B_{i+1} \subseteq Z^c$
. This completes the inductive construction.
Let ![]() . Clearly B is Borel and
. Clearly B is Borel and
![]() $Y \subseteq B \subseteq Z^c$
. Finally, since
$Y \subseteq B \subseteq Z^c$
. Finally, since
![]() ${B = \bigcup _{n \in {\mathbb {N}}} [B_n]_E}$
, the set B is E-invariant, as desired.
${B = \bigcup _{n \in {\mathbb {N}}} [B_n]_E}$
, the set B is E-invariant, as desired.
An important role in our arguments will be played by the following special class of equivalence relations on standard Borel spaces:
Definition 2.8 (Smoothness)
Let E be an equivalence relation on a standard Borel space X. Then E is smooth if there exist a standard Borel space Y and Borel function
![]() $f : X \to Y$
such that for all x,
$f : X \to Y$
such that for all x,
![]() $y \in X$
we have
$y \in X$
we have
![]() $x\, E \, y \iff f(x) = f(y)$
. We say f witnesses the smoothness of E.
$x\, E \, y \iff f(x) = f(y)$
. We say f witnesses the smoothness of E.
Note that a smooth equivalence relation on a standard Borel space is automatically Borel. Since all uncountable standard Borel spaces are isomorphic [Reference Kechris8, Theorem 15.6], we may, without loss of generality, use
![]() $\mathbb {R}$
as the codomain of f in Definition 2.8 for concreteness.
$\mathbb {R}$
as the codomain of f in Definition 2.8 for concreteness.
Recall the equivalence relation
![]() $\mathbb {E}_0$
discussed in Section 1. Harrington, Kechris, and Louveau showed that not only is
$\mathbb {E}_0$
discussed in Section 1. Harrington, Kechris, and Louveau showed that not only is
![]() $\mathbb {E}_0$
nonsmooth, but it is a “smallest” nonsmooth equivalence relation [Reference Harrington, Kechris and Louveau5]. This result is known as the
$\mathbb {E}_0$
nonsmooth, but it is a “smallest” nonsmooth equivalence relation [Reference Harrington, Kechris and Louveau5]. This result is known as the
![]() $\mathbb {E}_0$
-dichotomy. While the original proof due to Harrington, Kechris, and Louveau uses methods of effective descriptive set theory, a classical, graph-theoretic proof was given by Miller [Reference Miller15, Theorem 26].
$\mathbb {E}_0$
-dichotomy. While the original proof due to Harrington, Kechris, and Louveau uses methods of effective descriptive set theory, a classical, graph-theoretic proof was given by Miller [Reference Miller15, Theorem 26].
Theorem 2.9 (
 $\mathbb {E}_0$
-dichotomy)
$\mathbb {E}_0$
-dichotomy)
Let X be a standard Borel space and let E be a Borel equivalence relation on X. Then exactly one of the following holds
![]() $:$
$:$
-
(1) E is smooth, or
-
(2) there exists a Borel embedding from
 $\mathbb {E}_0$
to E; that is, there is an injective Borel function
$\mathbb {E}_0$
to E; that is, there is an injective Borel function
 $f : \mathcal {C} \to X$
such that
$f : \mathcal {C} \to X$
such that
 $\alpha \, \mathbb {E}_0 \, \beta \iff f(\alpha )\, E\, f(\beta )$
.
$\alpha \, \mathbb {E}_0 \, \beta \iff f(\alpha )\, E\, f(\beta )$
.
3. Outline of the proof of Theorem 1.3
3.1. Line graph decompositions and line graph relations
An important role in our arguments in played by a characterization of line graphs via a partition of their edges into cliques, which we call a line graph decomposition.
Definition 3.1 (Line graph decompositions)
A line graph decomposition of a graph L is a collection
![]() $\mathscr {C}$
of nonempty subsets of
$\mathscr {C}$
of nonempty subsets of
![]() $V(L)$
such that:
$V(L)$
such that:
-
• for all
 $C \in \mathscr {C}$
,
$C \in \mathscr {C}$
,
 $L[C]$
is a clique;
$L[C]$
is a clique; -
• the sets
 $E(L[C])$
,
$E(L[C])$
,
 $C \in \mathscr {C}$
are pairwise disjoint and their union is
$C \in \mathscr {C}$
are pairwise disjoint and their union is
 $E(L)$
;
$E(L)$
; -
• each non-isolated vertex of L is contained in exactly two sets in
 $\mathscr {C}$
; each isolated vertex is contained in exactly one set in
$\mathscr {C}$
; each isolated vertex is contained in exactly one set in
 $\mathscr {C}$
.
$\mathscr {C}$
.
Note that any two sets in a line graph decomposition have at most one common vertex. Krausz observed that a graph L is a line graph if and only if L has a line graph decomposition [Reference Krausz13]. Indeed, if
![]() $L = L(G)$
for some graph G, then
$L = L(G)$
for some graph G, then
![]() $\{\{e \in E(G) \,:\, e \ni v\} \,:\, v \in V(G)\}$
is a line graph decomposition of L. Conversely, given a line graph decomposition
$\{\{e \in E(G) \,:\, e \ni v\} \,:\, v \in V(G)\}$
is a line graph decomposition of L. Conversely, given a line graph decomposition
![]() $\mathscr {C}$
of a graph L without isolated vertices, one can form a graph G such that
$\mathscr {C}$
of a graph L without isolated vertices, one can form a graph G such that
![]() $L(G) \cong L$
as follows:
$L(G) \cong L$
as follows:
Here an isomorphism
![]() $\varphi : E(G) \to V(L)$
is given by letting
$\varphi : E(G) \to V(L)$
is given by letting
![]() $\varphi (\{C, C'\})$
for each edge
$\varphi (\{C, C'\})$
for each edge
![]() $\{C,C'\} \in E(G)$
be the unique vertex in
$\{C,C'\} \in E(G)$
be the unique vertex in
![]() $C \cap C'$
. If L has isolated vertices, we simply add to G an isolated edge corresponding to each isolated vertex of L.
$C \cap C'$
. If L has isolated vertices, we simply add to G an isolated edge corresponding to each isolated vertex of L.
Since a line graph decomposition of L induces a partition of the edge set of L, we can use it to define an equivalence relation on
![]() $E(L)$
, called the line graph relation:
$E(L)$
, called the line graph relation:
Definition 3.2 (Line graph relations)
Let
![]() $\mathscr {C}$
be a line graph decomposition of a graph L. The equivalence relation
$\mathscr {C}$
be a line graph decomposition of a graph L. The equivalence relation
on
![]() $E(L)$
is called the line graph relation on L under
$E(L)$
is called the line graph relation on L under
![]() $\mathscr {C}$
. An equivalence relation
$\mathscr {C}$
. An equivalence relation
![]() $\sim $
on
$\sim $
on
![]() $E(L)$
is called a line graph relation if there is a line graph decomposition
$E(L)$
is called a line graph relation if there is a line graph decomposition
![]() $\mathscr {C}$
of L such that
$\mathscr {C}$
of L such that
![]() ${\sim } = {\sim _{\mathscr {C}}}$
.
${\sim } = {\sim _{\mathscr {C}}}$
.
Note that if
![]() $\sim $
is a line graph relation on L, then each
$\sim $
is a line graph relation on L, then each
![]() $\sim $
-class is the edge set of a clique in L. Furthermore, the following combinatorial characterization of line graph relations is an immediate consequence of the above definitions:
$\sim $
-class is the edge set of a clique in L. Furthermore, the following combinatorial characterization of line graph relations is an immediate consequence of the above definitions:
Lemma 3.3 [Reference Beineke1, p. 130]
Let L be a graph. An equivalence relation
![]() $\sim $
on
$\sim $
on
![]() $E(L)$
is a line graph relation if and only if each
$E(L)$
is a line graph relation if and only if each
![]() $\sim $
-equivalence class is the edge set of a clique in L and every vertex of L is incident to at most two
$\sim $
-equivalence class is the edge set of a clique in L and every vertex of L is incident to at most two
![]() $\sim $
-classes.
$\sim $
-classes.
Let G be a graph and let R be a binary relation on
![]() $E(G)$
. If
$E(G)$
. If
![]() $H \subseteq G$
is a subgraph of G, we let
$H \subseteq G$
is a subgraph of G, we let ![]() be the restriction of R to H. If
be the restriction of R to H. If
![]() $U \subseteq V(G)$
, then we let
$U \subseteq V(G)$
, then we let ![]() be the restriction of R to U.
be the restriction of R to U.
Lemma 3.4. Let L be a graph with a line graph relation
![]() $\sim $
. If H is an induced subgraph of L, then
$\sim $
. If H is an induced subgraph of L, then
![]() ${\sim }|_{H}$
is a line graph relation on H.
${\sim }|_{H}$
is a line graph relation on H.
Proof. Follows immediately from Lemma 3.3.
3.2. Main steps of the proof of Theorem 1.3
We can now describe the key steps in the proof of our main result. To begin with, we note that, thanks to Beineke’s Theorem 1.1, Theorem 1.3 is equivalent to the following statement:
Theorem 3.5. Let L be a Borel graph that is a line graph. Then L is a Borel line graph if and only if L does not contain a Borel copy of
![]() $\kern1pt\mathbb {K}_0$
.
$\kern1pt\mathbb {K}_0$
.
A significant complication in proving Theorem 3.5 arises from the fact that L is not assumed to be locally countable. As briefly discussed in Example 2.5, in the study of locally countable Borel graphs, the Luzin–Novikov theorem is routinely used to show that various combinatorially defined sets are Borel, but such arguments are unavailable for general Borel graphs. As a result, even very simple sets associated with L, such as the set of all isolated vertices, may fail to be Borel. This makes analyzing the structure of L through the lens of Borel combinatorics a particularly intricate task.
Let L be a Borel graph that is a line graph. Below we outline the major intermediate results that go into the proof of Theorem 3.5. Each of them presents interesting challenges in its own right, which we will comment on in the subsequent subsections.
Since L is a line graph, it has a line graph decomposition, and hence there is a line graph relation on L. The first step in our proof is to find a Borel line graph relation on L:
Theorem 3.6 (Borel line graph relations)
If L is a Borel graph that is a line graph, then L has a Borel line graph relation.
Proof. Section 4.
Theorem 3.6 yields a Borel line graph relation regardless of whether L is a Borel line graph. The question arises: Given a Borel graph L with a Borel line graph relation
![]() $\sim $
, how can we tell whether L is a Borel line graph? The answer is given by the following theorem:
$\sim $
, how can we tell whether L is a Borel line graph? The answer is given by the following theorem:
Theorem 3.7 (Smooth line graph relations)
Let L be a Borel graph that is a line graph. Then the following are equivalent
![]() $:$
$:$
-
(1) L is a Borel line graph,
-
(2) L has a smooth line graph relation,
-
(3) all Borel line graph relations on L are smooth.
Of the above equivalences, we only use (1)
![]() $\Longleftrightarrow $
(2) in our proof of Theorem 1.3. Still, the equivalence (2)
$\Longleftrightarrow $
(2) in our proof of Theorem 1.3. Still, the equivalence (2)
![]() $\Longleftrightarrow $
(3) is of independent interest, as it is a natural addition to our characterization of Borel line graphs by the smoothness of their Borel line graph relations. The implication (2)
$\Longleftrightarrow $
(3) is of independent interest, as it is a natural addition to our characterization of Borel line graphs by the smoothness of their Borel line graph relations. The implication (2)
![]() $\Rightarrow $
(3) is proved in Appendix 7.1, and the details of (2)
$\Rightarrow $
(3) is proved in Appendix 7.1, and the details of (2)
![]() $\Rightarrow $
(1) are presented in Section 5 (see also Section 3.4 for an informal discussion of this implication). The other implications in Theorem 3.7 are straightforward:
$\Rightarrow $
(1) are presented in Section 5 (see also Section 3.4 for an informal discussion of this implication). The other implications in Theorem 3.7 are straightforward:
Proof. (1)
![]() $\Rightarrow $
(2): Without loss of generality, we may assume that
$\Rightarrow $
(2): Without loss of generality, we may assume that
![]() $L = L(G)$
for some Borel graph G. The following definition gives a line graph relation on
$L = L(G)$
for some Borel graph G. The following definition gives a line graph relation on
![]() $E(L)$
:
$E(L)$
:
The smoothness of
![]() $\sim $
is witnessed by the function
$\sim $
is witnessed by the function
![]() $f: E(L) \to V(G)$
defined by letting
$f: E(L) \to V(G)$
defined by letting
![]() $f(\{e_1, e_2\})$
be the unique vertex in
$f(\{e_1, e_2\})$
be the unique vertex in
![]() $e_1 \cap e_2$
. Therefore, L has a smooth line graph relation.
$e_1 \cap e_2$
. Therefore, L has a smooth line graph relation.
(2)
![]() $\Rightarrow $
(1): Section 5.
$\Rightarrow $
(1): Section 5.
(2)
![]() $\Rightarrow $
(3): Appendix 7.1.
$\Rightarrow $
(3): Appendix 7.1.
(3)
![]() $\Rightarrow $
(2): Follows from Theorem 3.6.
$\Rightarrow $
(2): Follows from Theorem 3.6.
Assuming L is not a Borel line graph, Theorems 3.6 and 3.7 yield a nonsmooth Borel line graph relation
![]() $\sim $
on
$\sim $
on
![]() $E(L)$
, which we utilize in Section 6 to find a desired Borel copy of
$E(L)$
, which we utilize in Section 6 to find a desired Borel copy of
![]() $\mathbb {K}_0$
in L.
$\mathbb {K}_0$
in L.
In the following subsections we describe in a little more detail some of the ideas used in accomplishing these steps.

Figure 2 The four singular graphs.
Table 1 Exceptional graphs in Whitney’s strong isomorphism theorem (left) with the corresponding line graphs (right).

3.3. Finding a Borel line graph relation (Theorem 3.6)
A key ingredient in our proof of Theorem 3.6 is the fact that a connected line graph has a unique line graph decomposition, save for four graphs. This is shown in Corollary 3.9. These four graphs are listed in the second column of Table 1 and illustrated in Figure 2. We call a graph singular if it is isomorphic to any of these 4 graphs, and we call a graph exceptional if its line graph is singular. The exceptional graphs are listed in the first column of Table 1 (here
![]() $K_{1,3}^+$
is
$K_{1,3}^+$
is
![]() $K_{1,3}$
with one additional edge, and
$K_{1,3}$
with one additional edge, and
![]() $K_4^-$
is
$K_4^-$
is
![]() $K_4$
with a single edge removed).
$K_4$
with a single edge removed).
Theorem 3.8 (Whitney’s strong isomorphism theorem)
If G and H are connected non-exceptional graphs, then every isomorphism
![]() $\varphi \colon E(G) \to E(H)$
from
$\varphi \colon E(G) \to E(H)$
from
![]() $L(G)$
to
$L(G)$
to
![]() $L(H)$
is induced by an isomorphism
$L(H)$
is induced by an isomorphism
![]() $\sigma \colon V(G) \to V(H)$
from G to H, that is, if
$\sigma \colon V(G) \to V(H)$
from G to H, that is, if
![]() $xy \in E(G)$
, then
$xy \in E(G)$
, then
![]() $\varphi (xy) = \sigma (x)\sigma (y)$
.
$\varphi (xy) = \sigma (x)\sigma (y)$
.
Whitney [Reference Whitney20] proved Theorem 3.8 for finite graphs in 1932. A short alternative proof was given by Jung [Reference Jung7], who also extended the result to infinite graphs. Jung’s paper is in German; for an English version of the proof, see [Reference Hemminger6] or [Reference Harary4, Theorem 8.3]. We shall apply Theorem 3.8 in the form of the following corollary:
Corollary 3.9 (Uniqueness of line graph decompositions)
If L is a connected nonsingular line graph, then L has a unique line graph decomposition (and thus a unique line graph relation).
Proof. Let L be a connected nonsingular line graph. If L has one vertex, its line graph decomposition is clearly unique. Otherwise, suppose
![]() $\mathscr {C}$
and
$\mathscr {C}$
and
![]() $\mathscr {C}'$
are line graph decompositions of L. Let G and
$\mathscr {C}'$
are line graph decompositions of L. Let G and
![]() $G'$
be the graphs obtained from
$G'$
be the graphs obtained from
![]() $\mathscr {C}$
and
$\mathscr {C}$
and
![]() $\mathscr {C}'$
respectively as in (3.1). Then
$\mathscr {C}'$
respectively as in (3.1). Then
![]() $L(G) \cong L$
and
$L(G) \cong L$
and
![]() $L(G') \cong L$
, say by isomorphisms
$L(G') \cong L$
, say by isomorphisms
![]() $\varphi $
and
$\varphi $
and
![]() $\varphi '$
respectively. By construction, for all
$\varphi '$
respectively. By construction, for all
![]() $C \in \mathscr {C}$
and
$C \in \mathscr {C}$
and
![]() $C' \in \mathscr {C}'$
,
$C' \in \mathscr {C}'$
,
Since ![]() is an isomorphism from
is an isomorphism from
![]() $L(G)$
to
$L(G)$
to
![]() $L(G')$
, by Theorem 3.8,
$L(G')$
, by Theorem 3.8,
![]() $\psi $
is induced by an isomorphism
$\psi $
is induced by an isomorphism
![]() $\sigma $
from G to
$\sigma $
from G to
![]() $G'$
, i.e., if
$G'$
, i.e., if
![]() $\{C,C'\} \in E(G)$
, then
$\{C,C'\} \in E(G)$
, then
![]() $\psi (\{C,C'\}) = \{\sigma (C), \sigma (C')\} \in E(G')$
. Now, for any
$\psi (\{C,C'\}) = \{\sigma (C), \sigma (C')\} \in E(G')$
. Now, for any
![]() $C \in \mathscr {C}$
, we can write
$C \in \mathscr {C}$
, we can write
 $$ \begin{align*} \sigma(C) \,&=\, \{\varphi'(\{\sigma(C),B'\}) \,:\, B' \in N_{G'}(\sigma(C))\} \\ &=\, \{\varphi'(\{\sigma(C), \sigma(B)\}) \,:\, B \in N_G(C)\} \\ &=\, \{\varphi' (\psi(\{C,B\})) \,:\, B \in N_G(C)\} \,=\, \{\varphi(\{C,B\}) \,:\, B \in N_G(C)\}\,=\, C. \end{align*} $$
$$ \begin{align*} \sigma(C) \,&=\, \{\varphi'(\{\sigma(C),B'\}) \,:\, B' \in N_{G'}(\sigma(C))\} \\ &=\, \{\varphi'(\{\sigma(C), \sigma(B)\}) \,:\, B \in N_G(C)\} \\ &=\, \{\varphi' (\psi(\{C,B\})) \,:\, B \in N_G(C)\} \,=\, \{\varphi(\{C,B\}) \,:\, B \in N_G(C)\}\,=\, C. \end{align*} $$
Thus
![]() $C \in \mathscr {C}'$
, and hence
$C \in \mathscr {C}'$
, and hence
![]() $\mathscr {C} \subseteq \mathscr {C}'$
. A symmetrical argument shows that
$\mathscr {C} \subseteq \mathscr {C}'$
. A symmetrical argument shows that
![]() $\mathscr {C}' \subseteq \mathscr {C}$
and thus
$\mathscr {C}' \subseteq \mathscr {C}$
and thus
![]() $\mathscr {C} = \mathscr {C}'$
.
$\mathscr {C} = \mathscr {C}'$
.
With Corollary 3.9 in hand, it is not difficult to argue that if a Borel graph L is a line graph and all its components are nonsingular, then the unique line graph relation on L must be Borel. On the other hand, if all components of L are singular, then in particular they are finite, and it is again straightforward to find a Borel line graph relation on L by picking one of the finitely many such relations on each component of L. (This is an instance of the generally well-understood fact that Borel combinatorics essentially trivialize on Borel graphs with finite components, see, e.g., [Reference Pikhurko and Dabrowski16, Section 5.3] and [Reference Bernshteyn and Weilacher2, Section 2.2].) The difficult case in the proof of Theorem 3.6 is when L has a mixture of singular and nonsingular components. The challenge is that it may be impossible to separate the singular components from the nonsingular ones in a Borel way: the union of all singular components of L is a coanalytic—but not necessarily Borel—set. To overcome this difficulty, we use Corollary 3.9 and the analytic separation theorem to first construct a Borel relation R on
![]() $E(L)$
that induces a line graph relation on every infinite component of L, but can behave arbitrarily on finite components. Next we consider the following two sets:
$E(L)$
that induces a line graph relation on every infinite component of L, but can behave arbitrarily on finite components. Next we consider the following two sets:

These sets are analytic and—by the construction of R—disjoint. With the help of invariant analytic separation (Lemma 2.7), we are able to find a Borel set B such that
![]() $A_1 \subseteq B \subseteq A_2^c$
and B is a union of connected components of L. Since
$A_1 \subseteq B \subseteq A_2^c$
and B is a union of connected components of L. Since
![]() ${B \cap A_2 = \emptyset }$
, every component of L contained in
${B \cap A_2 = \emptyset }$
, every component of L contained in
![]() $B^c$
is finite, which allows us to modify R on
$B^c$
is finite, which allows us to modify R on
![]() $B^c$
to obtain a desired line graph relation on L. The details are presented in Section 4.
$B^c$
to obtain a desired line graph relation on L. The details are presented in Section 4.
The argument sketched above is representative of the techniques used in this paper, in that it involves a series of applications of analytic separation to construct a Borel structure with desirable combinatorial properties. The proof of Theorem 3.7 relies on similar ideas, but with even more rounds of analytic separation.
3.4. Analyzing smooth line graph relations (Theorem 3.7)
The proof of the implication (2)
![]() $\Rightarrow $
(1) is not as straightforward as may initially appear. To indicate the source of the difficulty, let us sketch an obvious naive approach (which ends up failing). Suppose that
$\Rightarrow $
(1) is not as straightforward as may initially appear. To indicate the source of the difficulty, let us sketch an obvious naive approach (which ends up failing). Suppose that
![]() $\sim $
is a smooth line graph relation on L and let
$\sim $
is a smooth line graph relation on L and let
![]() $f \colon E(L) \to \mathbb {R}$
be a Borel function witnessing the smoothness of
$f \colon E(L) \to \mathbb {R}$
be a Borel function witnessing the smoothness of
![]() $\sim $
. This means that for each point x in the image of f,
$\sim $
. This means that for each point x in the image of f,
![]() $f^{-1}(x)$
is a
$f^{-1}(x)$
is a
![]() $\sim $
-class. Recall the endpoints of the edges of each
$\sim $
-class. Recall the endpoints of the edges of each
![]() $\sim $
-class induce a clique in L; let us denote this clique by
$\sim $
-class induce a clique in L; let us denote this clique by
![]() $C_x \subseteq V(L)$
. For
$C_x \subseteq V(L)$
. For
![]() $x \in \mathbb {R} \setminus \mathrm {im}(f)$
, set
$x \in \mathbb {R} \setminus \mathrm {im}(f)$
, set ![]() . In an attempt to mimic (3.1), let us consider the graph G with
. In an attempt to mimic (3.1), let us consider the graph G with ![]() and
and
and define a map
![]() $\varphi \colon E(G) \to V(L)$
by letting
$\varphi \colon E(G) \to V(L)$
by letting
![]() $\varphi (xy)$
for each edge
$\varphi (xy)$
for each edge
![]() $xy \in E(G)$
be the (necessarily unique) vertex in
$xy \in E(G)$
be the (necessarily unique) vertex in
![]() $C_x \cap C_y$
. Ideally,
$C_x \cap C_y$
. Ideally,
![]() $\varphi $
witnesses
$\varphi $
witnesses
![]() $L(G) \cong _B L$
by
$L(G) \cong _B L$
by
![]() $\varphi $
. Unfortunately, there are two issues with the construction:
$\varphi $
. Unfortunately, there are two issues with the construction:
-
• First, the map
 $\varphi $
defined in this way is an embedding of
$\varphi $
defined in this way is an embedding of
 $L(G)$
into L, but it is only surjective if every vertex of L is incident to exactly two
$L(G)$
into L, but it is only surjective if every vertex of L is incident to exactly two
 $\sim $
-classes. In general, some vertices of L may be incident to one
$\sim $
-classes. In general, some vertices of L may be incident to one
 $\sim $
-class or be isolated. Note that the set of all isolated vertices, as well as the set of all vertices incident to a single
$\sim $
-class or be isolated. Note that the set of all isolated vertices, as well as the set of all vertices incident to a single
 $\sim $
-class, need not be Borel.
$\sim $
-class, need not be Borel. -
• The second problem is that the set
 $E(G)$
defined above is analytic but not necessarily Borel. In other words, G may fail to be a Borel graph.
$E(G)$
defined above is analytic but not necessarily Borel. In other words, G may fail to be a Borel graph.
The crux of the difficulty here is that the following relation may not be Borel:
To circumvent this obstacle, we repeatedly apply analytic separation to construct a sequence
![]() $R_0$
,
$R_0$
,
![]() $R_1$
,
$R_1$
,
![]() $R_2$
,
$R_2$
,
![]() $R_3$
,
$R_3$
,
![]() $R_4$
,
$R_4$
,
![]() $R_5$
of Borel relations that in some sense “approximate” R. With care, we are able to ensure that the final relation,
$R_5$
of Borel relations that in some sense “approximate” R. With care, we are able to ensure that the final relation,
![]() $R_5$
, has the following properties:
$R_5$
, has the following properties:
-
•
 $R \subseteq R_5$
, and if
$R \subseteq R_5$
, and if
 $v \, R_5 \, x$
and
$v \, R_5 \, x$
and
 $x \in \mathrm {im}(f)$
, then
$x \in \mathrm {im}(f)$
, then
 $v \, R\, x$
,
$v \, R\, x$
, -
• every vertex of
 $L\ R_5$
-relates to at most two elements of
$L\ R_5$
-relates to at most two elements of
 $\mathbb {R}$
,
$\mathbb {R}$
, -
• every element of
 $\mathbb {R} \setminus \mathrm {im}(f)\ R_5$
-relates to at most one vertex of L.
$\mathbb {R} \setminus \mathrm {im}(f)\ R_5$
-relates to at most one vertex of L.
We then show that these properties enable us to use
![]() $R_5$
in place of R in the construction of a Borel graph G with
$R_5$
in place of R in the construction of a Borel graph G with
![]() $L(G) \cong _B L$
. The details are given in Section 5.
$L(G) \cong _B L$
. The details are given in Section 5.
3.5. Finishing the proof
Let L be a Borel graph with a nonsmooth Borel line graph relation
![]() $\sim $
. To obtain a Borel copy of
$\sim $
. To obtain a Borel copy of
![]() $\mathbb {K}_0$
in L, we seek a Borel induced subgraph
$\mathbb {K}_0$
in L, we seek a Borel induced subgraph
![]() $H \subseteq L$
such that:
$H \subseteq L$
such that:
-
• every component of H is a clique, and
-
• the equivalence relation
 $\equiv _H$
on
$\equiv _H$
on
 $V(H)$
whose classes are the components of H is nonsmooth.
$V(H)$
whose classes are the components of H is nonsmooth.
Once we find such H, we can take
![]() $\varphi \colon \mathcal {C} \to V(H)$
to be a Borel embedding from
$\varphi \colon \mathcal {C} \to V(H)$
to be a Borel embedding from
![]() $\mathbb {E}_0$
to
$\mathbb {E}_0$
to
![]() $\equiv _H$
guaranteed by the
$\equiv _H$
guaranteed by the
![]() $\mathbb {E}_0$
-dichotomy and observe that
$\mathbb {E}_0$
-dichotomy and observe that
![]() $L[\mathrm {im}(\varphi )]$
is a Borel copy of
$L[\mathrm {im}(\varphi )]$
is a Borel copy of
![]() $\mathbb {K}_0$
in L, as desired.
$\mathbb {K}_0$
in L, as desired.
To motivate our construction of H, note that since
![]() $\sim $
is nonsmooth, the
$\sim $
is nonsmooth, the
![]() $\mathbb {E}_0$
-dichotomy yields a Borel embedding
$\mathbb {E}_0$
-dichotomy yields a Borel embedding
![]() $\rho \colon \mathcal {C} \to E(L)$
from
$\rho \colon \mathcal {C} \to E(L)$
from
![]() $\mathbb {E}_0$
to
$\mathbb {E}_0$
to
![]() $\sim $
. In particular, if
$\sim $
. In particular, if
![]() $\alpha $
,
$\alpha $
,
![]() $\beta \in \mathcal {C}$
are not
$\beta \in \mathcal {C}$
are not
![]() $\mathbb {E}_0$
-related, then
$\mathbb {E}_0$
-related, then
![]() $\rho (\alpha ) \not \sim \rho (\beta )$
. We want to strengthen this property as follows:
$\rho (\alpha ) \not \sim \rho (\beta )$
. We want to strengthen this property as follows:
 $$ \begin{align} &\textit{If}\ \alpha, \beta \in \mathcal{C}\ \textit{are not}\ \mathbb{E}_0\text{-}\textit{related},\ \textit{then the endpoints of the edge}\ \rho(\alpha)\ \textit{are not adjacent}\nonumber\\ &\textit{to the endpoints of}\ \rho(\beta). \end{align} $$
$$ \begin{align} &\textit{If}\ \alpha, \beta \in \mathcal{C}\ \textit{are not}\ \mathbb{E}_0\text{-}\textit{related},\ \textit{then the endpoints of the edge}\ \rho(\alpha)\ \textit{are not adjacent}\nonumber\\ &\textit{to the endpoints of}\ \rho(\beta). \end{align} $$
It is not hard to see that if (3.2) holds, we can let H be the subgraph of L induced by the vertices incident to
![]() $\mathrm {im}(\rho )$
. In order to find
$\mathrm {im}(\rho )$
. In order to find
![]() $\rho $
satisfying (3.2), we rely on the following lemma:
$\rho $
satisfying (3.2), we rely on the following lemma:
Lemma 3.10. Let X be a standard Borel space and let
![]() $E \subseteq X^2$
be a nonsmooth Borel equivalence relation on X. If
$E \subseteq X^2$
be a nonsmooth Borel equivalence relation on X. If
![]() $R \subseteq X^2$
is a Borel set such that for each
$R \subseteq X^2$
is a Borel set such that for each
![]() $x \in X$
, the restriction of E to the set
$x \in X$
, the restriction of E to the set
is smooth, then there is a Borel injective homomorphism
![]() $\rho \colon \mathcal {C} \to X$
from
$\rho \colon \mathcal {C} \to X$
from
![]() $(\mathbb {E}_0^c,\, \mathbb {E}_0)$
to
$(\mathbb {E}_0^c,\, \mathbb {E}_0)$
to
![]() $(R^c,\, E)$
.
$(R^c,\, E)$
.
Here, given binary relations
![]() $(E_1, \ldots , E_n)$
on a set X and
$(E_1, \ldots , E_n)$
on a set X and
![]() $(F_1, \ldots , F_n)$
on a set Y, a homomorphism from
$(F_1, \ldots , F_n)$
on a set Y, a homomorphism from
![]() $(E_1, \ldots , E_n)$
to
$(E_1, \ldots , E_n)$
to
![]() $(F_1, \ldots , F_n)$
is a function
$(F_1, \ldots , F_n)$
is a function
![]() $\rho : X \to Y$
such that
$\rho : X \to Y$
such that
![]() $x\, E_i \, y \Rightarrow \rho (x)\, F_i\, \rho (y)$
for all x,
$x\, E_i \, y \Rightarrow \rho (x)\, F_i\, \rho (y)$
for all x,
![]() $y \in X$
and
$y \in X$
and
![]() $1 \leqslant i \leqslant n$
. We derive Lemma 3.10 from the
$1 \leqslant i \leqslant n$
. We derive Lemma 3.10 from the
![]() $\mathbb {E}_0$
-dichotomy and a Mycielski-style theorem due to Miller [Reference Miller, Babinkostova, Caicedo, Geschke and Scheepers14, Proposition 3]. We then argue that it can be applied with
$\mathbb {E}_0$
-dichotomy and a Mycielski-style theorem due to Miller [Reference Miller, Babinkostova, Caicedo, Geschke and Scheepers14, Proposition 3]. We then argue that it can be applied with
![]() $E= {\sim }$
and
$E= {\sim }$
and
resulting in a mapping
![]() $\rho \colon \mathcal {C} \to E(L)$
with the desired properties. The details are presented in Section 6.
$\rho \colon \mathcal {C} \to E(L)$
with the desired properties. The details are presented in Section 6.
4. Proof of Theorem 3.6
Theorem 3.6
If L is a Borel graph that is a line graph, then L has a Borel line graph relation.
Proof. Given e,
![]() $f \in E(L)$
, we write
$f \in E(L)$
, we write
![]() $e \star f$
whenever there exists a clique C in L with e,
$e \star f$
whenever there exists a clique C in L with e,
![]() $f \in E(C)$
. Note that the relation
$f \in E(C)$
. Note that the relation
![]() $\star $
is Borel, since
$\star $
is Borel, since
Let
![]() $\sim _L$
be an arbitrary (not necessarily Borel) line graph relation on L. Then
$\sim _L$
be an arbitrary (not necessarily Borel) line graph relation on L. Then
![]() ${\sim _L} \subseteq {\star }$
. Call an induced subgraph
${\sim _L} \subseteq {\star }$
. Call an induced subgraph
![]() $\Gamma \subseteq L$
nice if
$\Gamma \subseteq L$
nice if
![]() $\Gamma $
is connected, finite, and
$\Gamma $
is connected, finite, and
![]() $|V(\Gamma )|\geqslant 7$
. Note that if
$|V(\Gamma )|\geqslant 7$
. Note that if
![]() $\Gamma $
is a nice subgraph of L, then it is a nonsingular line graph, as it is an induced subgraph of L and all singular graphs have at most six vertices. Thus, by Corollary 3.9, every nice graph
$\Gamma $
is a nice subgraph of L, then it is a nonsingular line graph, as it is an induced subgraph of L and all singular graphs have at most six vertices. Thus, by Corollary 3.9, every nice graph
![]() $\Gamma $
has a unique line graph relation,
$\Gamma $
has a unique line graph relation,
![]() $\sim _{\Gamma }$
. By Lemma 3.4,
$\sim _{\Gamma }$
. By Lemma 3.4,
![]() ${\sim _L}|_\Gamma $
is also a line graph relation on
${\sim _L}|_\Gamma $
is also a line graph relation on
![]() $\Gamma $
, and thus
$\Gamma $
, and thus
![]() ${\sim _\Gamma } = {{\sim _L}|_\Gamma }$
.
${\sim _\Gamma } = {{\sim _L}|_\Gamma }$
.
Define relations
![]() $R_1$
and
$R_1$
and
![]() $R_2$
on
$R_2$
on
![]() $E(L)$
as follows:
$E(L)$
as follows:
 $$ \begin{align*} e \,R_1\, f &\iff \exists \text{ nice } \Gamma \subseteq \text{ L with } e, f \in E(\Gamma) \text{ and } e \sim_{\Gamma} f.\\ e \,R_2\, f &\iff e \star f \text{ and } \forall \text{ nice } \Gamma \subseteq L \left(e, f \in E(\Gamma) \Rightarrow e \sim_{\Gamma} f\right). \end{align*} $$
$$ \begin{align*} e \,R_1\, f &\iff \exists \text{ nice } \Gamma \subseteq \text{ L with } e, f \in E(\Gamma) \text{ and } e \sim_{\Gamma} f.\\ e \,R_2\, f &\iff e \star f \text{ and } \forall \text{ nice } \Gamma \subseteq L \left(e, f \in E(\Gamma) \Rightarrow e \sim_{\Gamma} f\right). \end{align*} $$
Claim 4.1. The relations
![]() $R_1$
and
$R_1$
and
![]() $R_2$
have the following properties
$R_2$
have the following properties
![]() $:$
$:$
-
(i)
 $R_1 \subseteq R_2 \subseteq {\star }$
,
$R_1 \subseteq R_2 \subseteq {\star }$
, -
(ii) if H is an infinite component of L, then
 $R_1|_H =\, R_2|_H = {\sim _{L}}|_H$
,
$R_1|_H =\, R_2|_H = {\sim _{L}}|_H$
, -
(iii)
 $R_1$
is analytic, while
$R_1$
is analytic, while
 $R_2$
is coanalytic.
$R_2$
is coanalytic.
Proof. We start by observing that if edges e,
![]() $f \in E(L)$
are contained in some nice graph, then
$f \in E(L)$
are contained in some nice graph, then
because
![]() ${\sim _\Gamma } = {{\sim _L}|_\Gamma }$
for every nice graph
${\sim _\Gamma } = {{\sim _L}|_\Gamma }$
for every nice graph
![]() $\Gamma $
and
$\Gamma $
and
![]() ${\sim _L} \subseteq {\star }$
.
${\sim _L} \subseteq {\star }$
.
(i) The inclusion
![]() $R_2 \subseteq {\star }$
is clear, while
$R_2 \subseteq {\star }$
is clear, while
![]() $R_1 \subseteq R_2$
follows by (4.1).
$R_1 \subseteq R_2$
follows by (4.1).
(ii) If H is an infinite component of L, then for any pair of edges e,
![]() $f \in E(H)$
we can find a nice subgraph of H containing both e and f, so
$f \in E(H)$
we can find a nice subgraph of H containing both e and f, so
![]() $R_1|_H =\, R_2|_H = {\sim _{L}}|_H$
by (4.1).
$R_1|_H =\, R_2|_H = {\sim _{L}}|_H$
by (4.1).
(iii) For each
![]() $n \in {\mathbb {N}}$
, let
$n \in {\mathbb {N}}$
, let

The statement “the graph ![]() is nice, e,
is nice, e,
![]() $f \in E(\Gamma )$
, and
$f \in E(\Gamma )$
, and
![]() $e \sim _\Gamma f$
” can be expressed as a Boolean combination of statements of the form “
$e \sim _\Gamma f$
” can be expressed as a Boolean combination of statements of the form “
![]() $v_i = v_j$
,” “
$v_i = v_j$
,” “
![]() $v_i v_j \in E(L)$
,” “
$v_i v_j \in E(L)$
,” “
![]() $e = \{v_i, v_j\}$
,” and “
$e = \{v_i, v_j\}$
,” and “
![]() $f = \{v_i, v_j\}$
.” It follows that the set
$f = \{v_i, v_j\}$
.” It follows that the set
![]() $P_n$
is Borel. By definition,
$P_n$
is Borel. By definition,
which shows that
![]() $R_1$
is a countable union of analytic sets, hence it is itself analytic. The proof that
$R_1$
is a countable union of analytic sets, hence it is itself analytic. The proof that
![]() $R_2$
is coanalytic is similar, so we omit the details.
$R_2$
is coanalytic is similar, so we omit the details.
By Claim 4.1 and the analytic separation theorem, there exists a Borel set
![]() ${R \subseteq E(L)^2}$
such that
${R \subseteq E(L)^2}$
such that
![]() $R_1 \subseteq R \subseteq R_2$
. Let
$R_1 \subseteq R \subseteq R_2$
. Let
![]() $\equiv $
be the equivalence relation on
$\equiv $
be the equivalence relation on
![]() $V(L)$
whose classes are the components of L. Note that
$V(L)$
whose classes are the components of L. Note that
![]() $\equiv $
is analytic (see Example 2.3). For a vertex
$\equiv $
is analytic (see Example 2.3). For a vertex
![]() $x \in V(L)$
, let
$x \in V(L)$
, let
![]() $[x]$
denote the component of L containing x, and define:
$[x]$
denote the component of L containing x, and define:

Claim 4.2.
![]() $A_1$
and
$A_1$
and
![]() $A_2$
are disjoint analytic
$A_2$
are disjoint analytic
![]() $\equiv $
-invariant sets.
$\equiv $
-invariant sets.
Proof. That
![]() $A_1$
and
$A_1$
and
![]() $A_2$
are
$A_2$
are
![]() $\equiv $
-invariant is immediate from the way they are defined. Next, we write
$\equiv $
-invariant is immediate from the way they are defined. Next, we write
 $$\begin{align*}&x \in A_1 \\&\quad{\iff}\kern1.3pt \forall\, n \in {\mathbb{N}},\, \exists\, y_1, \dots, y_n \in V(L) \, \big(y_1, \, \ldots, \, y_n \text{ are distinct and } \forall i \in [n] \, (x \kern1.3pt{\equiv}\kern1.3pt y_i)\kern-0.2pt\big), \end{align*}$$
$$\begin{align*}&x \in A_1 \\&\quad{\iff}\kern1.3pt \forall\, n \in {\mathbb{N}},\, \exists\, y_1, \dots, y_n \in V(L) \, \big(y_1, \, \ldots, \, y_n \text{ are distinct and } \forall i \in [n] \, (x \kern1.3pt{\equiv}\kern1.3pt y_i)\kern-0.2pt\big), \end{align*}$$
which shows that
![]() $A_1$
is a countable intersection of analytic sets, so it is itself analytic. To see that
$A_1$
is a countable intersection of analytic sets, so it is itself analytic. To see that
![]() $A_2$
is analytic, recall that by Lemma 3.3,
$A_2$
is analytic, recall that by Lemma 3.3,
![]() $R|_{[x]}$
is a line graph relation if and only if:
$R|_{[x]}$
is a line graph relation if and only if:
-
(1)
 $R|_{[x]}$
is an equivalence relation,
$R|_{[x]}$
is an equivalence relation, -
(2) each equivalence class of
 $R|_{[x]}$
is the edge set of a clique in
$R|_{[x]}$
is the edge set of a clique in
 $[x]$
, and
$[x]$
, and -
(3) for each vertex
 $y \equiv x$
, y is incident to at most two equivalence classes of
$y \equiv x$
, y is incident to at most two equivalence classes of
 $R|_{[x]}$
.
$R|_{[x]}$
.
For the first condition, we have
 $$ \begin{align*} (1) \kern1.4pt{\iff}\kern1.4pt \forall\, e, f, g \in E([x])\, \bigg(&\, e \, R \, e,\ e \, R \, f \Rightarrow f \, R \, e,\ \Big(e \, R \, f \text{ and }f \, R \, g \Big)\, {\Rightarrow}\, e \, R \, g \bigg). \end{align*} $$
$$ \begin{align*} (1) \kern1.4pt{\iff}\kern1.4pt \forall\, e, f, g \in E([x])\, \bigg(&\, e \, R \, e,\ e \, R \, f \Rightarrow f \, R \, e,\ \Big(e \, R \, f \text{ and }f \, R \, g \Big)\, {\Rightarrow}\, e \, R \, g \bigg). \end{align*} $$
For the second condition, assuming (1) holds, we have
 $$ \begin{align*} (2) \iff \forall\, e &= \{a,b\},\\ f &= \{c,d\} \kern1.3pt{\in}\kern1.3pt E([x]) \, \bigg(\kern-1pt e \, R \, f \kern1.4pt{\Rightarrow}\kern1.4pt \Big(a = c \text{ or } \big(\{a,c\} \in E(L), \, \{a,c\} \,R\, e \big) \Big) \!\bigg). \end{align*} $$
$$ \begin{align*} (2) \iff \forall\, e &= \{a,b\},\\ f &= \{c,d\} \kern1.3pt{\in}\kern1.3pt E([x]) \, \bigg(\kern-1pt e \, R \, f \kern1.4pt{\Rightarrow}\kern1.4pt \Big(a = c \text{ or } \big(\{a,c\} \in E(L), \, \{a,c\} \,R\, e \big) \Big) \!\bigg). \end{align*} $$
For the third condition, assuming (1) holds, we have
 $$ \begin{align*} (3) \iff \lnot \Bigg( \exists\, y \equiv x,\, \exists\, e, f, g \in E([x])\, \Big(y \in e \cap f\cap g,\, e \, R^c \, f,\, e \, R^c \, g,\, f \, R^c \, g \Big)\Bigg). \end{align*} $$
$$ \begin{align*} (3) \iff \lnot \Bigg( \exists\, y \equiv x,\, \exists\, e, f, g \in E([x])\, \Big(y \in e \cap f\cap g,\, e \, R^c \, f,\, e \, R^c \, g,\, f \, R^c \, g \Big)\Bigg). \end{align*} $$
Since R is Borel and the relation
is analytic, these three conditions define coanalytic sets, and thus
![]() $A_2$
is analytic.
$A_2$
is analytic.
Finally, to see that
![]() $A_1$
and
$A_1$
and
![]() $A_2$
are disjoint, let H be an infinite component of L. By Claim 4.1,
$A_2$
are disjoint, let H be an infinite component of L. By Claim 4.1,
![]() $R_1|_H =\, R_2|_H = {\sim _{L}}|_H$
. Since
$R_1|_H =\, R_2|_H = {\sim _{L}}|_H$
. Since
![]() $R_1 \subseteq R \subseteq R_2$
, it follows that
$R_1 \subseteq R \subseteq R_2$
, it follows that
![]() $R|_H = {\sim _{L}}|_H$
. In particular,
$R|_H = {\sim _{L}}|_H$
. In particular,
![]() $R|_H$
is a line graph relation on H, so H is contained in
$R|_H$
is a line graph relation on H, so H is contained in
![]() $A_2^c$
, as desired.
$A_2^c$
, as desired.
By Claim 4.2, we may apply invariant analytic separation (Lemma 2.7) with
![]() ${X = V(L)}$
,
${X = V(L)}$
,
![]() $E = {\equiv }$
,
$E = {\equiv }$
,
![]() $Y = A_1$
, and
$Y = A_1$
, and
![]() $Z = A_2$
to obtain a Borel
$Z = A_2$
to obtain a Borel
![]() ${\equiv }$
-invariant set
${\equiv }$
-invariant set
![]() $B \subseteq V(L)$
such that
$B \subseteq V(L)$
such that
![]() $A_1 \subseteq B \subseteq A_2^c$
. Since
$A_1 \subseteq B \subseteq A_2^c$
. Since
![]() $B \subseteq A_2^c$
, it follows that
$B \subseteq A_2^c$
, it follows that
![]() $R|_{B}$
is a Borel line graph relation on
$R|_{B}$
is a Borel line graph relation on
![]() $L[B]$
. On the other hand, since
$L[B]$
. On the other hand, since
![]() $A_1 \subseteq B$
, every component of
$A_1 \subseteq B$
, every component of
![]() $L[B^c]$
is finite. This means that we may employ the Luzin–Novikov theorem to pick, in a Borel way, a single line graph relation on each component of
$L[B^c]$
is finite. This means that we may employ the Luzin–Novikov theorem to pick, in a Borel way, a single line graph relation on each component of
![]() $L[B^c]$
and form a Borel line graph relation
$L[B^c]$
and form a Borel line graph relation
![]() $R^*$
on
$R^*$
on
![]() $L[B^c]$
. (Since arguments dealing with Borel graphs with finite components in this manner are standard, we defer the details to Appendix 7.2.) As B is
$L[B^c]$
. (Since arguments dealing with Borel graphs with finite components in this manner are standard, we defer the details to Appendix 7.2.) As B is
![]() $\equiv $
-invariant, we conclude that
$\equiv $
-invariant, we conclude that
![]() $R|_{L[B]} \cup R^*$
is a desired Borel line graph relation on L.
$R|_{L[B]} \cup R^*$
is a desired Borel line graph relation on L.
5. Proof of Theorem 3.7, (2)
 $\Rightarrow $
(1)
$\Rightarrow $
(1)
Theorem 3.7, (2)
 $\Rightarrow $
(1)
$\Rightarrow $
(1)
Let L be a Borel graph that is a line graph. If L has a smooth line graph relation
![]() $\sim $
, then L is a Borel line graph.
$\sim $
, then L is a Borel line graph.
Proof. Let
![]() $f : E(L) \to \mathbb {R}$
witness the smoothness of
$f : E(L) \to \mathbb {R}$
witness the smoothness of
![]() $\sim $
. Define R,
$\sim $
. Define R,
![]() $R' \subseteq V(L) \times \mathbb {R}$
by
$R' \subseteq V(L) \times \mathbb {R}$
by
 $$ \begin{align*} v\,R\,x \iff \exists\, uw &\in E(L)\, \big(f(uw) = x \text{ and } (v = u \text{ or } v = w)\big),\\ v\,R'\,x \iff \forall\, uw &\in E(L) \, \Big(f(uw) = x \Rightarrow \\ &\hspace{-5pt}\big((vu \in E(L),\, f(vu) = x) \text{ or } (vw \in E(L),\, f(vw) = x)\big)\Big). \end{align*} $$
$$ \begin{align*} v\,R\,x \iff \exists\, uw &\in E(L)\, \big(f(uw) = x \text{ and } (v = u \text{ or } v = w)\big),\\ v\,R'\,x \iff \forall\, uw &\in E(L) \, \Big(f(uw) = x \Rightarrow \\ &\hspace{-5pt}\big((vu \in E(L),\, f(vu) = x) \text{ or } (vw \in E(L),\, f(vw) = x)\big)\Big). \end{align*} $$
Note that
![]() $R \subseteq R'$
and
$R \subseteq R'$
and
![]() $R' \setminus R = \{(v,x) \in V(L) \times \mathbb {R} \,:\, x \notin \mathrm {im}(f)\}$
. Since f is Borel, it follows that R is analytic and
$R' \setminus R = \{(v,x) \in V(L) \times \mathbb {R} \,:\, x \notin \mathrm {im}(f)\}$
. Since f is Borel, it follows that R is analytic and
![]() $R'$
is coanalytic.
$R'$
is coanalytic.
As
![]() $R \subseteq R'$
, analytic separation yields a Borel set
$R \subseteq R'$
, analytic separation yields a Borel set
![]() $R_0$
such that
$R_0$
such that
![]() $R \subseteq R_0 \subseteq R'$
. Define
$R \subseteq R_0 \subseteq R'$
. Define
![]() $B_0 \subseteq R_0$
by
$B_0 \subseteq R_0$
by
Since
![]() $R_0$
is Borel,
$R_0$
is Borel,
![]() $B_0$
is analytic. Note that if
$B_0$
is analytic. Note that if
![]() $(v,z) \in R$
, then
$(v,z) \in R$
, then
![]() $z \in \mathrm {im}(f)$
, so if u is a neighbor of v such that
$z \in \mathrm {im}(f)$
, so if u is a neighbor of v such that
![]() $(u,z) \in R_0$
, then
$(u,z) \in R_0$
, then
![]() $(u,z) \in R$
as well. Thus both u and v are incident to edges that are mapped by f to z. Since
$(u,z) \in R$
as well. Thus both u and v are incident to edges that are mapped by f to z. Since
![]() $f^{-1}(z)$
is the edge set of a clique, it follows that
$f^{-1}(z)$
is the edge set of a clique, it follows that
![]() $f(uv) = z$
for all such u, so
$f(uv) = z$
for all such u, so
![]() $(v,z) \notin B_0$
. In other words,
$(v,z) \notin B_0$
. In other words,
![]() $R \cap B_0 = \emptyset $
.
$R \cap B_0 = \emptyset $
.
By analytic separation, there is a Borel set
![]() $R_1$
with
$R_1$
with
![]() $R \subseteq R_1 \subseteq R_0 \setminus B_0$
. Define
$R \subseteq R_1 \subseteq R_0 \setminus B_0$
. Define
![]() $B_1 \subseteq R_1$
by
$B_1 \subseteq R_1$
by
Again,
![]() $B_1$
is analytic. Moreover, for each
$B_1$
is analytic. Moreover, for each
![]() $z \in \mathrm {im}(f)$
, the vertices of L to which z is R-related form a clique, so
$z \in \mathrm {im}(f)$
, the vertices of L to which z is R-related form a clique, so
![]() $R \cap B_1 = \emptyset $
. Thus, by analytic separation, there is a Borel set
$R \cap B_1 = \emptyset $
. Thus, by analytic separation, there is a Borel set
![]() $R_2$
with
$R_2$
with
![]() $R \subseteq R_2 \subseteq R_1 \setminus B_1$
.
$R \subseteq R_2 \subseteq R_1 \setminus B_1$
.
Next we define a subset
![]() $B_2 \subseteq R_2$
by
$B_2 \subseteq R_2$
by
Since
![]() $R_2$
is Borel and R is analytic,
$R_2$
is Borel and R is analytic,
![]() $B_2$
is analytic. Furthermore, each vertex of L can be R-related to at most two elements of
$B_2$
is analytic. Furthermore, each vertex of L can be R-related to at most two elements of
![]() $\mathbb {R}$
, so
$\mathbb {R}$
, so
![]() $R \cap B_2 = \emptyset $
. By analytic separation, there exists a Borel set
$R \cap B_2 = \emptyset $
. By analytic separation, there exists a Borel set
![]() $R_3$
with
$R_3$
with
![]() $R \subseteq R_3 \subseteq R_2\setminus B_2$
. Let
$R \subseteq R_3 \subseteq R_2\setminus B_2$
. Let
![]() $B_3 \subseteq R_3$
be defined as follows:
$B_3 \subseteq R_3$
be defined as follows:
Since
![]() $R_3$
is Borel and R is analytic,
$R_3$
is Borel and R is analytic,
![]() $B_3$
is analytic. Take any
$B_3$
is analytic. Take any
![]() $(v,z) \in B_3$
with
$(v,z) \in B_3$
with
![]() ${(v,x) \in R}$
,
${(v,x) \in R}$
,
![]() $(v,y) \in R_3$
, and
$(v,y) \in R_3$
, and
![]() $|\{x, y, z\}| = 3$
. If
$|\{x, y, z\}| = 3$
. If
![]() $(v,z) \in R$
, then
$(v,z) \in R$
, then
![]() $(v,y) \in B_2$
, and thus
$(v,y) \in B_2$
, and thus
![]() $(v,y) \notin R_3$
, which is a contradiction. Thus,
$(v,y) \notin R_3$
, which is a contradiction. Thus,
![]() $R \cap B_3 = \emptyset $
. By analytic separation, there is a Borel set
$R \cap B_3 = \emptyset $
. By analytic separation, there is a Borel set
![]() $R_4$
with
$R_4$
with
![]() $R \subseteq R_4 \subseteq R_3\setminus B_3$
. Let
$R \subseteq R_4 \subseteq R_3\setminus B_3$
. Let
Since
![]() $R_4$
is Borel,
$R_4$
is Borel,
![]() $B_4$
is analytic. If
$B_4$
is analytic. If
![]() $(v,z) \in B_4$
with
$(v,z) \in B_4$
with
![]() $(v,x) \in R_4$
,
$(v,x) \in R_4$
,
![]() $(v,y) \in R_4$
, and
$(v,y) \in R_4$
, and
![]() $|\{x, y, z\}| = 3$
, and
$|\{x, y, z\}| = 3$
, and
![]() $(v,z) \in R$
, then
$(v,z) \in R$
, then
![]() $(v,x) \in B_3$
, which is impossible. Therefore,
$(v,x) \in B_3$
, which is impossible. Therefore,
![]() $R \cap B_4 = \emptyset $
.
$R \cap B_4 = \emptyset $
.
Finally, analytic separation yields a Borel set
![]() $R_5$
with
$R_5$
with
![]() $R \subseteq R_5 \subseteq R_4\setminus B_4$
. Observe that
$R \subseteq R_5 \subseteq R_4\setminus B_4$
. Observe that
![]() $R_5$
has the following properties:
$R_5$
has the following properties:
-
(i)
 $R \subseteq R_5 \subseteq R'$
.
$R \subseteq R_5 \subseteq R'$
.
This is clear from the construction.
-
(ii) Every vertex of
 $L\ R_5$
-relates to at most two elements of
$L\ R_5$
-relates to at most two elements of
 $\mathbb {R}$
.
$\mathbb {R}$
.
This follows since
![]() $R_5 \cap B_4 = \emptyset $
.
$R_5 \cap B_4 = \emptyset $
.
-
(iii) Every element of
 $\mathbb {R} \setminus \mathrm {im}(f)\ R_5$
-relates to at most one vertex of L.
$\mathbb {R} \setminus \mathrm {im}(f)\ R_5$
-relates to at most one vertex of L.
Indeed, suppose
![]() $z \in \mathbb {R}\ R_5$
-relates to two different vertices u,
$z \in \mathbb {R}\ R_5$
-relates to two different vertices u,
![]() $v \in V(L)$
. Since
$v \in V(L)$
. Since
![]() ${R_5 \cap B_1 = \emptyset} $
, it follows that
${R_5 \cap B_1 = \emptyset} $
, it follows that
![]() $uv \in E(L)$
. Then, since
$uv \in E(L)$
. Then, since
![]() $R_5 \cap B_0 = \emptyset $
, we have
$R_5 \cap B_0 = \emptyset $
, we have
![]() $f(uv) = z$
, i.e.,
$f(uv) = z$
, i.e.,
![]() $z \in \mathrm {im}(f)$
, as claimed.
$z \in \mathrm {im}(f)$
, as claimed.
Having found a Borel relation
![]() $R_5$
satisfying conditions (i)–(iii), we can now define a Borel graph G such that
$R_5$
satisfying conditions (i)–(iii), we can now define a Borel graph G such that
![]() $L(G) \cong _B L$
. To this end, let
$L(G) \cong _B L$
. To this end, let

As
![]() $R_5$
is Borel, the Luzin–Novikov theorem together with property (ii) of
$R_5$
is Borel, the Luzin–Novikov theorem together with property (ii) of
![]() $R_5$
shows that
$R_5$
shows that
![]() $V_0$
and
$V_0$
and
![]() $V_2$
are Borel sets, and thus
$V_2$
are Borel sets, and thus
![]() $V_1$
is Borel as well. Without loss of generality (e.g., by replacing
$V_1$
is Borel as well. Without loss of generality (e.g., by replacing
![]() $V(L)$
with
$V(L)$
with
![]() $\{2\} \times V(L)$
), we may assume that the sets
$\{2\} \times V(L)$
), we may assume that the sets
![]() $\mathbb {R}$
,
$\mathbb {R}$
,
![]() $V(L)$
, and
$V(L)$
, and
![]() $\{0,1\}\times V(L)$
are disjoint. We then construct G as follows:
$\{0,1\}\times V(L)$
are disjoint. We then construct G as follows:
where

This construction is illustrated in Figure 3. To see that G is a Borel graph, we need to verify that the sets
![]() $E_0$
,
$E_0$
,
![]() $E_1$
, and
$E_1$
, and
![]() $E_2$
are Borel. For
$E_2$
are Borel. For
![]() $E_0$
and
$E_0$
and
![]() $E_1$
, this is clear. For
$E_1$
, this is clear. For
![]() $E_2$
, notice that if x,
$E_2$
, notice that if x,
![]() $y \in \mathrm {im}(f)$
are distinct, then there is at most one vertex
$y \in \mathrm {im}(f)$
are distinct, then there is at most one vertex
![]() $v \in V_2$
such that
$v \in V_2$
such that
![]() $(v,x)$
,
$(v,x)$
,
![]() $(v,y) \in R_5$
, namely the common vertex of the cliques
$(v,y) \in R_5$
, namely the common vertex of the cliques
![]() $f^{-1}(x)$
and
$f^{-1}(x)$
and
![]() $f^{-1}(y)$
. On the other hand, if, say,
$f^{-1}(y)$
. On the other hand, if, say,
![]() $x \in \mathbb {R} \setminus \mathrm {im}(f)$
, then by (iii), there is at most one vertex v such that
$x \in \mathbb {R} \setminus \mathrm {im}(f)$
, then by (iii), there is at most one vertex v such that
![]() $(v,x) \in R_5$
. In either case, there is at most one vertex v with
$(v,x) \in R_5$
. In either case, there is at most one vertex v with
![]() $(v,x)$
,
$(v,x)$
,
![]() $(v,y) \in R_5$
and hence, by the Luzin–Novikov theorem, the set
$(v,y) \in R_5$
and hence, by the Luzin–Novikov theorem, the set
![]() $E_2$
is Borel.
$E_2$
is Borel.

Figure 3 The construction of G using the relation
![]() $R_5$
. Here the dashed edges represent the relation R and the dotted ones represent the relation
$R_5$
. Here the dashed edges represent the relation R and the dotted ones represent the relation
![]() $R_5 \setminus R$
. In this example,
$R_5 \setminus R$
. In this example,
![]() $V_0 = \{v_8\}$
,
$V_0 = \{v_8\}$
,
![]() $V_1 = \{v_1, v_2, v_4, v_9\}$
, and
$V_1 = \{v_1, v_2, v_4, v_9\}$
, and
![]() $V_2 = \{v_3, v_5, v_6, v_7\}$
.
$V_2 = \{v_3, v_5, v_6, v_7\}$
.
To argue that
![]() $L \cong _B L(G)$
, we define a Borel isomorphism
$L \cong _B L(G)$
, we define a Borel isomorphism
![]() $\varphi $
from
$\varphi $
from
![]() $L(G)$
to L as follows. For
$L(G)$
to L as follows. For
![]() $\{(0,v), (1, v)\} \in E_0$
, let
$\{(0,v), (1, v)\} \in E_0$
, let ![]() , for
, for
![]() $\{v,x\} \in E_1$
, define
$\{v,x\} \in E_1$
, define ![]() , and for
, and for
![]() $\{x,y\} \in E_2$
, let
$\{x,y\} \in E_2$
, let
![]() $\varphi (\{x,y\})$
be the unique
$\varphi (\{x,y\})$
be the unique
![]() $v \in V_2$
such that
$v \in V_2$
such that
![]() $(v,x)$
,
$(v,x)$
,
![]() $(v,y) \in R_5$
. It is immediate from the definition that
$(v,y) \in R_5$
. It is immediate from the definition that
![]() $\varphi $
is indeed a desired Borel isomorphism.
$\varphi $
is indeed a desired Borel isomorphism.
6. Finishing the proof
Recall that a subset of a topological space is meager if it is a union of countably many nowhere dense sets. We shall use the following result of Miller [Reference Miller, Babinkostova, Caicedo, Geschke and Scheepers14]:
Theorem 6.1 (Miller [Reference Miller, Babinkostova, Caicedo, Geschke and Scheepers14, Proposition 3])
Let
![]() $R \subseteq \mathcal {C}^2$
be a meager set. Then there exists a continuous injective homomorphism
$R \subseteq \mathcal {C}^2$
be a meager set. Then there exists a continuous injective homomorphism
![]() $\rho : \mathcal {C} \to \mathcal {C}$
from
$\rho : \mathcal {C} \to \mathcal {C}$
from
![]() $(\mathbb {E}_0^c,\, \mathbb {E}_0)$
to
$(\mathbb {E}_0^c,\, \mathbb {E}_0)$
to
![]() $(R^c,\, \mathbb {E}_0)$
.
$(R^c,\, \mathbb {E}_0)$
.
With Theorem 6.1 in hand, we can prove Lemma 3.10:
Lemma 3.10
Let X be a standard Borel space and let
![]() $E \subseteq X^2$
be a nonsmooth Borel equivalence relation on X. If
$E \subseteq X^2$
be a nonsmooth Borel equivalence relation on X. If
![]() $R \subseteq X^2$
is a Borel set such that for each
$R \subseteq X^2$
is a Borel set such that for each
![]() $x \in X$
, the restriction of E to the set
$x \in X$
, the restriction of E to the set
is smooth, then there is a Borel injective homomorphism
![]() $\rho \colon \mathcal {C} \to X$
from
$\rho \colon \mathcal {C} \to X$
from
![]() $(\mathbb {E}_0^c,\, \mathbb {E}_0)$
to
$(\mathbb {E}_0^c,\, \mathbb {E}_0)$
to
![]() $(R^c,\, E)$
.
$(R^c,\, E)$
.
Proof. By the
![]() $\mathbb {E}_0$
-dichotomy, there is a Borel embedding
$\mathbb {E}_0$
-dichotomy, there is a Borel embedding
![]() $f \colon \mathcal {C} \to X$
from
$f \colon \mathcal {C} \to X$
from
![]() $\mathbb {E}_0$
to E. Since f is injective, its image is Borel, so we may, without loss of generality, replace X by
$\mathbb {E}_0$
to E. Since f is injective, its image is Borel, so we may, without loss of generality, replace X by
![]() $\mathrm {im}(f)$
and assume that f is a bijection. (For each
$\mathrm {im}(f)$
and assume that f is a bijection. (For each
![]() $x \in X$
, the restriction of E to
$x \in X$
, the restriction of E to
![]() $R(x) \cap \mathrm {im}(f) \subseteq R(x)$
remains smooth, so the assumptions of the lemma are still satisfied.) Since Borel bijections between standard Borel spaces are isomorphisms [Reference Kechris8, Corollary 15.2], we may in fact assume that
$R(x) \cap \mathrm {im}(f) \subseteq R(x)$
remains smooth, so the assumptions of the lemma are still satisfied.) Since Borel bijections between standard Borel spaces are isomorphisms [Reference Kechris8, Corollary 15.2], we may in fact assume that
![]() $X = \mathcal {C}$
, f is the identity map, and
$X = \mathcal {C}$
, f is the identity map, and
![]() $E = \mathbb {E}_0$
. If
$E = \mathbb {E}_0$
. If
![]() $A \subseteq \mathcal {C}$
is a Borel set such that
$A \subseteq \mathcal {C}$
is a Borel set such that
![]() $\mathbb {E}_0|_A$
is smooth, then A is meager [Reference Uzcátegui A19, Corollary 4.12], so
$\mathbb {E}_0|_A$
is smooth, then A is meager [Reference Uzcátegui A19, Corollary 4.12], so
![]() $R(x)$
is meager for all
$R(x)$
is meager for all
![]() $x \in \mathcal {C}$
. By the Kuratowski–Ulam theorem [Reference Kechris8, Theorem 8.41], it follows that R is a meager subset of
$x \in \mathcal {C}$
. By the Kuratowski–Ulam theorem [Reference Kechris8, Theorem 8.41], it follows that R is a meager subset of
![]() $\mathcal {C}^2$
. Therefore, we may apply Theorem 6.1 to get a continuous (hence Borel) injective homomorphism
$\mathcal {C}^2$
. Therefore, we may apply Theorem 6.1 to get a continuous (hence Borel) injective homomorphism
![]() $\rho : \mathcal {C} \to \mathcal {C}$
from
$\rho : \mathcal {C} \to \mathcal {C}$
from
![]() $(\mathbb {E}_0^c,\, \mathbb {E}_0)$
to
$(\mathbb {E}_0^c,\, \mathbb {E}_0)$
to
![]() $(R^c,\, \mathbb {E}_0)$
, as desired.
$(R^c,\, \mathbb {E}_0)$
, as desired.
Now we have all the necessary ingredients to complete the proof of our main result.
Lemma 3.5
Let L be a Borel graph that is a line graph. Then L is a Borel line graph if and only if L does not contain a Borel copy of
![]() $\mathbb {K}_0$
.
$\mathbb {K}_0$
.
Proof. By Theorem 3.6, there is a Borel line graph relation
![]() $\sim $
on L. If
$\sim $
on L. If
![]() $\sim $
is smooth, then L is a Borel line graph by Theorem 3.7, and thus contains no Borel copies of
$\sim $
is smooth, then L is a Borel line graph by Theorem 3.7, and thus contains no Borel copies of
![]() $\mathbb {K}_0$
. Now suppose that
$\mathbb {K}_0$
. Now suppose that
![]() $\sim $
is nonsmooth. Our goal is to show that L contains a Borel copy of
$\sim $
is nonsmooth. Our goal is to show that L contains a Borel copy of
![]() $\mathbb {K}_0$
.
$\mathbb {K}_0$
.
As
![]() $\sim $
is Borel, every
$\sim $
is Borel, every
![]() $\sim $
-class is a Borel subset of
$\sim $
-class is a Borel subset of
![]() $E(L)$
. For a
$E(L)$
. For a
![]() $\sim $
-class C, let
$\sim $
-class C, let
![]() $V(C) \subseteq V(L)$
be the set of all vertices incident to an edge in C. The set
$V(C) \subseteq V(L)$
be the set of all vertices incident to an edge in C. The set
![]() $V(C)$
is Borel since, fixing an arbitrary edge
$V(C)$
is Borel since, fixing an arbitrary edge
![]() $e \in C$
and a vertex
$e \in C$
and a vertex
![]() $x \in e$
, we can write
$x \in e$
, we can write
For an edge
![]() $e \in E(L)$
, let
$e \in E(L)$
, let
![]() $C_{e}$
be the
$C_{e}$
be the
![]() $\sim $
-class containing e, and for each
$\sim $
-class containing e, and for each
![]() $\sim $
-class C, define
$\sim $
-class C, define
Claim 6.2. For each
![]() $\sim $
-class C,
$\sim $
-class C,
![]() $S(C)$
is a
$S(C)$
is a
![]() $\sim $
-invariant Borel set and the relation
$\sim $
-invariant Borel set and the relation
![]() ${\sim }|_{S(C)}$
is smooth.
${\sim }|_{S(C)}$
is smooth.
Proof. Fix a
![]() $\sim $
-class C. It is clear from the definition that
$\sim $
-class C. It is clear from the definition that
![]() $S(C)$
is
$S(C)$
is
![]() $\sim $
-invariant. Observe that
$\sim $
-invariant. Observe that
Since for
![]() $e \not \in C$
, there can be at most one vertex w in
$e \not \in C$
, there can be at most one vertex w in
![]() $V(C_e) \cap V(C)$
, the set
$V(C_e) \cap V(C)$
, the set
![]() $S(C)$
is Borel by the Luzin–Novikov theorem. Additionally, the following function
$S(C)$
is Borel by the Luzin–Novikov theorem. Additionally, the following function
![]() $f \colon S(C) \to V(C)$
is Borel:
$f \colon S(C) \to V(C)$
is Borel:
If e,
![]() $e' \in S(C)$
are
$e' \in S(C)$
are
![]() $\sim $
-equivalent, then
$\sim $
-equivalent, then
![]() $f(e) = f(e')$
by construction. Conversely, if
$f(e) = f(e')$
by construction. Conversely, if
, then e and
![]() $e'$
belong to the same
$e'$
belong to the same
![]() $\sim $
-class, namely the unique
$\sim $
-class, namely the unique
![]() $\sim $
-class other than C incident to w. In other words, f witnesses the smoothness of
$\sim $
-class other than C incident to w. In other words, f witnesses the smoothness of
![]() ${\sim }|_{S(C)}$
, as desired.
${\sim }|_{S(C)}$
, as desired.
Define a relation
![]() $R \subseteq E(L)^2$
as follows:
$R \subseteq E(L)^2$
as follows:
Claim 6.3. For each
![]() $xy \in E(L)$
, the restriction of
$xy \in E(L)$
, the restriction of
![]() $\sim $
to
$\sim $
to ![]() is smooth.
is smooth.
Proof. Fix an edge
![]() $xy \in E(L)$
and observe that
$xy \in E(L)$
and observe that
where
![]() $C_x$
and
$C_x$
and
![]() $C_y$
are the
$C_y$
are the
![]() $\sim $
-classes distinct from
$\sim $
-classes distinct from
![]() $C_{xy}$
containing x and y respectively (if x or y is incident to only one
$C_{xy}$
containing x and y respectively (if x or y is incident to only one
![]() $\sim $
-class, we let the corresponding set in (6.1) be empty). For each
$\sim $
-class, we let the corresponding set in (6.1) be empty). For each
![]() $t \in \{xy, x, y\}$
, let
$t \in \{xy, x, y\}$
, let
![]() $f_t \colon S(C_t) \to \mathbb {R}$
witness the smoothness of
$f_t \colon S(C_t) \to \mathbb {R}$
witness the smoothness of
![]() ${\sim }|_{S(C_t)}$
(such functions
${\sim }|_{S(C_t)}$
(such functions
![]() $f_t$
exist by Claim 6.2). Then the following map
$f_t$
exist by Claim 6.2). Then the following map
![]() $f \colon R(xy) \to \{0,1,2,3\} \times \mathbb {R}$
witnesses the smoothness of
$f \colon R(xy) \to \{0,1,2,3\} \times \mathbb {R}$
witnesses the smoothness of
![]() ${\sim }|_{R(xy)}$
:
${\sim }|_{R(xy)}$
:

With Claim 6.3 in hand, we may apply Lemma 3.10 to obtain a Borel injective homomorphism
![]() $\rho \colon \mathcal {C} \to E(L)$
from
$\rho \colon \mathcal {C} \to E(L)$
from
![]() $(\mathbb {E}_0^c,\, \mathbb {E}_0)$
to
$(\mathbb {E}_0^c,\, \mathbb {E}_0)$
to
![]() $(R^c,\, \sim )$
. Since
$(R^c,\, \sim )$
. Since
![]() $\rho $
is injective, its image
$\rho $
is injective, its image
![]() $\mathrm {im}(\rho )$
is a Borel subset of
$\mathrm {im}(\rho )$
is a Borel subset of
![]() $E(L)$
. Let
$E(L)$
. Let
![]() $U \subseteq V(L)$
be the set of all vertices incident to an edge in
$U \subseteq V(L)$
be the set of all vertices incident to an edge in
![]() $\mathrm {im}(\rho )$
. Since every
$\mathrm {im}(\rho )$
. Since every
![]() $\mathbb {E}_0$
-class is countable, each
$\mathbb {E}_0$
-class is countable, each
![]() $\sim $
-class contains countably many edges in
$\sim $
-class contains countably many edges in
![]() $\mathrm {im}(\rho )$
. As every vertex belongs to at most two
$\mathrm {im}(\rho )$
. As every vertex belongs to at most two
![]() $\sim $
-classes, it is incident to countably many edges in
$\sim $
-classes, it is incident to countably many edges in
![]() $\mathrm {im}(\rho )$
. It follows by the Luzin–Novikov theorem that the set U is Borel, and hence
$\mathrm {im}(\rho )$
. It follows by the Luzin–Novikov theorem that the set U is Borel, and hence ![]() is a Borel induced subgraph of L.
is a Borel induced subgraph of L.
Observe that if
![]() $xy$
,
$xy$
,
![]() $yz \in E(H)$
, then
$yz \in E(H)$
, then
![]() $xy \sim yz$
. Indeed, let
$xy \sim yz$
. Indeed, let
![]() $\alpha $
,
$\alpha $
,
![]() $\beta $
,
$\beta $
,
![]() $\gamma \in \mathcal {C}$
be such that the edges
$\gamma \in \mathcal {C}$
be such that the edges
![]() $\rho (\alpha )$
,
$\rho (\alpha )$
,
![]() $\rho (\beta )$
, and
$\rho (\beta )$
, and
![]() $\rho (\gamma )$
are incident to x, y, and z respectively. Then
$\rho (\gamma )$
are incident to x, y, and z respectively. Then
![]() $\rho (\alpha ) \,R\, \rho (\beta ) \,R\, \rho (\gamma )$
, and thus
$\rho (\alpha ) \,R\, \rho (\beta ) \,R\, \rho (\gamma )$
, and thus
![]() $\alpha \,\mathbb {E}_0\, \beta \, \mathbb {E}_0 \, \gamma $
because
$\alpha \,\mathbb {E}_0\, \beta \, \mathbb {E}_0 \, \gamma $
because
![]() $\rho $
is a homomorphism from
$\rho $
is a homomorphism from
![]() $\mathbb {E}_0^c$
to
$\mathbb {E}_0^c$
to
![]() $R^c$
. Since
$R^c$
. Since
![]() $\rho $
is a homomorphism from
$\rho $
is a homomorphism from
![]() $\mathbb {E}_0$
to
$\mathbb {E}_0$
to
![]() $\sim $
, we conclude that
$\sim $
, we conclude that
![]() $\rho (\alpha ) \sim \rho (\beta ) \sim \rho (\gamma )$
. Therefore, x, y, and z are all incident to the same
$\rho (\alpha ) \sim \rho (\beta ) \sim \rho (\gamma )$
. Therefore, x, y, and z are all incident to the same
![]() $\sim $
-class, and thus
$\sim $
-class, and thus
![]() $xy \sim yz$
, as desired.
$xy \sim yz$
, as desired.
We conclude that the edge set of every component of H is contained in a single
![]() $\sim $
-class. Define the relation
$\sim $
-class. Define the relation
![]() ${\equiv _H}$
on
${\equiv _H}$
on
![]() $V(H)$
by
$V(H)$
by
Since H is locally countable,
![]() ${\equiv _H}$
is Borel by the Luzin–Novikov theorem (see Examples 2.3 and 2.5).
${\equiv _H}$
is Borel by the Luzin–Novikov theorem (see Examples 2.3 and 2.5).
Claim 6.4.
![]() ${\equiv _H}$
is nonsmooth.
${\equiv _H}$
is nonsmooth.
Proof. Suppose to the contrary that
![]() ${\equiv _H}$
is smooth, and let
${\equiv _H}$
is smooth, and let
![]() $f : V(H) \to \mathbb {R}$
witness the smoothness of
$f : V(H) \to \mathbb {R}$
witness the smoothness of
![]() ${\equiv _H}$
. Then
${\equiv _H}$
. Then
![]() $\xi : E(H) \to \mathbb {R}$
defined by
$\xi : E(H) \to \mathbb {R}$
defined by ![]() is well-defined and witnesses the smoothness of
is well-defined and witnesses the smoothness of
![]() ${\sim }|_H$
. But
${\sim }|_H$
. But
![]() ${\sim }|_H$
is nonsmooth as
${\sim }|_H$
is nonsmooth as
![]() $\rho $
is an embedding from
$\rho $
is an embedding from
![]() $\mathbb {E}_0$
to
$\mathbb {E}_0$
to
![]() ${\sim }|_H$
.
${\sim }|_H$
.
Since
![]() ${\equiv _H}$
is nonsmooth, by the
${\equiv _H}$
is nonsmooth, by the
![]() $\mathbb {E}_0$
-dichotomy there exists a Borel embedding
$\mathbb {E}_0$
-dichotomy there exists a Borel embedding
![]() $\varphi : \mathcal {C} \to V(H)$
from
$\varphi : \mathcal {C} \to V(H)$
from
![]() $\mathbb {E}_0$
to
$\mathbb {E}_0$
to
![]() ${\equiv _H}$
. As H is a union of disjoint cliques, it follows that
${\equiv _H}$
. As H is a union of disjoint cliques, it follows that
![]() $\varphi $
is a Borel isomorphism from
$\varphi $
is a Borel isomorphism from
![]() $\mathbb {K}_0$
to
$\mathbb {K}_0$
to
![]() $L[\mathrm {im}(\varphi )]$
. Therefore, L contains a Borel copy of
$L[\mathrm {im}(\varphi )]$
. Therefore, L contains a Borel copy of
![]() $\mathbb {K}_0$
, as desired.
$\mathbb {K}_0$
, as desired.
7. Appendices
7.1. Proof of Theorem 3.7, (2)
 $\Rightarrow $
(3)
$\Rightarrow $
(3)
As Corollary 3.9 implies two line graph relations differ only on singular components, which are all finite, the statement (2)
![]() $\Rightarrow $
(3) is an immediate corollary of the following lemma:
$\Rightarrow $
(3) is an immediate corollary of the following lemma:
Lemma 7.1. If E and
![]() $E'$
are Borel equivalence relations on a standard Borel space X such that E is smooth and every infinite
$E'$
are Borel equivalence relations on a standard Borel space X such that E is smooth and every infinite
![]() $E'$
-class is also an E-class, then
$E'$
-class is also an E-class, then
![]() $E'$
is smooth.
$E'$
is smooth.
Proof. Let
![]() $f : X \to \mathbb {R}$
witness the smoothness of E. Define the following subsets of X:
$f : X \to \mathbb {R}$
witness the smoothness of E. Define the following subsets of X:

Clearly
![]() $A_1$
is analytic and
$A_1$
is analytic and
![]() $A_2$
is coanalytic. Furthermore, if
$A_2$
is coanalytic. Furthermore, if
![]() $x \in A_1$
, then
$x \in A_1$
, then
![]() $[x]_{E'} = [x]_{E}$
, and thus
$[x]_{E'} = [x]_{E}$
, and thus
![]() $x \in A_2$
. So
$x \in A_2$
. So
![]() $A_1 \subseteq A_2$
. Since
$A_1 \subseteq A_2$
. Since
![]() $A_1$
is
$A_1$
is
![]() $E'$
-invariant and analytic, while
$E'$
-invariant and analytic, while
![]() $A_2$
is coanalytic, invariant analytic separation (Lemma 2.7) yields an
$A_2$
is coanalytic, invariant analytic separation (Lemma 2.7) yields an
![]() $E'$
-invariant Borel set B such that
$E'$
-invariant Borel set B such that
![]() $A_1 \subseteq B \subseteq A_2$
.
$A_1 \subseteq B \subseteq A_2$
.
Fix a Borel linear ordering, say
![]() $\preccurlyeq $
, on X (for instance, we may assume that
$\preccurlyeq $
, on X (for instance, we may assume that
![]() $X = \mathbb {R}$
[Reference Kechris8, Theorem 15.6] and use the standard ordering on
$X = \mathbb {R}$
[Reference Kechris8, Theorem 15.6] and use the standard ordering on
![]() $\mathbb {R}$
). If
$\mathbb {R}$
). If
![]() $x \in B^c$
, then
$x \in B^c$
, then
![]() $[x]_{E'}$
is finite. Thus there exists a
$[x]_{E'}$
is finite. Thus there exists a
![]() $\preccurlyeq $
-minimum element, say
$\preccurlyeq $
-minimum element, say
![]() $\mu (x) \in B^c$
, such that
$\mu (x) \in B^c$
, such that
![]() $x \,E'\, \mu (x)$
. For each
$x \,E'\, \mu (x)$
. For each
![]() $x \in B^c$
, there are only finitely many
$x \in B^c$
, there are only finitely many
![]() $y \in X$
such that
$y \in X$
such that
![]() $x \,E'\, y$
, and so the map
$x \,E'\, y$
, and so the map
![]() $\mu : B^c \to B^c$
is Borel by the Luzin–Novikov theorem. Furthermore, for x,
$\mu : B^c \to B^c$
is Borel by the Luzin–Novikov theorem. Furthermore, for x,
![]() $y \in B^c$
, we have
$y \in B^c$
, we have
![]() $x \, E'\, y$
if and only if
$x \, E'\, y$
if and only if
![]() $\mu (x) = \mu (y)$
. On the other hand, if x,
$\mu (x) = \mu (y)$
. On the other hand, if x,
![]() $y \in B$
, then, since
$y \in B$
, then, since
![]() $B \subseteq A_2$
, we have
$B \subseteq A_2$
, we have
![]() $x \,E'\, y$
if and only if
$x \,E'\, y$
if and only if
![]() $f(x) = f(y)$
.
$f(x) = f(y)$
.
Without loss of generality, we may assume that
![]() $X \cap \mathbb {R} = \emptyset $
. Define
$X \cap \mathbb {R} = \emptyset $
. Define
![]() $g : X\to X \cup \mathbb {R}$
by
$g : X\to X \cup \mathbb {R}$
by

Since f and
![]() $\mu $
are Borel functions and B is a Borel set, g is a Borel function. Furthermore, the above discussion implies that g witnesses the smoothness of
$\mu $
are Borel functions and B is a Borel set, g is a Borel function. Furthermore, the above discussion implies that g witnesses the smoothness of
![]() $E'$
, as desired.
$E'$
, as desired.
7.2. Borel line graph relations for graphs with finite components
In this appendix we prove the following lemma, which was used in the proof of Theorem 3.6:
Lemma 7.2. Let L be a Borel graph with finite components. If L is a line graph, then L has a Borel line graph relation.
Statements such as Lemma 7.2 are considered routine in descriptive set theory. Indeed, Lemma 7.2 can be seen as a special case of certain general facts about Borel combinatorics on Borel graphs with finite components, for example, [Reference Pikhurko and Dabrowski16, Section 5.3] and [Reference Bernshteyn and Weilacher2, Section 2.2]. Nevertheless, in an effort to make this paper more accessible to non-experts, we present a complete proof here. In the following argument, it will be useful to keep in mind that if X is a standard Borel space and Y is a countable set, then a map
![]() $f \colon X \to Y$
is Borel if and only if
$f \colon X \to Y$
is Borel if and only if
![]() $f^{-1}(y)$
is a Borel set for each
$f^{-1}(y)$
is a Borel set for each
![]() $y \in Y$
.
$y \in Y$
.
Proof. Let L be a Borel graph with finite components such that L is a line graph. For each
![]() $x \in V(L)$
, let
$x \in V(L)$
, let
![]() $[x]$
denote the component of L containing x. Since the components of L are finite, the Luzin–Novikov theorem implies that the relation
$[x]$
denote the component of L containing x. Since the components of L are finite, the Luzin–Novikov theorem implies that the relation ![]() is Borel (see Examples 2.3 and 2.5). Fix a Borel linear ordering, say
is Borel (see Examples 2.3 and 2.5). Fix a Borel linear ordering, say
![]() $\preccurlyeq $
, on
$\preccurlyeq $
, on
![]() $V(L)$
(for instance, we may assume that
$V(L)$
(for instance, we may assume that
![]() $V(L) = \mathbb {R}$
[Reference Kechris8, Theorem 15.6] and use the standard ordering on
$V(L) = \mathbb {R}$
[Reference Kechris8, Theorem 15.6] and use the standard ordering on
![]() $\mathbb {R}$
). Define a function
$\mathbb {R}$
). Define a function
![]() ${r : V(L) \to {\mathbb {N}}}$
by
${r : V(L) \to {\mathbb {N}}}$
by
 $$ \begin{align*} r(x) = k &\iff x \text{ is the } k\text{th element of } V([x]) \text{ under } \preccurlyeq \\ & \iff \exists\, x_1, \dots, x_{k-1} \in V([x])\, \big((x_1 \prec x_2 \prec \cdots \prec x_{k-1} \prec x) \text{ and}\\ &\hspace{2in}\forall\, y \in V([x]){\setminus}\{x_1, \dots, x_{k-1}\}\, (x \preccurlyeq y)\big). \end{align*} $$
$$ \begin{align*} r(x) = k &\iff x \text{ is the } k\text{th element of } V([x]) \text{ under } \preccurlyeq \\ & \iff \exists\, x_1, \dots, x_{k-1} \in V([x])\, \big((x_1 \prec x_2 \prec \cdots \prec x_{k-1} \prec x) \text{ and}\\ &\hspace{2in}\forall\, y \in V([x]){\setminus}\{x_1, \dots, x_{k-1}\}\, (x \preccurlyeq y)\big). \end{align*} $$
As
![]() $[x]$
is finite, all the quantifiers in the above definition range over finite sets, so the function r is Borel by the Luzin–Novikov theorem. The map
$[x]$
is finite, all the quantifiers in the above definition range over finite sets, so the function r is Borel by the Luzin–Novikov theorem. The map ![]() is also Borel, since we can write
is also Borel, since we can write
Next we define, for each positive integer k, a partial mapping
![]() $n_k \colon V(L) \dashrightarrow V(L)$
as follows:
$n_k \colon V(L) \dashrightarrow V(L)$
as follows:
The function
![]() $n_k$
is again Borel. Note that for each
$n_k$
is again Borel. Note that for each
![]() $x \in V(L)$
,
$x \in V(L)$
,
Let
![]() $\mathcal {G}^{<\infty }$
be the (countable) set of all finite line graphs with vertex set a subset of
$\mathcal {G}^{<\infty }$
be the (countable) set of all finite line graphs with vertex set a subset of
![]() ${\mathbb {N}}$
. For every
${\mathbb {N}}$
. For every
![]() $\Gamma \in \mathcal {G}^{<\infty }$
, fix an arbitrary line graph relation
$\Gamma \in \mathcal {G}^{<\infty }$
, fix an arbitrary line graph relation
![]() $\sim _\Gamma $
on
$\sim _\Gamma $
on
![]() $\Gamma $
. Given
$\Gamma $
. Given
![]() $x \in V(L)$
, define
$x \in V(L)$
, define
![]() $\Gamma _x \in \mathcal {G}^{<\infty }$
by
$\Gamma _x \in \mathcal {G}^{<\infty }$
by
Then r establishes an isomorphism
![]() $[x] \cong \Gamma _x$
, and if
$[x] \cong \Gamma _x$
, and if
![]() $y \equiv x$
, then
$y \equiv x$
, then
![]() $\Gamma _x = \Gamma _y$
. Since the set
$\Gamma _x = \Gamma _y$
. Since the set
![]() $E(L)$
and the functions s and
$E(L)$
and the functions s and
![]() $n_k$
for all k are Borel, the map
$n_k$
for all k are Borel, the map
![]() $V(L) \to \mathcal {G}^{<\infty } \colon x \mapsto \Gamma _x$
is Borel as well. (To clarify, this means that for each graph
$V(L) \to \mathcal {G}^{<\infty } \colon x \mapsto \Gamma _x$
is Borel as well. (To clarify, this means that for each graph
![]() $\Gamma \in \mathcal {G}^{<\infty }$
, the set of all
$\Gamma \in \mathcal {G}^{<\infty }$
, the set of all
![]() $x \in V(L)$
with
$x \in V(L)$
with
![]() $\Gamma _x = \Gamma $
is Borel.)
$\Gamma _x = \Gamma $
is Borel.)
Finally, we define a relation
![]() $\sim $
on
$\sim $
on
![]() $E(L)$
as follows: if
$E(L)$
as follows: if
![]() $e = xy$
and
$e = xy$
and
![]() $f = uv$
, let
$f = uv$
, let
In other words,
![]() $\sim $
is obtained by “copying”
$\sim $
is obtained by “copying”
![]() $\sim _{\Gamma _x}$
from
$\sim _{\Gamma _x}$
from
![]() $\Gamma _x$
onto
$\Gamma _x$
onto
![]() $[x]$
for each
$[x]$
for each
![]() $x \in V(L)$
in the obvious way. It is now clear that
$x \in V(L)$
in the obvious way. It is now clear that
![]() $\sim $
is a desired Borel line graph relation on L.
$\sim $
is a desired Borel line graph relation on L.
Acknowledgements
We thank the anonymous referees for their careful reading of this manuscript and helpful suggestions.
Funding
This research is partially supported by the NSF grant DMS-2045412 and the NSF CAREER grant DMS-2239187.