Hostname: page-component-cc8bf7c57-fxdwj Total loading time: 0 Render date: 2024-12-11T22:12:54.640Z Has data issue: false hasContentIssue false
  • English
  • Français

Blunt and topless end extensions of models of set theory

Published online by Cambridge University Press:  12 March 2014

Matt Kaufmann
Matt Kaufmann*
Affiliation:
Purdue University, West Lafayette, Indiana 47907
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 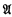be a well-founded model of ZFC whose class of ordinals has uncountable cofinality, such that 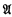has a Σn end extension for each n ∈ ω. It is shown in Theorem 1.1 that there is such a model which has no elementary end extension. In the process some interesting facts about topless end extensions (those with no least new ordinal) are uncovered, for example Theorem 2.1: If 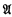is a well-founded model of ZFC, such that 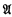has uncountable cofinality and 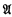has a topless Σ3 end extension, then 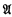has a topless elementary end extension and also a well-founded elementary end extension, and contains ordinals which are (in 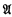) highly hyperinaccessible. In §3 related results are proved for κ-like models (κ any regular cardinal) which need not be well founded. As an application a soft proof is given of a theorem of Schmerl on the model-theoretic relation κ → λ. (The author has been informed that Silver had earlier, independently, found a similar unpublished proof of that theorem.) Also, a simpler proof is given of (a generalization of) a characterization by Keisler and Silver of the class of well-founded models which have a Σn end extension for each n ∈ ω. The case κ = ω1 is investigated more deeply in §4, where the problem solved by Theorem 1.1 is considered for non-well-founded models. In Theorems 4.1 and 4.4, ω1-like models of ZFC are constructed which have a Σn end extension for all n ∈ ω but have no elementary end extension. ω1-like models of ZFC which have no Σ3 end extension are produced in Theorem 4.2. The proof uses a notion of satisfaction class, which is also applied in the proof of Theorem 4.6: No model of ZFC has a definable end extension which satisfies ZFC. Finally, Theorem 5.1 generalizes results of Keisler and Morley, and Hutchinson, by asserting that every model of ZFC of countable cofinality has a topless elementary end extension. This contrasts with the rest of the paper, which shows that for well-founded models of uncountable cofinality and for κ-like models with κ regular, topless end extensions are much rarer than blunt end extensions.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 48 , Issue 4 , December 1983 , pp. 1053 - 1073
Copyright
Copyright © Association for Symbolic Logic 1983

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[B]Barwise, J., Admissible sets and structures, Springer-Verlag, Berlin, 1975.CrossRefGoogle Scholar
[F]Felgner, U., Comparisons of the axioms of local and universal choice, Fundamenta Mathematicae, vol. 71 (1971), pp. 43–62.CrossRefGoogle Scholar
[H]Hutchinson, J. E., Elementary extensions of countable models of set theory, this Journal, vol. 41 (1976), pp. 139–145.Google Scholar
[Ka]Kaufmann, M., Blunt and topless end extensions, Abstracts of the American Mathemetical Society, vol. 3 (1982), pp. 183–184.Google Scholar
[K]Keisler, H. J., Models with tree structures, Proceedings of the Tarski Symposium, Proceedings of Symposia in Pure Mathematics, American Mathematical Society, Providence, R.I., 1974, pp. 331–348.Google Scholar
[KM]Keisler, H. J. and Morley, M., Elementary extensions of models of set theory, Israel Journal of Mathematics, vol. 5 (1968), pp. 49–65.CrossRefGoogle Scholar
[KS]Keisler, H. J. and Silver, J., End extensions of models of set theory, Axiomatic Set Theory (Part 1), Proceedings of Symposia in Pure Mathematics, vol. 13, American Mathematical Society, Providence, R.I., 1970, pp. 177–187.Google Scholar
[MaSp]MacDowell, R. and Specker, E., Modelle der Arithmetik, Infinitistic Methods, Proceedings of Symposium in Foundations of Mathematics (Warsaw, 1959), Pergamon Press, New York, 1961, pp. 257–263.Google Scholar
[MnV]Montague, R. and Vaught, R. L., Natural models of set theories, Fundamenta Mathematicae, vol. 47 (1959), pp. 219–242.CrossRefGoogle Scholar
[Ms]Mostowski, A., An undecidable arithmetical statement, Fundamenta Mathematicae, vol. 36 (1949), pp. 143–164.CrossRefGoogle Scholar
[R]Ratajczyk, Z., On axiomatization of ZFKMand ZFKM (to appear).Google Scholar
[Sc1]Schmerl, J., An elementary sentence which has ordered models, this Journal, vol. 37 (1972), pp. 521–530.Google Scholar
[Sc2]Schmerl, J., On κ-like structures which embed closed unbounded sets, Annals of Mathematical Logic, vol. 10 (1976), pp. 289–314.CrossRefGoogle Scholar
[ScSh]Schmerl, J. and Shelah, S., On power-like models for hyperinaccessible cardinals, this Journal, vol. 37 (1972), pp. 531–537.Google Scholar
[Sh]Shelah, S., Models with second-order properties. II. Trees with no undefined branches, Annals of Mathematical Logic, vol. 14(1978), pp. 73–87.CrossRefGoogle Scholar
[Sm]Smoryński, C., The incompleteness theorems, Handbook of Mathematical Logic (Barwise, J., Editor), North-Holland, Amsterdam, 1978, pp. 821–865.Google Scholar