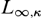Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-27T10:06:04.042Z Has data issue: false hasContentIssue false
  • English
  • Français

AN ABSTRACT ELEMENTARY CLASS NONAXIOMATIZABLE IN ${L_{\infty ,\kappa }}$

Published online by Cambridge University Press:  03 April 2019

SIMON HENRY
SIMON HENRY*
Affiliation:
DEPARTMENT OF MATHEMATICS AND STATISTICS MASARYK UNIVERSITY BUILDING 08 KOTLÁŘSKÁ 2 611 37 BRNO, CZECH REPUBLIC E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that for any uncountable cardinal λ, the category of sets of cardinality at least λ and monomorphisms between them cannot appear as the category of points of a topos, in particular is not the category of models of a 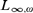${L_{\infty ,\omega }}$-theory. More generally we show that for any regular cardinal 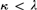$\kappa < \lambda$ it is neither the category of κ-points of a κ-topos, in particular, nor the category of models of a 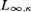${L_{\infty ,\kappa }}$-theory.

The proof relies on the construction of a categorified version of the Scott topology, which constitute a left adjoint to the functor sending any topos to its category of points and the computation of this left adjoint evaluated on the category of sets of cardinality at least λ and monomorphisms between them. The same techniques also apply to a few other categories. At least to the category of vector spaces of with bounded below dimension and the category of algebraic closed fields of fixed characteristic with bounded below transcendence degree.

Keywords

18C3518C1003G3003C48toposespoints of toposesScott topologyabstract elementary classes
Type
Articles
Information
The Journal of Symbolic Logic , Volume 84 , Issue 3 , September 2019 , pp. 1240 - 1251
Copyright
Copyright © The Association for Symbolic Logic 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Adámek, J. and Rosický, J., Locally Presentable and Accessible Categories, vol. 189, Cambridge University Press, Cambridge, 1994.Google Scholar
Beke, T. and Rosický, J., Abstract elementary classes and accessible categories. Annals of Pure and Applied Logic, vol. 163 (2012), no. 12, pp. 2008–2017.Google Scholar
Borceux, F., Handbook of Categorical Algebra 3: Sheaf Theory, vol. 3, Cambridge University Press, Cambridge, 1994.Google Scholar
Espíndola, C., Infinitary generalizations of Deligne’s completeness theorem, arXiv preprint, 2017, arXiv:1709.01967.Google Scholar
Johnstone, P. T., Sketches of an Elephant: A Topos Theory Compendium, Clarendon Press, Oxford, 2002.Google Scholar
MacLane, S. and Moerdijk, I., Sheaves in Geometry and Logic: A First Introduction to Topos Theory, Springer, New York, 1992.Google Scholar
Makkai, M. and Paré, R., Accessible Categories: The Foundations of Categorical Model Theory , Contemporary Mathematics, vol. 104, American Mathematical Society, Providence, RI, 1989.Google Scholar