Article contents
Witnessing functions in bounded arithmetic and search problems
Published online by Cambridge University Press: 12 March 2014
Abstract
We investigate the possibility to characterize (multi)functions that are  -definable with small i (i = 1, 2, 3) in fragments of bounded arithmetic T2 in terms of natural search problems defined over polynomial-time structures. We obtain the following results:
-definable with small i (i = 1, 2, 3) in fragments of bounded arithmetic T2 in terms of natural search problems defined over polynomial-time structures. We obtain the following results:
(1) A reformulation of known characterizations of (multi)functions that are 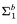 and
and 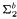 -definable in the theories
-definable in the theories 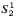 and
and 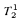 .
.
(2) New characterizations of (multi)functions that are 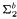 and
and 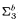 -definable in the theory
-definable in the theory 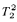 .
.
(3) A new non-conservation result: the theory 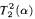 is not
is not 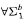 -conservative over the theory
-conservative over the theory 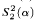 .
.
To prove that the theory 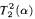 is not
is not 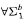 -conservative over the theory
-conservative over the theory 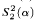 , we present two examples of a
, we present two examples of a 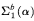 -principle separating the two theories:
-principle separating the two theories:
(a) the weak pigeonhole principle WPHP(a2, f, g) formalizing that no function f is a bijection between a2 and a with the inverse g,
(b) the iteration principle Iter(a, R, f) formalizing that no function f defined on a strict partial order ({0,…, a}, R) can have increasing iterates.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1998
References
REFERENCES
- 16
- Cited by


