Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Farah, Ilijas
and
Zapletal, Jindřich
2006.
Four and more.
Annals of Pure and Applied Logic,
Vol. 140,
Issue. 1-3,
p.
3.
Jackson, Steve
2010.
Handbook of Set Theory.
p.
1753.
Sargsyan, Grigor
2019.
An inner model theoretic proof of Becker’s theorem.
Archive for Mathematical Logic,
Vol. 58,
Issue. 7-8,
p.
999.
Crone, Logan
Fishman, Lior
and
Jackson, Stephen
2022.
Hausdorff dimension regularity properties and games.
Israel Journal of Mathematics,
Vol. 248,
Issue. 1,
p.
481.


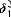 -supercompact. In particular, all the projective ordinals
-supercompact. In particular, all the projective ordinals 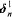 are
are 