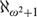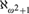Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Du, Jin
2019.
The strong tree property and the failure of SCH.
Archive for Mathematical Logic,
Vol. 58,
Issue. 7-8,
p.
867.
Poveda, Alejandro
2020.
The tree property at first and double successors of singular cardinals with an arbitrary gap.
Annals of Pure and Applied Logic,
Vol. 171,
Issue. 5,
p.
102778.
Unger, Spencer
2021.
Successive failures of approachability.
Israel Journal of Mathematics,
Vol. 242,
Issue. 2,
p.
663.
Honzik, Radek
Lambie-Hanson, Chris
and
Stejskalová, Šárka
2024.
Indestructibility of some compactness principles over models of PFA.
Annals of Pure and Applied Logic,
Vol. 175,
Issue. 1,
p.
103359.
Gilton, Thomas
and
Stejskalová, Šárka
2025.
Club stationary reflection and other combinatorial principles at ℵ+2.
Annals of Pure and Applied Logic,
Vol. 176,
Issue. 1,
p.
103489.