No CrossRef data available.
Published online by Cambridge University Press: 12 March 2014
Consistency properties and their model existence theorems have provided an important method of constructing models for fragments of L∞ω. In [E] Ellentuck extended this construction to Suslin logic. One of his extensions, the Borel consistency property, has its extra rule based not on the semantic interpretation of the extra symbols but rather on a theorem of Sierpinski about the classical operation 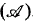 . In this paper we extend that consistency property to the game logic LG and use it to show how one can extend results about
. In this paper we extend that consistency property to the game logic LG and use it to show how one can extend results about 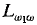 and its countable fragments to LG and certain of its countable fragments. The particular formation of LG which we use will allow in the game quantifier infinite alternation of countable conjunctions and disjunctions as well as infinite alternation of quantifiers. In this way LG can be viewed as an extension of Suslin logic.
and its countable fragments to LG and certain of its countable fragments. The particular formation of LG which we use will allow in the game quantifier infinite alternation of countable conjunctions and disjunctions as well as infinite alternation of quantifiers. In this way LG can be viewed as an extension of Suslin logic.
The research for this paper was done while the author was a visitor at Howard University with financial support from the Rutgers University Faculty Academic Study Program.