Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-25T05:52:08.003Z Has data issue: false hasContentIssue false
  • English
  • Français

Real functions on the family of all well-ordered subsets of a partially ordered set1

Published online by Cambridge University Press:  12 March 2014

Stevo Todorčević
Stevo Todorčević*
Affiliation:
Matematički Institut, Beograd, Jugoslavija
*
Current address: Department of Mathematics, University of Colorado, Boulder, Colorado 80309
Get access Rights & Permissions [Opens in a new window]

Extract

Definition 1 (Kurepa [3, p. 99]). Let E be a partially ordered set. Then σE denotes the set of all bounded well-ordered subsets of E. We consider σE as a partially ordered set with ordering 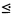defined as follows: s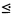t if and only if s is an initial segment of t.

Then σE is a tree, i.e., {s ∈ σ E∣ s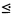t} is well-ordered for every t ∈ σE. The trees of the form αE were extensively studied by Kurepa in [3]–[10]. For example, in [4], he used σQ and σR to construct various sorts of Aronszajn trees. (Here Q and R denote the rationals and reals, respectively.) While considering monotone mapping between some kind of ordered sets, he came to the following two questions several times:

P.1. Does there exist a strictly increasing rational function on σQ? (See [4, Problème 2], [5, p. 1033], [6, p. 841], [7, Problem 23.3.3].)

P.2. Let T be a tree in which every chain is countable and every level has cardinality <2ℵ0. Does there exist a strictly increasing real function on T? (See [6, p. 246] and [7].)

It is known today that Problem 2 is independent of the usual axioms of set theory (see [1]). Concerning Problem 1 we have the following.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 48 , Issue 1 , March 1983 , pp. 91 - 96
Copyright
Copyright © Association for Symbolic Logic 1983

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

This paper was written while we were visiting the Hebrew University of Jerusalem in the first part of 1980. We wish to express here our gratitude to the Department of Mathematics for its hospitality.

References

REFERENCES

[1]Baumgartner, J., Malitz, J. and Reinhardt, W., Embedding trees in the rationals, Proceedings of the National Academy of Sciences of the U.S.A., vol. 67 (1970), pp. 1748–1753.CrossRefGoogle ScholarPubMed
[2]Galvin, F., On a partition theorem of Baumgartner and Hajnal, Colloquia Mathematica Societatis Janos Bolyai, vol. 10; Infinite and finite sets, Keszthely, Hungary, 1973, North-Holland, Amsterdam, 1975, pp. 711–729.Google Scholar
[3]Kurepa, D., Ensembles ordonnés et ramifiés, Thèse, Paris; Publications Mathématiques de l'Université de Belgrade, vol. 4 (1935), pp. 1–138.Google Scholar
[4]Kurepa, D., Ensembles linéaires et une classe de tableaux ramifiés (Tableaux ramifiés de M. Aronszajn), Publications Mathématiques de l'Université de Belgrade, vol. 6 (1937), pp. 129–160.Google Scholar
[5]Kurepa, D., Transformations monotones des ensembles partiellement ordonnés, Comptes Rendus Hebdomadaires des Séances de l'Académic des Sciences (Paris), vol. 205 (1937), pp. 1033–1035.Google Scholar
[6]Kurepa, D., Transformations monotones des ensembles partiellement ordonnés, Revista da Ciencias (Lima), vol. 434 (42)(1940), pp. 827–846; vol. 437 (43)(1941), pp. 834–500.Google Scholar
[7]Kurepa, D., Teorija Skupova, Skolska knjiga, Zagreb, 1951.Google Scholar
[8]Kurepa, D., Fonctions croissantes dans la famille des ensembles bien ordonnés linéaires, Bulletin Scientifique Yougoslave, vol. 2 (1) (1954), p. 9.Google Scholar
[9]Kurepa, D., Sur les fonctions réelles dans la famille des ensembles bien ordonnés de nombres rationels, Bulletin International de l'Académic Yougoslave des Sciences et des Beaux-Arts, vol. 4 (1954), pp. 35–12.Google Scholar
[10]Kurepa, D., Monotone mappings between some kinds of ordered sets, Glasnik Matematicko-Fizički i Astronomski, vol. 19 (3–4)(1964), pp. 175–186.Google Scholar
[11]Todorčević, S., Real functions on the family of all well ordered subsets of a set, Abstracts of Papers Presented to the American Mathematical Society, vol. 1 (5) (1980), p. A–494.Google Scholar
[12]Todorčević, S., A partition relation for partially ordered sets, Abstracts of Papers Presented to the American Mathematical Society, vol. 2 (3) (1981), p. A–362.Google Scholar