Published online by Cambridge University Press: 12 March 2014
For a ring with unit R, which need not be associative, denote the group of upper unitriangular 3 × 3 matrices over R by UT3(R). Let e1 = (1,0,0), e2 = (0,1,0), where (α, β, γ) denotes the matrix
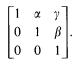
Denote the expanded group (UT3(R), e1, e2) by 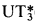 (R). A. 1. Mal′cev [M] gave an algebraic characterization of the expanded groups of the form
(R). A. 1. Mal′cev [M] gave an algebraic characterization of the expanded groups of the form 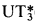 (R) as follows. Let h1, h2 be elements of a group H; then (H, h1, h2) is isomorphic to
(R) as follows. Let h1, h2 be elements of a group H; then (H, h1, h2) is isomorphic to 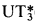 (R), for some R, if and only if
(R), for some R, if and only if
(i) H is 2-step nilpotent;
(ii) CH(hi) are abelian, i = 1,2;
(iii) CH(h1) ∩ CH(h2) = Z(H);
(iv) [CH(h1),h2] = [h1, CH(h2)] = Z(H);
(v) Z(H) is a direct summand in both CH(hi).
(In [M] condition (v) is a bit stronger; the version above is presented in [B2].)
A pair (h1, h2) of elements of a group H is said to be a base if (H, h1, h2) satisfies the conditions (i)–(iv). A. I. Mal′cev [M] found a uniform way of first order interpreting a ring Ring(H, h1, h2) in any group with a base (H, h1, h2); in particular, Ring(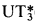 (R)) ≃ R.
(R)) ≃ R.