Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Soskova, Mariya I.
2013.
The Nature of Computation. Logic, Algorithms, Applications.
Vol. 7921,
Issue. ,
p.
371.
Ganchev, Hristo
and
Soskova, Mariya
2014.
Definability via Kalimullin pairs in the structure of the enumeration degrees.
Transactions of the American Mathematical Society,
Vol. 367,
Issue. 7,
p.
4873.
2016.
Algebraic Computability and Enumeration Models.
p.
155.


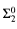 enumeration degrees and the high/low hierarchy
enumeration degrees and the high/low hierarchy