Published online by Cambridge University Press: 12 March 2014
We consider any set of Gentzen-type rules in a formal system of the following sort. The terms of the system are propositions, generally to be thought of as the propositions of some underlying theory. The elementary statements are of the form

where 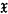 and
and 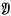 are finite sequences of propositions and (1) expresses a relation, called entailment, between such sequences. These sequences will be called prosequences; they may be void, or consist of a single proposition; and they may contain repetitions of the same proposition. The members of a prosequence will be called its constituents. Two prosequences which are permutations of one another will be regarded as the same. Prosequences will be designated by German letters, single propositions by Latin ones.
are finite sequences of propositions and (1) expresses a relation, called entailment, between such sequences. These sequences will be called prosequences; they may be void, or consist of a single proposition; and they may contain repetitions of the same proposition. The members of a prosequence will be called its constituents. Two prosequences which are permutations of one another will be regarded as the same. Prosequences will be designated by German letters, single propositions by Latin ones.
The rules of the system are to be of the following form:
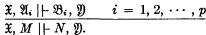
This notation is to be understood as indicating p premises and a conclusion, each of the form (1). The constituents of 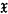 and
and 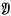 occur in all premises and conclusion; they are called the parametric constituents, or simply the parameters, of the inference.
occur in all premises and conclusion; they are called the parametric constituents, or simply the parameters, of the inference.
Presented (by title) to a joint meeting of the Association for Symbolic Logic and the American Mathematical Society, December 30, 1948.
2 A theory of formal deducibility. Notre Dame Mathematical Lectures, No. 6, 1950 Google Scholar. These lectures will be referred to as TFD. The rule Er is not to be included. Except for some changes in notation the rules are the same as in Gentzen's thesis cited below in footnote 3.
3 See Gentzen, G., Untersuchungen über das logische Schliessen, Mathematische Zeitschrift, vol. 39 (1934), pp. 176–210, 405–431 CrossRefGoogle Scholar. Cf. also Ketonen, O., Untersuchungen zum Pradikäten-kalkül, Annales Academiae Scientiarum Fennicae, ser. A, I. Mathematica-physica, No. 23 (1944)Google Scholar. Much of what follows is found in these papers of Gentzen and Ketonen. Gentzen's paper should be consulted for the connection of his theorem with an earlier theorem of Herbrand. Ketonen's paper also contains a proof of the equivalence of the classical algebra with the truth table evaluation which is vastly superior to anything previously given; it should replace the references in TFD IV, Theorem 12.
4 The left-hand argument is in Gentzen (l.c.).
5 I.e. Beweisfäden, in the sense used by the Hilbert school—i.e., any series of statements formed by going upwards from the final result and making an arbitrary choice at each inference with more than one premise.
6 By the same method it can be shown that the case pi of a prime statement can be restricted by the condition that the common constituent A be elementary.