The order indiscernibles of divisible ordered abelian groups

Extract

There has been much work in developing the interconnections between model theory and algebra. Here we look at a particular example, the divisible ordered abelian groups, and show how the indiscernibles are related to the algebraic structure. Now a divisible ordered abelian group is a model of Th (Q, +, 0, <) and so is linearly ordered by <. Thus the theory is unstable and has a large number of models. It is therefore unrealistic to expect that a simple condition will completely determine a model. Instead we would just like to obtain nice algebraic invariants.

Definition. A subset C of a divisible ordered abelian group 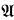is a set of (order) indiscernibles iff for every sequence of integers n₁,…,n_k and for every c₁ < … < c_k and d₁ < … < d_k in C

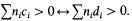
Note that this simplified form of indiscernibility is an immediate consequence of quantifier elimination for the theory. The above definition could be formulated in the language of +, 0, < but we have used subtraction as a matter of convenience. Similarly we may also use rational coefficients. Also note that a set of order indiscernibles is usually defined with respect to some external order. But in this case there are only two possibilities: the ordering inherited from 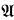or its reverse. So we will always assume that a set of order indiscernibles has the ordering inherited from 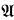. We may sometimes refer to a set of indiscernibles as a sequence of indiscernibles if we want to explicitly mention the ordering associated with the set.