Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-25T01:32:28.308Z Has data issue: false hasContentIssue false
  • English
  • Français

Open questions in the theory of spaces of orderings

Published online by Cambridge University Press:  12 March 2014

Murray A. Marshall
Murray A. Marshall*
Affiliation:
Department of Mathematics & Statistics, University of Saskatchewan, Saskatoon, SK., CanadaS7N 0W0, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

Spaces of orderings provide an abstract framework in which to study spaces of orderings of formally real fields. Spaces of orderings of finite chain length are well understood [9, 11]. The Isotropy Theorem [11] and the extension of the Isotropy Theorem given in [13] are the main tools for reducing questions to the finite case, and these are quite effective. At the same time, there are many questions which do not appear to reduce in this way. In this paper we consider four such questions, for a space of orderings (X, G).

1. Is it true that every positive primitive formula P(a) with parameters a in G which holds in every finite subspace of (X, G) necessarily holds in (X, G)?

2. If f: X → ℤ is continuous and Σx∈Vf(x) ≡ 0 mod ∣V∣ holds for all fans V in X with ∣V∣ ≤ 2n, does there exist a form ϕ with entries in G such that 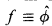mod Cont(X, 2nℤ)?

3. Is it true that Cont(X, 2nℤ) ∩ Witt(X, G) = In(X, G), where I(X, G) denotes the fundamental ideal?

4. Is the separating depth of a constructible set C in X necessarily bounded by the stability index of (X, G)?

The unexplained terminology and notation is explained later in the main body of the paper. In a certain sense Question 1 is the main question. At the same time, Questions 2, 3 and 4 are of considerable interest, both from the point of view of quadratic form theory and from the point of view of real algebraic geometry.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 67 , Issue 1 , March 2002 , pp. 341 - 352
Copyright
Copyright © Association for Symbolic Logic 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Andradas, C., Bröcker, L., and Ruiz, J., Constructible sets in real geometry, Ergebnisse der Mathematik und ihrer Grenzgebiete, no. 33, Springer, 1996.CrossRefGoogle Scholar
[2]Bonnard, I., Un critère pour reconnaître lesfonctions algébriquement constructibles, preprint.Google Scholar
[3]Bonnard, I., Fonctions algébriquement constructibles el formes quadmtiques, PhD thesis, Angers, 2000.CrossRefGoogle Scholar
[4]Bröcker, L., Spaces of orderings and semi-algebraic sets, Quadratic and Hermitian forms, Canadian Mathematical Society Conference Proceedings, 1984, pp. 231–248.Google Scholar
[5]Craven, T., Characterizing reduced Witt rings of fields, Journal of Algebra, (1978), pp. 68–77.Google Scholar
[6]Dickmann, M. and Miraglia, F., Lam's problem, preprint.Google Scholar
[7]Dickmann, M., Pfister indices, preprint.Google Scholar
[8]Dickmann, M., Special groups: Boolean-theoretic methods in the theory of quadratic forms, Memoirs of the American Mathematical Society, (2000). no. 689.Google Scholar
[9]Marshall, M., Classification of finite spaces of orderings, Canadian Journal of Mathematics, vol. 31 (1979), pp. 320–330.CrossRefGoogle Scholar
[10]Marshall, M., Quotients and inverse limits of spaces of orderings, Canadian Journal of Mathematics, vol.31 (1979), pp. 604–616.CrossRefGoogle Scholar
[11]Marshall, M., Spaces of orderings IV, Canadian Journal of Mathematics, vol. 32 (1980), pp. 603–627.CrossRefGoogle Scholar
[12]Marshall, M., The Witt ring of a space of orderings, Transactions of the American Mathematical Society, (1980), pp. 505–521.Google Scholar
[13]Marshall, M., Spaces of orderings: systems of quadratic forms, local structure and saturation, Communications in Algebra, vol. 12 (1984), pp. 723–743.CrossRefGoogle Scholar
[14]Marshall, M., On Bröcker's t-invariant and separating families for constructible sets, Aequationes Mathematicae vol. 48 (1994), pp. 306–316.CrossRefGoogle Scholar
[15]Marshall, M., Spaces of orderings and abstract real spectra, Lecture Notes in Mathematics, no. 1636, Springer, 1996.CrossRefGoogle Scholar