Article contents
One theorem of Zil′ber's on strongly minimal sets
Published online by Cambridge University Press: 12 March 2014
Abstract
Suppose D ⊂ M is a strongly minimal set definable in M with parameters from C. We say D is locally modular if for all X, Y ⊂ D, with X = acl(X ∪ C)∩D, Y = acl(Y ∪ C) ∩ D and X ∩ Y ≠ ∅,
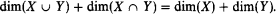
We prove the following theorems.
Theorem 1. Suppose M is stable and D ⊂ M is strongly minimal. If D is not locally modular then inMeqthere is a definable pseudoplane.
(For a discussion of Meq see [M, §A].) This is the main part of Theorem 1 of [Z2] and the trichotomy theorem of [Z3].
Theorem 2. Suppose M is stable and D, D′ ⊂ M are strongly minimal and nonorthogonal. Then D is locally modular if and only if D′ is locally modular.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1985
References
REFERENCES
- 5
- Cited by


