Published online by Cambridge University Press: 12 March 2014
Mr. L. J. Cohen's interesting example of a logical truth of indirect discourse appears to be capable of a simple formalisation and proof in a variant of first order predicate calculus. His example has the form:
If A says that anything which B says is false, and B says that something which A says is true, then something which A says is false and something which B says is true.
Let ‘A says x’ be formalised by ‘A(x)’ and let assertions of truth and falsehood be formalised as in the following table.

We treat both variables x and predicates A (x) as sentences and add to the familiar axioms and inference rules of predicate logic a rule permitting the inference of A(p) from (x)A(x), where p is a closed sentence.
We have to prove that from
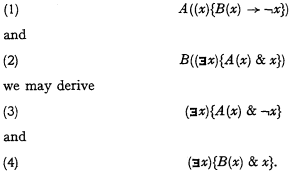
1 This Journal, Vol. 22, no. 3 (1957), pp. 225–232.