Article contents
On o-minimal expansions of Archimedean ordered groups
Published online by Cambridge University Press: 12 March 2014
Abstract
We study o-minimal expansions of Archimedean totally ordered groups. We first prove that any such expansion must be elementarily embeddable via a unique (provided some nonzero element is 0-definable) elementary embedding into a unique o-minimal expansion of the additive ordered group of real numbers 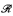 . We then show that a definable function in an o-minimal expansion of
. We then show that a definable function in an o-minimal expansion of 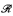 enjoys good differentiability properties and use this to prove that an Archimedean real closed field is definable in any nonsemilinear expansion of
enjoys good differentiability properties and use this to prove that an Archimedean real closed field is definable in any nonsemilinear expansion of 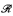 . Combining these results, we obtain several restrictions on possible o-minimal expansions of arbitrary Archimedean ordered groups and in particular of the rational ordered group.
. Combining these results, we obtain several restrictions on possible o-minimal expansions of arbitrary Archimedean ordered groups and in particular of the rational ordered group.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1995
References
REFERENCES
- 9
- Cited by


