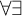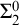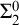1 Introduction
Enumeration reducibility is a natural counterpart to its more famous cousin, Turing reducibility, and arises naturally as a notion of relative computability especially in computable model theory as well as, in slightly modified form, Ziegler reducibility in group theory.
This paper is devoted to the study of enumeration reducibility in terms of a degree structure, more specifically, the degree structure of the enumeration degrees of the
![]() ${\Sigma ^0_2}$
-sets, which can be defined also as those enumeration degrees below the degree
${\Sigma ^0_2}$
-sets, which can be defined also as those enumeration degrees below the degree
![]() ${\mathbf 0}_e'$
, i.e., the enumeration degree of the complement
${\mathbf 0}_e'$
, i.e., the enumeration degree of the complement
![]() $\overline {K}$
of the halting problem
$\overline {K}$
of the halting problem
![]() $K = \{e \mid \varphi _e(e)\!\downarrow \,\}$
. (By this double characterization, the
$K = \{e \mid \varphi _e(e)\!\downarrow \,\}$
. (By this double characterization, the
![]() ${\Sigma ^0_2}$
-enumeration degrees can be viewed as the counterpart of both the c.e. Turing degrees and the Turing degrees
${\Sigma ^0_2}$
-enumeration degrees can be viewed as the counterpart of both the c.e. Turing degrees and the Turing degrees
![]() $\le {\mathbf 0}'$
, i.e., the
$\le {\mathbf 0}'$
, i.e., the
![]() $\Delta ^0_2$
-Turing degrees.)
$\Delta ^0_2$
-Turing degrees.)
One of the common questions about a degree structure viewed as a partial order is that of the complexity of its first-order theory as well as the decidability of fragments thereof. For most degree structures commonly being considered, the theory turns out to be as complicated as possible (i.e., equivalent to first-order or second-order arithmetic), while the
![]() $\exists $
-and often even the
$\exists $
-and often even the
![]() $\forall \exists $
-fragment is decidable and the
$\forall \exists $
-fragment is decidable and the
![]() $\exists \forall \exists $
-fragment is not.
$\exists \forall \exists $
-fragment is not.
For the
![]() ${\Sigma ^0_2}$
-enumeration degrees, the first of these questions has been completely settled: The full first-order theory was shown to be undecidable by Slaman and Woodin [Reference Slaman and Woodin13], and equivalent to full first-order arithmetic by Ganchev and Soskova [Reference Ganchev and Soskova3].
${\Sigma ^0_2}$
-enumeration degrees, the first of these questions has been completely settled: The full first-order theory was shown to be undecidable by Slaman and Woodin [Reference Slaman and Woodin13], and equivalent to full first-order arithmetic by Ganchev and Soskova [Reference Ganchev and Soskova3].
As for the second question, the
![]() $\exists $
-fragment is easily seen to be decidable, whereas Kent [Reference Kent6] showed the
$\exists $
-fragment is easily seen to be decidable, whereas Kent [Reference Kent6] showed the
![]() $\exists \forall \exists $
-fragment to be undecidable. On the other hand, the decidability of the
$\exists \forall \exists $
-fragment to be undecidable. On the other hand, the decidability of the
![]() $\forall \exists $
-fragment remains open.
$\forall \exists $
-fragment remains open.
The decidability of the
![]() $\forall \exists $
-fragment can be rephrased algebraically as (uniformly effectively) deciding the following.
$\forall \exists $
-fragment can be rephrased algebraically as (uniformly effectively) deciding the following.
Question 1.1. For any given finite partial orders
![]() ${\mathcal P}$
and
${\mathcal P}$
and
![]() ${\mathcal Q}_i \supseteq {\mathcal P}$
(for
${\mathcal Q}_i \supseteq {\mathcal P}$
(for
![]() $i \le n$
), can any embedding of
$i \le n$
), can any embedding of
![]() ${\mathcal P}$
into the
${\mathcal P}$
into the
![]() ${\Sigma ^0_2}$
-enumeration degrees be extended to an embedding of
${\Sigma ^0_2}$
-enumeration degrees be extended to an embedding of
![]() ${\mathcal Q}_i$
for some
${\mathcal Q}_i$
for some
![]() $i \le n$
(where i may depend on the particular embedding of
$i \le n$
(where i may depend on the particular embedding of
![]() ${\mathcal P}$
)?
${\mathcal P}$
)?
Two major subproblems of Question 1.1 have been shown to be decidable:
-
• Lempp, Slaman, and Sorbi [Reference Lempp, Slaman and Sorbi9] showed that the above question is decidable for
 $n=0$
, i.e., given any finite partial orders
$n=0$
, i.e., given any finite partial orders
 ${\mathcal P} \subseteq {\mathcal Q}$
, it is decidable whether any embedding of
${\mathcal P} \subseteq {\mathcal Q}$
, it is decidable whether any embedding of
 ${\mathcal P}$
into the
${\mathcal P}$
into the
 ${\Sigma ^0_2}$
-enumeration degrees can be extended to an embedding of
${\Sigma ^0_2}$
-enumeration degrees can be extended to an embedding of
 ${\mathcal Q}$
.
${\mathcal Q}$
. -
• Lempp and Sorbi [Reference Lempp and Sorbi10] showed that all finite lattices can be embedded, even preserving 0 and 1. (The lattice embeddings question can be seen as a disjunction of extending embeddings to certain one-point extensions
 ${\mathcal Q}_i$
of a finite lattice
${\mathcal Q}_i$
of a finite lattice
 ${\mathcal P}$
viewed as a partial order.)
${\mathcal P}$
viewed as a partial order.)
The
![]() ${\Sigma ^0_2}$
-enumeration degrees are often compared to the c.e. Turing degrees, where the situation is somewhat similar but also quite different in other respects: The full first-order theory is as complicated as first-order arithmetic by Slaman and Woodin (unpublished; see [Reference Nies, Shore and Slaman11]); the
${\Sigma ^0_2}$
-enumeration degrees are often compared to the c.e. Turing degrees, where the situation is somewhat similar but also quite different in other respects: The full first-order theory is as complicated as first-order arithmetic by Slaman and Woodin (unpublished; see [Reference Nies, Shore and Slaman11]); the
![]() $\exists $
-fragment is easily seen to be decidable, whereas Lempp, Nies, and Slaman [Reference Lempp, Nies and Slaman8] showed the
$\exists $
-fragment is easily seen to be decidable, whereas Lempp, Nies, and Slaman [Reference Lempp, Nies and Slaman8] showed the
![]() $\exists \forall \exists $
-fragment to be undecidable; the lattice embeddings problem for the c.e. Turing degrees remains one of the main open problems dating back to the 1960s (see [Reference Lempp, Lerman and Reed Solomon7] for the most recent update), and thus the decidability of the
$\exists \forall \exists $
-fragment to be undecidable; the lattice embeddings problem for the c.e. Turing degrees remains one of the main open problems dating back to the 1960s (see [Reference Lempp, Lerman and Reed Solomon7] for the most recent update), and thus the decidability of the
![]() $\forall \exists $
-theory of the c.e. Turing degrees remains wide open as well.
$\forall \exists $
-theory of the c.e. Turing degrees remains wide open as well.
The main algebraic difference between the c.e. Turing degrees and the
![]() ${\Sigma ^0_2}$
-enumeration degrees was discovered by Ahmad in her Ph.D. thesis [Reference Ahmad1] (see [Reference Ahmad and Lachlan2, Corollary 3.2]): There are incomparable
${\Sigma ^0_2}$
-enumeration degrees was discovered by Ahmad in her Ph.D. thesis [Reference Ahmad1] (see [Reference Ahmad and Lachlan2, Corollary 3.2]): There are incomparable
![]() ${\Sigma ^0_2}$
-enumeration degrees
${\Sigma ^0_2}$
-enumeration degrees
![]() ${\mathbf a}, {\mathbf b}$
(called an “Ahmad pair”) such that any degree
${\mathbf a}, {\mathbf b}$
(called an “Ahmad pair”) such that any degree
![]() ${\mathbf x} < {\mathbf a}$
is also
${\mathbf x} < {\mathbf a}$
is also
![]() $< {\mathbf b}$
. (This makes
$< {\mathbf b}$
. (This makes
![]() ${\mathbf a}$
“non-splitting” (i.e., join-irreducible) and thus cannot happen in the c.e. Turing degrees by the Sacks Splitting Theorem [Reference Sacks12].) More interestingly, even Ahmad also showed (see [Reference Ahmad and Lachlan2, Theorem 3.3]) that this phenomenon is not symmetric: For any two incomparable
${\mathbf a}$
“non-splitting” (i.e., join-irreducible) and thus cannot happen in the c.e. Turing degrees by the Sacks Splitting Theorem [Reference Sacks12].) More interestingly, even Ahmad also showed (see [Reference Ahmad and Lachlan2, Theorem 3.3]) that this phenomenon is not symmetric: For any two incomparable
![]() ${\Sigma ^0_2}$
-enumeration degrees
${\Sigma ^0_2}$
-enumeration degrees
![]() ${\mathbf a}, {\mathbf b}$
, there is either a degree
${\mathbf a}, {\mathbf b}$
, there is either a degree
![]() ${\mathbf x} < {\mathbf a}$
which is
${\mathbf x} < {\mathbf a}$
which is
![]() $\nleq {\mathbf b}$
, or there is a degree
$\nleq {\mathbf b}$
, or there is a degree
![]() ${\mathbf y} < {\mathbf b}$
which is
${\mathbf y} < {\mathbf b}$
which is
![]() $\nleq {\mathbf a}$
.
$\nleq {\mathbf a}$
.
In the language of Question 1.1, Ahmad’s results can be rephrased as stating that not every embedding of an antichain
![]() ${\mathcal P} = \{a,b\}$
can be extended to an embedding of
${\mathcal P} = \{a,b\}$
can be extended to an embedding of
![]() ${\mathcal Q}_0 = \{a,b,x\}$
where
${\mathcal Q}_0 = \{a,b,x\}$
where
![]() $x<a$
and
$x<a$
and
![]() $x \nleq b$
, but that every embedding of
$x \nleq b$
, but that every embedding of
![]() ${\mathcal P}$
can be extended to an embedding of either
${\mathcal P}$
can be extended to an embedding of either
![]() ${\mathcal Q}_0$
or of
${\mathcal Q}_0$
or of
![]() ${\mathcal Q}_1 = \{a,b,y\}$
where
${\mathcal Q}_1 = \{a,b,y\}$
where
![]() $y<b$
and
$y<b$
and
![]() $y \nleq a$
.
$y \nleq a$
.
One of the two main open questions extending the work of the second author, Slaman, and Sorbi [Reference Lempp, Slaman and Sorbi9] asks whether an Ahmad pair of
![]() ${\Sigma ^0_2}$
-enumeration degrees can join to the greatest
${\Sigma ^0_2}$
-enumeration degrees can join to the greatest
![]() ${\Sigma ^0_2}$
-enumeration degree
${\Sigma ^0_2}$
-enumeration degree
![]() ${\mathbf 0}_e'$
. In this paper, we answer this question (communicated to the second author in 2007 by Kent) in the negative:
${\mathbf 0}_e'$
. In this paper, we answer this question (communicated to the second author in 2007 by Kent) in the negative:
Main Theorem. There is no cupping Ahmad pair of
![]() ${\Sigma ^0_2}$
-enumeration degrees
${\Sigma ^0_2}$
-enumeration degrees
![]() $;$
i.e., given any two incomparable
$;$
i.e., given any two incomparable
![]() ${\Sigma ^0_2}$
-enumeration degrees
${\Sigma ^0_2}$
-enumeration degrees
![]() ${\mathbf a}$
and
${\mathbf a}$
and
![]() ${\mathbf b}$
, there is either a
${\mathbf b}$
, there is either a
![]() ${\Sigma ^0_2}$
-enumeration degree
${\Sigma ^0_2}$
-enumeration degree
![]() ${\mathbf x} < {\mathbf a}$
with
${\mathbf x} < {\mathbf a}$
with
![]() ${\mathbf x} \nleq {\mathbf b}$
, or else
${\mathbf x} \nleq {\mathbf b}$
, or else
![]() ${\mathbf a} \cup {\mathbf b} < {\mathbf 0}_e'$
.
${\mathbf a} \cup {\mathbf b} < {\mathbf 0}_e'$
.
This result is a small part of a proposed framework for deciding the
![]() $\forall \exists $
-theory of the
$\forall \exists $
-theory of the
![]() ${\Sigma ^0_2}$
-degrees, which is equivalent to deciding Question 1.1.
${\Sigma ^0_2}$
-degrees, which is equivalent to deciding Question 1.1.
Given the difficulty of the overall problem of deciding the
![]() $\forall \exists $
-theory, researchers are currently concentrating on the following question concerning 1-point extensions:
$\forall \exists $
-theory, researchers are currently concentrating on the following question concerning 1-point extensions:
Question 1.2. Given a finite antichain
![]() ${\mathcal P} = \{a_0, \dots , a_n\}$
and 1-point extensions
${\mathcal P} = \{a_0, \dots , a_n\}$
and 1-point extensions
![]() ${\mathcal Q}_S = \{a_0, \dots , a_n, x_S\}$
and
${\mathcal Q}_S = \{a_0, \dots , a_n, x_S\}$
and
![]() ${\mathcal Q}^T = \{a_0, \dots , a_n, x^T\}$
for some sets
${\mathcal Q}^T = \{a_0, \dots , a_n, x^T\}$
for some sets
![]() $S \in {\mathcal S}$
and
$S \in {\mathcal S}$
and
![]() $T \in {\mathcal T}$
(where
$T \in {\mathcal T}$
(where
![]() ${\mathcal S}, {\mathcal T} \subseteq {\mathcal P}(\{0, \dots , n\}) - \{\emptyset \})$
;
${\mathcal S}, {\mathcal T} \subseteq {\mathcal P}(\{0, \dots , n\}) - \{\emptyset \})$
;
![]() $x_S < a_i$
iff
$x_S < a_i$
iff
![]() $i \in S$
; and
$i \in S$
; and
![]() $x^T> a_i$
iff
$x^T> a_i$
iff
![]() $i \in T$
), does any embedding of
$i \in T$
), does any embedding of
![]() ${\mathcal P}$
into the
${\mathcal P}$
into the
![]() ${\Sigma ^0_2}$
-degrees extend to an embedding into the
${\Sigma ^0_2}$
-degrees extend to an embedding into the
![]() ${\Sigma ^0_2}$
-degrees of
${\Sigma ^0_2}$
-degrees of
![]() ${\mathcal Q}_S$
for some
${\mathcal Q}_S$
for some
![]() $S \in {\mathcal S}$
or to an embedding of
$S \in {\mathcal S}$
or to an embedding of
![]() ${\mathcal Q}^T$
for some
${\mathcal Q}^T$
for some
![]() $T \in {\mathcal T}$
?
$T \in {\mathcal T}$
?
Note that it is always possible to extend an embedding of a finite antichain
![]() ${\mathcal P}$
to an embedding of a larger antichain, so the case
${\mathcal P}$
to an embedding of a larger antichain, so the case
![]() $S = T = \emptyset $
is not interesting. The subproblem involving only extensions
$S = T = \emptyset $
is not interesting. The subproblem involving only extensions
![]() ${\mathcal Q}^T$
is easy to see: We have extendibility iff there is a singleton
${\mathcal Q}^T$
is easy to see: We have extendibility iff there is a singleton
![]() $T \in {\mathcal T}$
.
$T \in {\mathcal T}$
.
Recent work of Goh, the second and third authors, and Soskova [Reference Goh, Ng, Lempp and Soskova4, Reference Goh, Ng, Lempp and Soskova5] gives a complete (and quite complicated) characterization of the subproblem involving only extensions
![]() ${\mathcal Q}_S$
.
${\mathcal Q}_S$
.
We have no working conjecture that combines the
![]() ${\mathcal Q}_S$
and the
${\mathcal Q}_S$
and the
![]() ${\mathcal Q}^T$
; our main result is the only result known to us in this direction.
${\mathcal Q}^T$
; our main result is the only result known to us in this direction.
2 The proof of the Main Theorem
This section is devoted to the proof of our Main Theorem.
2.1 Requirements
Rather than proving the result directly, we use an indirect approach, trying to “weakly split” the degree of A. Specifically, given two
![]() $\Sigma ^0_2$
-sets A and B and an enumeration operator
$\Sigma ^0_2$
-sets A and B and an enumeration operator
![]() $\Lambda $
such that
$\Lambda $
such that
![]() $\overline {K} = \Lambda (A \oplus B)$
(K here denotes the usual Halting set), we construct two sets
$\overline {K} = \Lambda (A \oplus B)$
(K here denotes the usual Halting set), we construct two sets
![]() $X_0 = \Phi _0(A)$
and
$X_0 = \Phi _0(A)$
and
![]() $X_1 = \Phi _1(A)$
with these enumeration operators and an enumeration operator
$X_1 = \Phi _1(A)$
with these enumeration operators and an enumeration operator
![]() $\Gamma $
, and meet the following requirements for all enumeration operators
$\Gamma $
, and meet the following requirements for all enumeration operators
![]() $\Delta $
:
$\Delta $
:
 $$ \begin{align*} \text{Global} &: A=\Gamma(B\oplus X_0\oplus X_1),\\ {\mathcal N}^0_\Delta &: A=\Delta(X_0)\Rightarrow \exists \Omega\,(A=\Omega(B)),\\ {\mathcal N}^1_\Delta &: A=\Delta(X_1)\Rightarrow \exists \Omega\,(A=\Omega(B)). \end{align*} $$
$$ \begin{align*} \text{Global} &: A=\Gamma(B\oplus X_0\oplus X_1),\\ {\mathcal N}^0_\Delta &: A=\Delta(X_0)\Rightarrow \exists \Omega\,(A=\Omega(B)),\\ {\mathcal N}^1_\Delta &: A=\Delta(X_1)\Rightarrow \exists \Omega\,(A=\Omega(B)). \end{align*} $$
Here, the enumeration operators
![]() $\Omega $
are built locally by
$\Omega $
are built locally by
![]() ${\mathcal N}$
-requirements; indeed, as we will see below, each
${\mathcal N}$
-requirements; indeed, as we will see below, each
![]() ${\mathcal N}$
-requirement will build different versions of
${\mathcal N}$
-requirement will build different versions of
![]() $\Omega $
based on different guesses about the higher-priority requirements.
$\Omega $
based on different guesses about the higher-priority requirements.
If we succeed with these requirements, then we have that
![]() $A \le _e B$
, or that
$A \le _e B$
, or that
![]() $X_0, X_1<_e A$
and
$X_0, X_1<_e A$
and
![]() $A \le _e B \oplus X_0 \oplus X_1$
, and so the degrees of A and B clearly cannot form an Ahmad Pair. This corollary is non-uniform in two ways, in that we do not know whether
$A \le _e B \oplus X_0 \oplus X_1$
, and so the degrees of A and B clearly cannot form an Ahmad Pair. This corollary is non-uniform in two ways, in that we do not know whether
![]() $A \le _e B$
or which one (or both) of the
$A \le _e B$
or which one (or both) of the
![]() $X_i$
is not below B, and even assuming
$X_i$
is not below B, and even assuming
![]() $A \not \le _e B$
, we cannot tell uniformly which of
$A \not \le _e B$
, we cannot tell uniformly which of
![]() $X_0$
or
$X_0$
or
![]() $X_1$
(or both) is now below B (in fact, these non-uniformities are unavoidable, as can be shown).
$X_1$
(or both) is now below B (in fact, these non-uniformities are unavoidable, as can be shown).
The construction will be a finite-injury construction. The global requirement should proceed carefully to ensure that we do not end up with a “runaway”
![]() $\Gamma $
-axiom. The other requirements will be ordered in some way in order type
$\Gamma $
-axiom. The other requirements will be ordered in some way in order type
![]() $\omega $
which determines their priority.
$\omega $
which determines their priority.
Our construction uses the Recursion Theorem with Parameters in that we will define “agitators” that we enumerate into the Halting set K, which will then force
![]() $A \oplus B$
to change. More precisely, we assume that we are given an infinite computable list of indices
$A \oplus B$
to change. More precisely, we assume that we are given an infinite computable list of indices
![]() $i_0,i_1,\dots $
for which we are able to define
$i_0,i_1,\dots $
for which we are able to define
![]() $\varphi _{i_y}$
for every y. This allows us to be able to use any of these indices as an “agitator.” For any choice of
$\varphi _{i_y}$
for every y. This allows us to be able to use any of these indices as an “agitator.” For any choice of
![]() ${\mathcal N}$
-requirement, stage s, and potentially numbers a and strings
${\mathcal N}$
-requirement, stage s, and potentially numbers a and strings
![]() $\sigma \in 2^{<\omega }$
, we may define agitators
$\sigma \in 2^{<\omega }$
, we may define agitators
![]() $p_{a,\sigma }$
and q for the
$p_{a,\sigma }$
and q for the
![]() ${\mathcal N}$
-requirement at stage s, picked from the aforementioned list of agitators, and the Recursion Theorem with Parameters allows us to assume that we know what corresponding number will enter K when we enumerate an agitator.
${\mathcal N}$
-requirement at stage s, picked from the aforementioned list of agitators, and the Recursion Theorem with Parameters allows us to assume that we know what corresponding number will enter K when we enumerate an agitator.
2.1.1 Agitators and the use of the Recursion Theorem
We provide more details about agitators and the use of the Recursion Theorem here; the reader who is familiar with this may skip this subsection. As mentioned above, we assume that we are given an infinite computable list of indices
![]() $i_0,i_1,\dots $
for which we are able to control the value of
$i_0,i_1,\dots $
for which we are able to control the value of
![]() $K(i_y)$
for every y. What this means is that for any y, we can assume that
$K(i_y)$
for every y. What this means is that for any y, we can assume that
![]() $i_y\not \in K$
until we choose to enumerate it into K (via making a definition
$i_y\not \in K$
until we choose to enumerate it into K (via making a definition
![]() $\varphi _{i_y}(i_y))$
. If we never choose to enumerate
$\varphi _{i_y}(i_y))$
. If we never choose to enumerate
![]() $i_y$
into K, then it will never appear in
$i_y$
into K, then it will never appear in
![]() $K_s$
for any s; otherwise, if we choose to enumerate it into K, then it must appear in
$K_s$
for any s; otherwise, if we choose to enumerate it into K, then it must appear in
![]() $K_s$
for some large s which we can then wait for by speeding up the approximation to
$K_s$
for some large s which we can then wait for by speeding up the approximation to
![]() $K_s$
.
$K_s$
.
Now it remains to justify the existence of the sequence
![]() $i_0,i_1,\dots $
. To do this, we require the use of the Recursion Theorem with Parameters, applied in the following way. We perform infinitely many constructions, rather than just the one described in the proof, and each construction is given a different label
$i_0,i_1,\dots $
. To do this, we require the use of the Recursion Theorem with Parameters, applied in the following way. We perform infinitely many constructions, rather than just the one described in the proof, and each construction is given a different label
![]() $c\in \omega $
. These constructions are performed uniformly, and each differs only on the assigned label c. In each construction, we build infinitely many partial computable functions
$c\in \omega $
. These constructions are performed uniformly, and each differs only on the assigned label c. In each construction, we build infinitely many partial computable functions
![]() $h_{c,0},h_{c,1},\dots $
representing the list of potential agitators in that construction. The construction will guess that
$h_{c,0},h_{c,1},\dots $
representing the list of potential agitators in that construction. The construction will guess that
![]() $h_{c,y}$
has index
$h_{c,y}$
has index
![]() $\varphi _c(c,y)$
for each y, where c is its assigned label. That is, the construction believes that
$\varphi _c(c,y)$
for each y, where c is its assigned label. That is, the construction believes that
![]() $h_{c,y}=\varphi _{\varphi _c(c,y)}$
for every y. All constructions proceed in exactly the same way, except for its guess on the indices for the sequence
$h_{c,y}=\varphi _{\varphi _c(c,y)}$
for every y. All constructions proceed in exactly the same way, except for its guess on the indices for the sequence
![]() $h_{c,0},h_{c,1},\dots $
. This allows us to use the s-m-n Theorem to obtain a computable function f such that
$h_{c,0},h_{c,1},\dots $
. This allows us to use the s-m-n Theorem to obtain a computable function f such that
![]() $h_{c,y} = \varphi _{f(\varphi _c(c,y),c,y)}$
for every c and y. The Recursion Theorem with Parameters gives an index c such that
$h_{c,y} = \varphi _{f(\varphi _c(c,y),c,y)}$
for every c and y. The Recursion Theorem with Parameters gives an index c such that
![]() $h_{c,y}=\varphi _{f(\varphi _c(c,y),c,y)}=\varphi _{\varphi _c(c,y)}$
holds for every y. Now the construction which was assigned label c will have the correct guesses on the indices of the agitators.
$h_{c,y}=\varphi _{f(\varphi _c(c,y),c,y)}=\varphi _{\varphi _c(c,y)}$
holds for every y. Now the construction which was assigned label c will have the correct guesses on the indices of the agitators.
2.2 Basic strategies for the requirements
We fix a computable enumeration
![]() $\{K_s\}$
of K, and let
$\{K_s\}$
of K, and let
![]() $\overline {K}_s$
be the complement of
$\overline {K}_s$
be the complement of
![]() $K_s$
. By speeding up the enumeration of
$K_s$
. By speeding up the enumeration of
![]() $\Lambda $
and the approximations to A and B, we may assume at any stage s that for all numbers
$\Lambda $
and the approximations to A and B, we may assume at any stage s that for all numbers
![]() $p<s$
, if
$p<s$
, if
![]() $p \in \overline {K}_s$
, then currently
$p \in \overline {K}_s$
, then currently
![]() $p \in \Lambda (A \oplus B)$
, and if
$p \in \Lambda (A \oplus B)$
, and if
![]() $p \notin \overline {K}_s$
, then any axiom putting p into
$p \notin \overline {K}_s$
, then any axiom putting p into
![]() $\Lambda (A \oplus B)$
at stage
$\Lambda (A \oplus B)$
at stage
![]() $s-1$
will no longer apply at stage s.
$s-1$
will no longer apply at stage s.
The global requirement constructing the operator
![]() $\Gamma $
will enumerate axioms into
$\Gamma $
will enumerate axioms into
![]() $\Gamma $
taking into account more and more of the other requirements’ action; the basic action of the global requirement is to just enumerate an axiom for a into
$\Gamma $
taking into account more and more of the other requirements’ action; the basic action of the global requirement is to just enumerate an axiom for a into
![]() $\Gamma $
whenever it sees a enter A. Specifically, for each
$\Gamma $
whenever it sees a enter A. Specifically, for each
![]() $a \in A$
, we associate with a fresh numbers
$a \in A$
, we associate with a fresh numbers
![]() $c^i_a>a$
targeted for
$c^i_a>a$
targeted for
![]() $X_i$
for
$X_i$
for
![]() $i<2$
; we then enumerate
$i<2$
; we then enumerate
![]() $c^i_a$
into
$c^i_a$
into
![]() $X_i$
via the
$X_i$
via the
![]() $\Phi _i$
-axioms
$\Phi _i$
-axioms
![]() $\langle c^i_a,\{a\} \rangle $
, and we enumerate a new axiom
$\langle c^i_a,\{a\} \rangle $
, and we enumerate a new axiom
![]() $\langle a,B_a \oplus C^0_a \oplus C^1_a \rangle $
into
$\langle a,B_a \oplus C^0_a \oplus C^1_a \rangle $
into
![]() $\Gamma $
where
$\Gamma $
where
![]() $B_a$
is some finite subset of B, and
$B_a$
is some finite subset of B, and
![]() $C^i_a$
is a finite subset of
$C^i_a$
is a finite subset of
![]() $X_i$
containing
$X_i$
containing
![]() $c^i_a$
and possibly other numbers determined later; this will result in
$c^i_a$
and possibly other numbers determined later; this will result in
![]() $a \in \Gamma (B \oplus X_0 \oplus X_1)$
. Now, when a leaves A, this will remove
$a \in \Gamma (B \oplus X_0 \oplus X_1)$
. Now, when a leaves A, this will remove
![]() $c^0_a$
from
$c^0_a$
from
![]() $X_0$
and
$X_0$
and
![]() $c^1_a$
from
$c^1_a$
from
![]() $X_1$
unless we introduce additional axioms for either of these numbers. (More generally, ensuring
$X_1$
unless we introduce additional axioms for either of these numbers. (More generally, ensuring
![]() $C^0_a \not \subseteq X_0$
or
$C^0_a \not \subseteq X_0$
or
![]() $C^1_a \not \subseteq X_1$
or
$C^1_a \not \subseteq X_1$
or
![]() $B_a \not \subseteq B$
would suffice, as will be required later.)
$B_a \not \subseteq B$
would suffice, as will be required later.)
The basic strategy for the
![]() ${\mathcal N}^i_\Delta $
-requirement is to try to show that
${\mathcal N}^i_\Delta $
-requirement is to try to show that
![]() $A = \Omega (B)$
as follows: At each stage, the
$A = \Omega (B)$
as follows: At each stage, the
![]() ${\mathcal N}^i_\Delta $
-requirement determines the oldest
${\mathcal N}^i_\Delta $
-requirement determines the oldest
![]() $a \in A$
(if any) which has not yet been confirmed (as defined precisely below) and checks if there is currently some F such that
$a \in A$
(if any) which has not yet been confirmed (as defined precisely below) and checks if there is currently some F such that
![]() $a \in \Delta (F)$
; if no such F exists, the requirement does nothing for now. If there is such F, the requirement declares a to be confirmed and dumps all
$a \in \Delta (F)$
; if no such F exists, the requirement does nothing for now. If there is such F, the requirement declares a to be confirmed and dumps all
![]() $x \in F$
into
$x \in F$
into
![]() $X_i$
by enumerating axioms
$X_i$
by enumerating axioms
![]() $\langle x,\emptyset \rangle $
into
$\langle x,\emptyset \rangle $
into
![]() $\Phi _i$
(and thus ensures that
$\Phi _i$
(and thus ensures that
![]() $a \in \Delta (X_i)$
permanently); it also chooses a fresh agitator
$a \in \Delta (X_i)$
permanently); it also chooses a fresh agitator
![]() $p_a$
, keeps
$p_a$
, keeps
![]() $p_a \in \overline {K}$
for now, and waits for
$p_a \in \overline {K}$
for now, and waits for
![]() $p_a \in \Lambda (A \oplus B)$
(which must happen by the first stage
$p_a \in \Lambda (A \oplus B)$
(which must happen by the first stage
![]() $s>p_a$
) via a
$s>p_a$
) via a
![]() $\Lambda $
-axiom
$\Lambda $
-axiom
![]() $\langle p_a,F_a \oplus G_a \rangle $
, say, for which all
$\langle p_a,F_a \oplus G_a \rangle $
, say, for which all
![]() $a' \in F_a$
have been confirmed already (which need not ever happen). The
$a' \in F_a$
have been confirmed already (which need not ever happen). The
![]() ${\mathcal N}^i_\Delta $
-requirement then enumerates a into
${\mathcal N}^i_\Delta $
-requirement then enumerates a into
![]() $\Omega (B)$
via the
$\Omega (B)$
via the
![]() $\Omega $
-axiom
$\Omega $
-axiom
![]() $\langle a,G_a \rangle $
. If
$\langle a,G_a \rangle $
. If
![]() $p_a$
leaves
$p_a$
leaves
![]() $\Lambda (A \oplus B)$
before we enumerate
$\Lambda (A \oplus B)$
before we enumerate
![]() $p_a$
into K (if ever), then we wait again for a to re-enter
$p_a$
into K (if ever), then we wait again for a to re-enter
![]() $\Lambda (A \oplus B)$
via a possibly different
$\Lambda (A \oplus B)$
via a possibly different
![]() $\Lambda $
-axiom
$\Lambda $
-axiom
![]() $\langle p_a,F^{\prime }_a \oplus G^{\prime }_a \rangle $
(such that again all
$\langle p_a,F^{\prime }_a \oplus G^{\prime }_a \rangle $
(such that again all
![]() $a' \in F^{\prime }_a$
are confirmed); then we will use the (possibly different) set
$a' \in F^{\prime }_a$
are confirmed); then we will use the (possibly different) set
![]() $G^{\prime }_a$
in redefining
$G^{\prime }_a$
in redefining
![]() $a \in \Omega (B)$
, etc.; this can happen only finitely often for this fixed
$a \in \Omega (B)$
, etc.; this can happen only finitely often for this fixed
![]() $p_a$
. If a leaves A after a is confirmed, then we enumerate the current agitator
$p_a$
. If a leaves A after a is confirmed, then we enumerate the current agitator
![]() $p_a$
into K; if later a re-enters A, then we pick a new, fresh agitator
$p_a$
into K; if later a re-enters A, then we pick a new, fresh agitator
![]() $p^{\prime }_a$
, say, for which we proceed as above (finding sets
$p^{\prime }_a$
, say, for which we proceed as above (finding sets
![]() $F^{\prime }_a$
and
$F^{\prime }_a$
and
![]() $G^{\prime }_a$
and enumerating an
$G^{\prime }_a$
and enumerating an
![]() $\Omega $
-axiom
$\Omega $
-axiom
![]() $\langle a,G^{\prime }_a \rangle $
, etc.). From now on, whenever some agitator
$\langle a,G^{\prime }_a \rangle $
, etc.). From now on, whenever some agitator
![]() $p_a \in K$
and for any corresponding set
$p_a \in K$
and for any corresponding set
![]() $G_a$
, we see
$G_a$
, we see
![]() $G_a \subseteq B$
, then the
$G_a \subseteq B$
, then the
![]() ${\mathcal N}^i_\Delta $
-requirement stops (since it believes that
${\mathcal N}^i_\Delta $
-requirement stops (since it believes that
![]() $F_a \not \subseteq A$
while
$F_a \not \subseteq A$
while
![]() $F_a \subseteq \Delta (X_i)$
by dumping). Note that if a is truly in A, then the final agitator
$F_a \subseteq \Delta (X_i)$
by dumping). Note that if a is truly in A, then the final agitator
![]() $p_a$
for a will stabilize and be in
$p_a$
for a will stabilize and be in
![]() $\overline {K}$
; on the other hand, if
$\overline {K}$
; on the other hand, if
![]() $a \notin A$
then a will either appear to be outside A at cofinitely many stages, or the agitator will never stabilize, and any temporary agitator
$a \notin A$
then a will either appear to be outside A at cofinitely many stages, or the agitator will never stabilize, and any temporary agitator
![]() $p_a$
will eventually be in K.
$p_a$
will eventually be in K.
We need to check two things: First of all, note that the
![]() ${\mathcal N}^i_\Delta $
-requirement can act only finitely often unless
${\mathcal N}^i_\Delta $
-requirement can act only finitely often unless
![]() $A = \Omega (B)$
(which would contradict our hypotheses): If the requirement acts for the sake of infinitely many distinct a, then, since we always choose a by age, we will have for each
$A = \Omega (B)$
(which would contradict our hypotheses): If the requirement acts for the sake of infinitely many distinct a, then, since we always choose a by age, we will have for each
![]() $a \in A$
that a will be confirmed and that
$a \in A$
that a will be confirmed and that
![]() $a \in \Omega (B)$
by an axiom using the final agitator
$a \in \Omega (B)$
by an axiom using the final agitator
![]() $p_a \in \overline {K}$
and the B-part
$p_a \in \overline {K}$
and the B-part
![]() $G_a$
of its
$G_a$
of its
![]() $\Lambda $
-use; and for each
$\Lambda $
-use; and for each
![]() $a \notin A$
we will have that
$a \notin A$
we will have that
![]() $a \notin \Omega (B)$
since no
$a \notin \Omega (B)$
since no
![]() $\Omega $
-axiom can apply: If
$\Omega $
-axiom can apply: If
![]() $a \in \Omega (B)$
via some axiom
$a \in \Omega (B)$
via some axiom
![]() $\langle a,G_a \rangle $
, say, but
$\langle a,G_a \rangle $
, say, but
![]() $a \notin A$
, then
$a \notin A$
, then
![]() $G_a$
is the B-part of the
$G_a$
is the B-part of the
![]() $\Lambda $
-use of some agitator
$\Lambda $
-use of some agitator
![]() $p_a$
, but every such agitator
$p_a$
, but every such agitator
![]() $p_a$
will be enumerated into K and thus
$p_a$
will be enumerated into K and thus
![]() $G_a \subseteq B$
will eventually stop the
$G_a \subseteq B$
will eventually stop the
![]() ${\mathcal N}^i_\Delta $
-requirement permanently. On the other hand, the
${\mathcal N}^i_\Delta $
-requirement permanently. On the other hand, the
![]() ${\mathcal N}^i_\Delta $
-requirement cannot act infinitely often for some fixed
${\mathcal N}^i_\Delta $
-requirement cannot act infinitely often for some fixed
![]() $a_0$
since that would mean that
$a_0$
since that would mean that
![]() $a_0 \notin A$
and so the age of
$a_0 \notin A$
and so the age of
![]() $a_0$
would keep increasing and we would choose other numbers infinitely often (assuming here, of course, that A is infinite).
$a_0$
would keep increasing and we would choose other numbers infinitely often (assuming here, of course, that A is infinite).
The second item we need to check is that the
![]() ${\mathcal N}^i_\Delta $
-requirement satisfies its requirement, so assume that indeed
${\mathcal N}^i_\Delta $
-requirement satisfies its requirement, so assume that indeed
![]() $A = \Delta (X_i)$
: Then every a truly in A must be confirmed eventually, but since we may assume A to be infinite, this means that the
$A = \Delta (X_i)$
: Then every a truly in A must be confirmed eventually, but since we may assume A to be infinite, this means that the
![]() ${\mathcal N}^i_\Delta $
-requirement acts infinitely often and thus ensures
${\mathcal N}^i_\Delta $
-requirement acts infinitely often and thus ensures
![]() $A = \Omega (B)$
as shown in the previous paragraph.
$A = \Omega (B)$
as shown in the previous paragraph.
2.3 Conflicts between the
 ${\mathcal N}$
-requirements and the global requirement
${\mathcal N}$
-requirements and the global requirement
A single
![]() ${\mathcal N}^i$
-requirement will not conflict with the global requirement building and correcting
${\mathcal N}^i$
-requirement will not conflict with the global requirement building and correcting
![]() $\Gamma $
since when a leaves A,
$\Gamma $
since when a leaves A,
![]() $\Gamma $
can always be corrected by extracting
$\Gamma $
can always be corrected by extracting
![]() $c^{1-i}_a$
from
$c^{1-i}_a$
from
![]() $X_{1-i}$
(as no requirement has dumped that number into
$X_{1-i}$
(as no requirement has dumped that number into
![]() $X_{1-i}$
so far).
$X_{1-i}$
so far).
So let’s consider the case of a higher-priority
![]() ${\mathcal N}^0$
-requirement above a lower-priority
${\mathcal N}^0$
-requirement above a lower-priority
![]() ${\mathcal N}^1$
-requirement: The main difficulty is that any number
${\mathcal N}^1$
-requirement: The main difficulty is that any number
![]() $x_0$
dumped by the
$x_0$
dumped by the
![]() ${\mathcal N}^0$
-requirement is associated with some number a potentially in A, which in turn may be associated with a number
${\mathcal N}^0$
-requirement is associated with some number a potentially in A, which in turn may be associated with a number
![]() $x_1$
that the
$x_1$
that the
![]() ${\mathcal N}^1$
-requirement may dump into
${\mathcal N}^1$
-requirement may dump into
![]() $X_1$
, so if both
$X_1$
, so if both
![]() $x_0$
and
$x_0$
and
![]() $x_1$
are dumped, then we may not be able to correct
$x_1$
are dumped, then we may not be able to correct
![]() $\Gamma (B \oplus X_0 \oplus X_1)$
if a leaves A, injuring the global requirement.
$\Gamma (B \oplus X_0 \oplus X_1)$
if a leaves A, injuring the global requirement.
So the
![]() ${\mathcal N}^1$
-requirement, assuming that the
${\mathcal N}^1$
-requirement, assuming that the
![]() ${\mathcal N}^0$
-requirement acts only finitely often, will be modified as follows: Each time the
${\mathcal N}^0$
-requirement acts only finitely often, will be modified as follows: Each time the
![]() ${\mathcal N}^0$
-requirement acts, the
${\mathcal N}^0$
-requirement acts, the
![]() ${\mathcal N}^1$
-requirement’s action will be completely undone by enumerating an agitator q (chosen by the
${\mathcal N}^1$
-requirement’s action will be completely undone by enumerating an agitator q (chosen by the
![]() ${\mathcal N}^0$
-requirement) into K, which will force an
${\mathcal N}^0$
-requirement) into K, which will force an
![]() $(A \oplus B)$
-change undoing all
$(A \oplus B)$
-change undoing all
![]() $\Gamma $
-axioms enumerated since the
$\Gamma $
-axioms enumerated since the
![]() ${\mathcal N}^0$
-requirement was last active (and thus any
${\mathcal N}^0$
-requirement was last active (and thus any
![]() $\Gamma $
-axioms enumerated while the
$\Gamma $
-axioms enumerated while the
![]() ${\mathcal N}^1$
-requirement was active since then), where
${\mathcal N}^1$
-requirement was active since then), where
![]() $q \in \Lambda (A \oplus B)$
via a
$q \in \Lambda (A \oplus B)$
via a
![]() $\Lambda $
-axiom
$\Lambda $
-axiom
![]() $\langle q,F_q \oplus G_q \rangle $
, say; now the numbers in
$\langle q,F_q \oplus G_q \rangle $
, say; now the numbers in
![]() $F_q$
are associated with sets of numbers
$F_q$
are associated with sets of numbers
![]() $F^i_q$
in
$F^i_q$
in
![]() $X_i$
for
$X_i$
for
![]() $i<2$
, and so we may assume that each
$i<2$
, and so we may assume that each
![]() $\Gamma $
-axiom enumerated since the
$\Gamma $
-axiom enumerated since the
![]() ${\mathcal N}^0$
-requirement was last active contains
${\mathcal N}^0$
-requirement was last active contains
![]() $B_q \oplus C^0_q \oplus C^1_q$
in its use; thus we will now ensure that when q enters K, this will entail
$B_q \oplus C^0_q \oplus C^1_q$
in its use; thus we will now ensure that when q enters K, this will entail
![]() $B_q \oplus C^0_q \oplus C^1_q \not \subseteq B \oplus X_0 \oplus X_1$
. This feature will thus prevent the
$B_q \oplus C^0_q \oplus C^1_q \not \subseteq B \oplus X_0 \oplus X_1$
. This feature will thus prevent the
![]() ${\mathcal N}^1$
-requirement from interfering with the global requirement as long as the
${\mathcal N}^1$
-requirement from interfering with the global requirement as long as the
![]() ${\mathcal N}^1$
-requirement cannot unconditionally dump numbers into
${\mathcal N}^1$
-requirement cannot unconditionally dump numbers into
![]() $X_1$
like the
$X_1$
like the
![]() ${\mathcal N}^0$
-requirement.
${\mathcal N}^0$
-requirement.
In addition to this extra initialization, we will now modify the strategy for the
![]() ${\mathcal N}^1$
-requirement as follows: Let r be a strict bound on the largest number ever considered by the
${\mathcal N}^1$
-requirement as follows: Let r be a strict bound on the largest number ever considered by the
![]() ${\mathcal N}^0$
-requirement up to this stage, and assume that this bound is reset each time the computation for
${\mathcal N}^0$
-requirement up to this stage, and assume that this bound is reset each time the computation for
![]() $q \in \Lambda (A \oplus B)$
changes. (If the
$q \in \Lambda (A \oplus B)$
changes. (If the
![]() ${\mathcal N}^0$
-requirement acts only finitely often, then this number will stabilize eventually.)
${\mathcal N}^0$
-requirement acts only finitely often, then this number will stabilize eventually.)
The
![]() ${\mathcal N}^1$
-requirement will now be prevented from making any changes to
${\mathcal N}^1$
-requirement will now be prevented from making any changes to
![]() $X_1$
at any number
$X_1$
at any number
![]() $<r$
and will work with all possible guesses
$<r$
and will work with all possible guesses
![]() $\sigma \in 2^r$
about
$\sigma \in 2^r$
about
![]() $A {\,\upharpoonright \,} r$
. (Recall here that any number x potentially in
$A {\,\upharpoonright \,} r$
. (Recall here that any number x potentially in
![]() $X_1$
is associated with a number
$X_1$
is associated with a number
![]() $a<x$
potentially in A, or with no number at all, so a guess about
$a<x$
potentially in A, or with no number at all, so a guess about
![]() $A {\,\upharpoonright \,} r$
will eventually give complete information about
$A {\,\upharpoonright \,} r$
will eventually give complete information about
![]() $X_1 {\,\upharpoonright \,} r$
.) Each version of the strategy for the
$X_1 {\,\upharpoonright \,} r$
.) Each version of the strategy for the
![]() ${\mathcal N}^1$
-requirement (let’s call it the
${\mathcal N}^1$
-requirement (let’s call it the
![]() ${\mathcal N}^1_\sigma $
-strategy) will build its own version of the enumeration operator
${\mathcal N}^1_\sigma $
-strategy) will build its own version of the enumeration operator
![]() $\Omega $
(call it
$\Omega $
(call it
![]() $\Omega _\sigma $
); each
$\Omega _\sigma $
); each
![]() ${\mathcal N}^1_\sigma $
-strategy will now act independently, building not only its own
${\mathcal N}^1_\sigma $
-strategy will now act independently, building not only its own
![]() $\Omega _\sigma $
but also define its own agitators
$\Omega _\sigma $
but also define its own agitators
![]() $p_a = p_{a,\sigma }$
. (On the other hand, the agitator q is attached to an entire requirement and so can be joint for all
$p_a = p_{a,\sigma }$
. (On the other hand, the agitator q is attached to an entire requirement and so can be joint for all
![]() ${\mathcal N}$
-strategies working for the same requirement since this is a finite-injury argument.)
${\mathcal N}$
-strategies working for the same requirement since this is a finite-injury argument.)
Each
![]() ${\mathcal N}^1_\sigma $
-strategy will then, instead of dumping a number
${\mathcal N}^1_\sigma $
-strategy will then, instead of dumping a number
![]() $x<r$
into
$x<r$
into
![]() $X_1$
, simply check if its guess about
$X_1$
, simply check if its guess about
![]() $A {\,\upharpoonright \,} r$
and about
$A {\,\upharpoonright \,} r$
and about
![]() $\Phi _1$
puts x into
$\Phi _1$
puts x into
![]() $X_1$
, and this guess will eventually be correct about each such x; for numbers
$X_1$
, and this guess will eventually be correct about each such x; for numbers
![]() $x \ge r$
, the
$x \ge r$
, the
![]() ${\mathcal N}^1_\sigma $
-strategy can still simply “dump” numbers into
${\mathcal N}^1_\sigma $
-strategy can still simply “dump” numbers into
![]() $X_1$
but only with the set
$X_1$
but only with the set
![]() $F_q$
(from the
$F_q$
(from the
![]() $\Lambda $
-axiom
$\Lambda $
-axiom
![]() $\langle q, F_q \oplus G_q \rangle $
) in the A-part of the
$\langle q, F_q \oplus G_q \rangle $
) in the A-part of the
![]() $\Phi _1$
-use. (Also, the strategy will stop if it sees a number
$\Phi _1$
-use. (Also, the strategy will stop if it sees a number
![]() $a \in A {\,\upharpoonright \,} r$
with
$a \in A {\,\upharpoonright \,} r$
with
![]() $\sigma (a)=0$
.) Note that this is sufficient to allow the global strategy to correct
$\sigma (a)=0$
.) Note that this is sufficient to allow the global strategy to correct
![]() $\Gamma $
whenever necessary: If any number a leaves A, then the global strategy can either use
$\Gamma $
whenever necessary: If any number a leaves A, then the global strategy can either use
![]() $X_0$
to correct
$X_0$
to correct
![]() $\Gamma $
if the
$\Gamma $
if the
![]() $\Gamma $
-axiom for
$\Gamma $
-axiom for
![]() $a \in \Gamma (B \oplus X_0 \oplus X_1)$
was defined after the stage
$a \in \Gamma (B \oplus X_0 \oplus X_1)$
was defined after the stage
![]() $s_r$
, say, at which the
$s_r$
, say, at which the
![]() ${\mathcal N}^0$
-requirement last acted (since no strategy will have dumped any number
${\mathcal N}^0$
-requirement last acted (since no strategy will have dumped any number
![]() $\ge r$
into
$\ge r$
into
![]() $X_0$
up to this point), or it can use
$X_0$
up to this point), or it can use
![]() $X_1$
or B if the
$X_1$
or B if the
![]() $\Gamma $
-axiom for
$\Gamma $
-axiom for
![]() $a \in \Gamma (B \oplus X_0 \oplus X_1)$
was defined before stage
$a \in \Gamma (B \oplus X_0 \oplus X_1)$
was defined before stage
![]() $s_r$
(since any number dumped into
$s_r$
(since any number dumped into
![]() $X_1$
before stage
$X_1$
before stage
![]() $s_r$
must have been dumped by an
$s_r$
must have been dumped by an
![]() ${\mathcal N}^1_\sigma $
-strategy before r was last increased, and thus the corresponding agitator q of the
${\mathcal N}^1_\sigma $
-strategy before r was last increased, and thus the corresponding agitator q of the
![]() ${\mathcal N}^0$
-requirement from that time was enumerated into K, resulting in a B-change, or in an A- and thus an
${\mathcal N}^0$
-requirement from that time was enumerated into K, resulting in a B-change, or in an A- and thus an
![]() $X_0$
-change, invalidating any
$X_0$
-change, invalidating any
![]() $\Gamma $
-axiom for a that might involve a number dumped by an
$\Gamma $
-axiom for a that might involve a number dumped by an
![]() ${\mathcal N}^1_\sigma $
-strategy in its use).
${\mathcal N}^1_\sigma $
-strategy in its use).
We now have to verify two things: Firstly, the
![]() ${\mathcal N}^1_\sigma $
-strategy with the correct guess
${\mathcal N}^1_\sigma $
-strategy with the correct guess
![]() $\sigma = A {\,\upharpoonright \,} r$
will ensure the satisfaction of the
$\sigma = A {\,\upharpoonright \,} r$
will ensure the satisfaction of the
![]() ${\mathcal N}^1$
-requirement. And secondly, any
${\mathcal N}^1$
-requirement. And secondly, any
![]() ${\mathcal N}^1_\sigma $
-strategy will act at most finitely often even if its guess
${\mathcal N}^1_\sigma $
-strategy will act at most finitely often even if its guess
![]() $\sigma $
about
$\sigma $
about
![]() $A {\,\upharpoonright \,} r$
is incorrect.
$A {\,\upharpoonright \,} r$
is incorrect.
So suppose first that r is the final value of this parameter and fix
![]() $\sigma = A {\,\upharpoonright \,} r$
. Then, starting at some stage
$\sigma = A {\,\upharpoonright \,} r$
. Then, starting at some stage
![]() $s_r$
, any number
$s_r$
, any number
![]() $x \in X_1 {\,\upharpoonright \,} r$
will forever be in
$x \in X_1 {\,\upharpoonright \,} r$
will forever be in
![]() $X_1 = \Phi _1(A)$
. So starting at stage
$X_1 = \Phi _1(A)$
. So starting at stage
![]() $s_r$
, the
$s_r$
, the
![]() ${\mathcal N}^1_\sigma $
-strategy can act like the
${\mathcal N}^1_\sigma $
-strategy can act like the
![]() ${\mathcal N}$
-strategy in isolation except that it cannot dump any number
${\mathcal N}$
-strategy in isolation except that it cannot dump any number
![]() $x<r$
into
$x<r$
into
![]() $X_1$
, but no such number will be truly in
$X_1$
, but no such number will be truly in
![]() $X_1$
unless it is so by stage
$X_1$
unless it is so by stage
![]() $s_r$
, so this does not cause more than finitely many mistakes for
$s_r$
, so this does not cause more than finitely many mistakes for
![]() $\Omega _\sigma $
in case the
$\Omega _\sigma $
in case the
![]() ${\mathcal N}^1_\sigma $
-strategy acts infinitely often.
${\mathcal N}^1_\sigma $
-strategy acts infinitely often.
Next, fix any
![]() ${\mathcal N}^1_\sigma $
-strategy (irrespective of whether
${\mathcal N}^1_\sigma $
-strategy (irrespective of whether
![]() $\sigma = A {\,\upharpoonright \,} r$
or not). In order to show that this strategy acts at most finitely often, we distinguish two cases: If
$\sigma = A {\,\upharpoonright \,} r$
or not). In order to show that this strategy acts at most finitely often, we distinguish two cases: If
![]() $A {\,\upharpoonright \,} r \not \subseteq \sigma $
, fix the oldest element
$A {\,\upharpoonright \,} r \not \subseteq \sigma $
, fix the oldest element
![]() $a \in A {\,\upharpoonright \,} r$
with
$a \in A {\,\upharpoonright \,} r$
with
![]() $\sigma (a)=0$
; in that case, the strategy clearly stops as soon as a no longer leaves A. On the other hand, if
$\sigma (a)=0$
; in that case, the strategy clearly stops as soon as a no longer leaves A. On the other hand, if
![]() $A {\,\upharpoonright \,} r \subseteq \sigma $
, then the strategy will act as in isolation (since it will never want to dump a number into
$A {\,\upharpoonright \,} r \subseteq \sigma $
, then the strategy will act as in isolation (since it will never want to dump a number into
![]() $X_1$
that it cannot dump) and so must also eventually stop unless
$X_1$
that it cannot dump) and so must also eventually stop unless
![]() $A \le _e B$
.
$A \le _e B$
.
This concludes the presentation of the intuition behind our construction; we are now ready to describe it formally in full.
2.4 The full construction
Recall that we are given approximations to
![]() $\Sigma ^0_2$
-sets A and B and an enumeration operator
$\Sigma ^0_2$
-sets A and B and an enumeration operator
![]() $\Lambda $
such that at any stage s, for any number
$\Lambda $
such that at any stage s, for any number
![]() $p<s$
, if
$p<s$
, if
![]() $p \in \overline {K}_s$
then
$p \in \overline {K}_s$
then
![]() $p \in \Lambda (A \oplus B)[s]$
, and if
$p \in \Lambda (A \oplus B)[s]$
, and if
![]() $p \in K_s$
then p is not in both
$p \in K_s$
then p is not in both
![]() $\Lambda (A \oplus B)[s-1]$
and
$\Lambda (A \oplus B)[s-1]$
and
![]() $\Lambda (A \oplus B)[s]$
via the same axiom. Furthermore, we may assume to be given a good approximation
$\Lambda (A \oplus B)[s]$
via the same axiom. Furthermore, we may assume to be given a good approximation
![]() $\{A_s \oplus B_s\}_{s \in \omega }$
(of finite sets) to
$\{A_s \oplus B_s\}_{s \in \omega }$
(of finite sets) to
![]() $A \oplus B$
, i.e., there are infinitely many true stages, namely, stages s with
$A \oplus B$
, i.e., there are infinitely many true stages, namely, stages s with
![]() $A_s \oplus B_s \subseteq A \oplus B$
.
$A_s \oplus B_s \subseteq A \oplus B$
.
Since we have a finite-injury construction with one global requirement, the action at each stage s will consist of a single action for the highest-priority
![]() ${\mathcal N}$
-requirement requiring attention, followed by some global action. At stage 0, all
${\mathcal N}$
-requirement requiring attention, followed by some global action. At stage 0, all
![]() ${\mathcal N}$
-requirements are initialized and all functionals and agitators are set to be undefined.
${\mathcal N}$
-requirements are initialized and all functionals and agitators are set to be undefined.
We say that an
![]() ${\mathcal N}^i_{\Delta ,\sigma }$
-strategy (for
${\mathcal N}^i_{\Delta ,\sigma }$
-strategy (for
![]() $\sigma \in 2^r$
and some
$\sigma \in 2^r$
and some
![]() $r \in \omega $
) requires attention if:
$r \in \omega $
) requires attention if:
-
• there is no
 $a \in A_s {\,\upharpoonright \,} r$
with
$a \in A_s {\,\upharpoonright \,} r$
with
 $\sigma (a)=0$
; and
$\sigma (a)=0$
; and -
• there is no agitator
 $p_a \in K_s$
with
$p_a \in K_s$
with
 $G_a \subseteq B_s$
for the corresponding
$G_a \subseteq B_s$
for the corresponding
 $\Lambda $
-axiom
$\Lambda $
-axiom
 $\langle p_a, F_a \oplus G_a \rangle $
where
$\langle p_a, F_a \oplus G_a \rangle $
where
 $p_a = p_{a,\sigma '}$
is any agitator ever used by an
$p_a = p_{a,\sigma '}$
is any agitator ever used by an
 ${\mathcal N}^i_{\Delta ,\sigma '}$
-strategy working for the same
${\mathcal N}^i_{\Delta ,\sigma '}$
-strategy working for the same
 ${\mathcal N}^i_\Delta $
-requirement; and
${\mathcal N}^i_\Delta $
-requirement; and -
• one of the following four conditions holds:
-
(1) there is some
 $a \in \Omega (B)[s] - A_s$
(with the oldest
$a \in \Omega (B)[s] - A_s$
(with the oldest
 $\Omega $
-axiom applicable); or
$\Omega $
-axiom applicable); or -
(2) there is some (oldest)
 $a \in A_s - \Omega (B)[s]$
which has already been confirmed by the
$a \in A_s - \Omega (B)[s]$
which has already been confirmed by the
 ${\mathcal N}^i_{\Delta ,\sigma }$
-strategy (since its last initialization) via F, say, and each
${\mathcal N}^i_{\Delta ,\sigma }$
-strategy (since its last initialization) via F, say, and each
 $a' \in F$
has also already been confirmed by the
$a' \in F$
has also already been confirmed by the
 ${\mathcal N}^i_{\Delta ,\sigma }$
-strategy (since its last initialization); or
${\mathcal N}^i_{\Delta ,\sigma }$
-strategy (since its last initialization); or -
(3) there is some (oldest)
 $a \in A_s$
which has not yet been confirmed by the
$a \in A_s$
which has not yet been confirmed by the
 ${\mathcal N}^i_{\Delta ,\sigma }$
-strategy (since its last initialization) and for which there is a finite set F (of least canonical index) with
${\mathcal N}^i_{\Delta ,\sigma }$
-strategy (since its last initialization) and for which there is a finite set F (of least canonical index) with
 $F {\,\upharpoonright \,} r = \Phi _i(\sigma ) {\,\upharpoonright \,} r$
and
$F {\,\upharpoonright \,} r = \Phi _i(\sigma ) {\,\upharpoonright \,} r$
and
 $a \in \Delta _s(F)$
; or
$a \in \Delta _s(F)$
; or -
(4) all the strategies for this
 ${\mathcal N}$
-requirement have not acted since they were last initialized.
${\mathcal N}$
-requirement have not acted since they were last initialized.
-
If an
![]() ${\mathcal N}^i_{\Delta ,\sigma }$
-strategy requires attention, we also say that the corresponding
${\mathcal N}^i_{\Delta ,\sigma }$
-strategy requires attention, we also say that the corresponding
![]() ${\mathcal N}^i_\Delta $
-requirement requires attention.
${\mathcal N}^i_\Delta $
-requirement requires attention.
At a stage
![]() $s>0$
, we first check if there is a (highest-priority)
$s>0$
, we first check if there is a (highest-priority)
![]() ${\mathcal N}^i_\Delta $
-requirement requiring attention; if so, allow all
${\mathcal N}^i_\Delta $
-requirement requiring attention; if so, allow all
![]() ${\mathcal N}^i_{\Delta ,\sigma }$
-strategies working for this
${\mathcal N}^i_{\Delta ,\sigma }$
-strategies working for this
![]() ${\mathcal N}^i_\Delta $
-requirement to act if they require attention. Each such
${\mathcal N}^i_\Delta $
-requirement to act if they require attention. Each such
![]() ${\mathcal N}^i_{\Delta ,\sigma }$
-strategy will now act according to the first clause of the third bullet that applies.
${\mathcal N}^i_{\Delta ,\sigma }$
-strategy will now act according to the first clause of the third bullet that applies.
If (1) applies, then the
![]() ${\mathcal N}^i_{\Delta ,\sigma }$
-strategy enumerates into K the agitator
${\mathcal N}^i_{\Delta ,\sigma }$
-strategy enumerates into K the agitator
![]() $p_a = p_{a,\sigma }$
which was chosen when the current
$p_a = p_{a,\sigma }$
which was chosen when the current
![]() $\Omega _\sigma $
-axiom for
$\Omega _\sigma $
-axiom for
![]() $a \in \Omega _\sigma (B)$
was defined. (Note that
$a \in \Omega _\sigma (B)$
was defined. (Note that
![]() $p_a \notin K_s$
since otherwise, the second bullet would have prevented the
$p_a \notin K_s$
since otherwise, the second bullet would have prevented the
![]() ${\mathcal N}^i_\Delta $
-requirement from requiring attention.)
${\mathcal N}^i_\Delta $
-requirement from requiring attention.)
If (2) applies, then the
![]() ${\mathcal N}^i_{\Delta ,\sigma }$
-strategy, for the current agitator
${\mathcal N}^i_{\Delta ,\sigma }$
-strategy, for the current agitator
![]() $p_a = p_{a,\sigma }$
and the (oldest)
$p_a = p_{a,\sigma }$
and the (oldest)
![]() $\Lambda $
-axiom putting
$\Lambda $
-axiom putting
![]() $p_a \in \Lambda (A \oplus B)$
with use
$p_a \in \Lambda (A \oplus B)$
with use
![]() $F_a \oplus G_a$
, enumerates the axiom
$F_a \oplus G_a$
, enumerates the axiom
![]() $\langle a,G_a \rangle $
into
$\langle a,G_a \rangle $
into
![]() $\Omega _\sigma $
.
$\Omega _\sigma $
.
If (3) applies, then the
![]() ${\mathcal N}^i_{\Delta ,\sigma }$
-strategy declares a to be confirmed via F, chooses a fresh agitator
${\mathcal N}^i_{\Delta ,\sigma }$
-strategy declares a to be confirmed via F, chooses a fresh agitator
![]() $p_a$
, and enumerates all of
$p_a$
, and enumerates all of
![]() $F - [0,r)$
(for the threshold r imposed on this requirement) into
$F - [0,r)$
(for the threshold r imposed on this requirement) into
![]() $\Phi _i(A)$
with use including all
$\Phi _i(A)$
with use including all
![]() $F_q$
for all agitators
$F_q$
for all agitators
![]() $q \in \overline {K}$
defined by strategies for higher-priority requirements (where
$q \in \overline {K}$
defined by strategies for higher-priority requirements (where
![]() $q \in \Lambda (A \oplus B)$
via an (oldest)
$q \in \Lambda (A \oplus B)$
via an (oldest)
![]() $\Lambda $
-axiom
$\Lambda $
-axiom
![]() $\langle q,F_q \oplus G_q \rangle $
). If now (2) applies to this a, then continue as for that case, else proceed to the global action for this stage.
$\langle q,F_q \oplus G_q \rangle $
). If now (2) applies to this a, then continue as for that case, else proceed to the global action for this stage.
If one of (1)–(3) applies, then we also enumerate into K the agitator q of the
![]() ${\mathcal N}$
-requirement for which we acted at this stage, choose a new fresh agitator q, choose a new threshold r above all numbers mentioned so far which will be imposed on the lower-priority strategies, and initialize all lower-priority
${\mathcal N}$
-requirement for which we acted at this stage, choose a new fresh agitator q, choose a new threshold r above all numbers mentioned so far which will be imposed on the lower-priority strategies, and initialize all lower-priority
![]() ${\mathcal N}$
-strategies.
${\mathcal N}$
-strategies.
If (4) applies, then the
![]() ${\mathcal N}^i_\Delta $
-requirement, i.e., the
${\mathcal N}^i_\Delta $
-requirement, i.e., the
![]() ${\mathcal N}^i_{\Delta ,\sigma }$
-strategies (for all
${\mathcal N}^i_{\Delta ,\sigma }$
-strategies (for all
![]() $\sigma \in 2^r$
, where r is the threshold imposed by the higher-priority strategies) simply defines a new threshold
$\sigma \in 2^r$
, where r is the threshold imposed by the higher-priority strategies) simply defines a new threshold
![]() $r'$
above all numbers mentioned so far which is imposed on all lower-priority
$r'$
above all numbers mentioned so far which is imposed on all lower-priority
![]() ${\mathcal N}$
-strategies.
${\mathcal N}$
-strategies.
After the strategies for an
![]() ${\mathcal N}$
-requirement have acted, the global requirement building
${\mathcal N}$
-requirement have acted, the global requirement building
![]() $\Gamma $
will act. First of all, as we will show in the verification below (see Lemma 2.3), since all corrections will be automatic there will never be a number a and a stage s such that
$\Gamma $
will act. First of all, as we will show in the verification below (see Lemma 2.3), since all corrections will be automatic there will never be a number a and a stage s such that
![]() $a \in \Gamma (B \oplus X_0 \oplus X_1) - A$
. So the global requirement will simply identify the (oldest)
$a \in \Gamma (B \oplus X_0 \oplus X_1) - A$
. So the global requirement will simply identify the (oldest)
![]() $a \in A - \Gamma (B \oplus X_0 \oplus X_1)$
(which must exist since A is infinite), let Q be the set of all current agitators q of
$a \in A - \Gamma (B \oplus X_0 \oplus X_1)$
(which must exist since A is infinite), let Q be the set of all current agitators q of
![]() ${\mathcal N}$
-requirements whose current threshold r is less than
${\mathcal N}$
-requirements whose current threshold r is less than
![]() $<a$
, and then enumerate an axiom
$<a$
, and then enumerate an axiom
![]() $\langle a, B_a \oplus C^0_a \oplus C^1_a \rangle $
into
$\langle a, B_a \oplus C^0_a \oplus C^1_a \rangle $
into
![]() $\Gamma $
where:
$\Gamma $
where:
-
•
 $B_a$
contains all sets
$B_a$
contains all sets
 $G_q$
such that
$G_q$
such that
 $q \in \Lambda (A \oplus B)$
via a
$q \in \Lambda (A \oplus B)$
via a
 $\Lambda $
-axiom
$\Lambda $
-axiom
 $\langle q, F_q \oplus G_q \rangle $
for some
$\langle q, F_q \oplus G_q \rangle $
for some
 $q \in Q$
and some finite set
$q \in Q$
and some finite set
 $F_q$
,
$F_q$
, -
•
 $C^0_a$
contains all
$C^0_a$
contains all
 $c^0_{a'}$
for all
$c^0_{a'}$
for all
 $a' \in F_q$
such that
$a' \in F_q$
such that
 $q \in \Lambda (A \oplus B)$
via a
$q \in \Lambda (A \oplus B)$
via a
 $\Lambda $
-axiom
$\Lambda $
-axiom
 $\langle q, F_q \oplus G_q \rangle $
for some
$\langle q, F_q \oplus G_q \rangle $
for some
 $q \in Q$
and some finite sets
$q \in Q$
and some finite sets
 $F_q$
and
$F_q$
and
 $G_q$
, as well as a freshly chosen number
$G_q$
, as well as a freshly chosen number
 $c^0_a$
for which we enumerate
$c^0_a$
for which we enumerate
 $c^0_a$
into
$c^0_a$
into
 $X_0$
via a
$X_0$
via a
 $\Phi _0$
-axiom
$\Phi _0$
-axiom
 $\langle c^0_a,\{a\} \rangle $
, and
$\langle c^0_a,\{a\} \rangle $
, and -
•
 $C^1_a$
contains all
$C^1_a$
contains all
 $c^1_{a'}$
for all
$c^1_{a'}$
for all
 $a' \in F_q$
such that
$a' \in F_q$
such that
 $q \in \Lambda (A \oplus B)$
via a
$q \in \Lambda (A \oplus B)$
via a
 $\Lambda $
-axiom
$\Lambda $
-axiom
 $\langle q, F_q \oplus G_q \rangle $
for some
$\langle q, F_q \oplus G_q \rangle $
for some
 $q \in Q$
and some finite sets
$q \in Q$
and some finite sets
 $F_q$
and
$F_q$
and
 $G_q$
, as well as a freshly chosen number
$G_q$
, as well as a freshly chosen number
 $c^1_a$
for which we enumerate
$c^1_a$
for which we enumerate
 $c^1_a$
into
$c^1_a$
into
 $X_1$
via a
$X_1$
via a
 $\Phi _1$
-axiom
$\Phi _1$
-axiom
 $\langle c^1_a,\{a\} \rangle $
.
$\langle c^1_a,\{a\} \rangle $
.
In the last two bullets above, for each
![]() $a'$
, if there is no
$a'$
, if there is no
![]() $c^i_{a'}$
(for
$c^i_{a'}$
(for
![]() $i<2$
) which has not yet been dumped and for which there is a
$i<2$
) which has not yet been dumped and for which there is a
![]() $\Phi _i$
-axiom
$\Phi _i$
-axiom
![]() $\langle c^i_{a'},\{a'\} \rangle $
, then we pick a fresh such number
$\langle c^i_{a'},\{a'\} \rangle $
, then we pick a fresh such number
![]() $c^i_{a'}$
for the
$c^i_{a'}$
for the
![]() $\Gamma $
-axiom, enumerate a corresponding axiom
$\Gamma $
-axiom, enumerate a corresponding axiom
![]() $\langle c^i_{a'},\{a'\} \rangle $
into
$\langle c^i_{a'},\{a'\} \rangle $
into
![]() $\Phi _i$
, and use it in the above
$\Phi _i$
, and use it in the above
![]() $\Gamma $
-axiom. Also, recall here that each current agitator
$\Gamma $
-axiom. Also, recall here that each current agitator
![]() $q \in Q$
must be in
$q \in Q$
must be in
![]() $\overline {K}$
and thus in
$\overline {K}$
and thus in
![]() $\Lambda (A \oplus B)$
.
$\Lambda (A \oplus B)$
.
This concludes the formal description of the construction.
2.5 Verification
We now verify that our construction satisfies the requirements in a number of lemmas. In addition to assuming that
![]() $\overline {K} = \Lambda (A \oplus B)$
and that
$\overline {K} = \Lambda (A \oplus B)$
and that
![]() $A \oplus B$
has a good approximation, we will also assume tacitly throughout that
$A \oplus B$
has a good approximation, we will also assume tacitly throughout that
![]() $A \not \le _e B$
and in particular that A is infinite.
$A \not \le _e B$
and in particular that A is infinite.
We start by verifying that our construction is indeed finite injury:
Lemma 2.1. Each
![]() ${\mathcal N}$
-requirement acts at most finitely often and eventually defines a final threshold r and a final agitator q which is in
${\mathcal N}$
-requirement acts at most finitely often and eventually defines a final threshold r and a final agitator q which is in
![]() $\overline {K} ($
unless it does not have an eventual agitator at all
$\overline {K} ($
unless it does not have an eventual agitator at all
![]() $)$
.
$)$
.
Proof We proceed by induction on the priority of the
![]() ${\mathcal N}$
-requirement. So fix an
${\mathcal N}$
-requirement. So fix an
![]() ${\mathcal N}^i_\Delta $
-requirement and assume the lemma for all higher-priority
${\mathcal N}^i_\Delta $
-requirement and assume the lemma for all higher-priority
![]() ${\mathcal N}$
-requirements. Fix a (least) stage
${\mathcal N}$
-requirements. Fix a (least) stage
![]() $s_0$
such that no higher-priority
$s_0$
such that no higher-priority
![]() ${\mathcal N}$
-requirement acts after stage
${\mathcal N}$
-requirement acts after stage
![]() $s_0$
. Let
$s_0$
. Let
![]() $r_0$
be the maximum of the final thresholds of all these higher-priority
$r_0$
be the maximum of the final thresholds of all these higher-priority
![]() ${\mathcal N}$
-requirements, and let Q be the set of the final agitators of all these higher-priority
${\mathcal N}$
-requirements, and let Q be the set of the final agitators of all these higher-priority
![]() ${\mathcal N}$
-requirements.
${\mathcal N}$
-requirements.
Let’s now analyze how the
![]() ${\mathcal N}^i_\Delta $
-requirement can require attention after stage
${\mathcal N}^i_\Delta $
-requirement can require attention after stage
![]() $s_0$
: First of all, observe that clause (4) of the third bullet can apply at most once after stage
$s_0$
: First of all, observe that clause (4) of the third bullet can apply at most once after stage
![]() $s_0$
.
$s_0$
.
For the sake of a contradiction, assume that an
![]() ${\mathcal N}^i_{\Delta ,\sigma }$
-strategy acts infinitely often. By the first bullet in the conditions for requiring attention, there can be no
${\mathcal N}^i_{\Delta ,\sigma }$
-strategy acts infinitely often. By the first bullet in the conditions for requiring attention, there can be no
![]() $a \in A$
with
$a \in A$
with
![]() $\sigma (a)=0$
.
$\sigma (a)=0$
.
Furthermore, clause (3) of the third bullet must apply infinitely often (and thus infinitely many a will be confirmed by the
![]() ${\mathcal N}^i_{\Delta ,\sigma }$
-strategy), since clauses (1) and (2) of the third bullet can possibly apply to a fixed a only if
${\mathcal N}^i_{\Delta ,\sigma }$
-strategy), since clauses (1) and (2) of the third bullet can possibly apply to a fixed a only if
![]() $a \notin A$
, but then the age of a keeps increasing and, since A is infinite, infinitely many other numbers must take precedence in requiring attention. This implies, by age and clause (3) of the third bullet, that each
$a \notin A$
, but then the age of a keeps increasing and, since A is infinite, infinitely many other numbers must take precedence in requiring attention. This implies, by age and clause (3) of the third bullet, that each
![]() $a \in A$
must eventually be confirmed, and so, since the first bullet fails for
$a \in A$
must eventually be confirmed, and so, since the first bullet fails for
![]() $\sigma $
,
$\sigma $
,
![]() $a \in \Delta (X_i)$
. But then there will be a final agitator
$a \in \Delta (X_i)$
. But then there will be a final agitator
![]() $p_a = p_{a,\sigma }$
, which will be in
$p_a = p_{a,\sigma }$
, which will be in
![]() $\overline {K}$
and thus in
$\overline {K}$
and thus in
![]() $\Lambda (A \oplus B)$
via a
$\Lambda (A \oplus B)$
via a
![]() $\Lambda $
-axiom
$\Lambda $
-axiom
![]() $\langle p_a, F_a \oplus G_a \rangle $
, say. Thus
$\langle p_a, F_a \oplus G_a \rangle $
, say. Thus
![]() $a \in \Omega _\sigma (B)$
via the axiom
$a \in \Omega _\sigma (B)$
via the axiom
![]() $\langle a,G_a \rangle $
. Conversely, if
$\langle a,G_a \rangle $
. Conversely, if
![]() $a \notin A$
, then any axiom
$a \notin A$
, then any axiom
![]() $\langle a,G_a \rangle $
enumerated into
$\langle a,G_a \rangle $
enumerated into
![]() $\Omega _\sigma $
cannot apply and put
$\Omega _\sigma $
cannot apply and put
![]() $a \in \Omega _\sigma (B)$
since otherwise,
$a \in \Omega _\sigma (B)$
since otherwise,
![]() $G_a \subseteq B$
while the corresponding agitator
$G_a \subseteq B$
while the corresponding agitator
![]() $p_a \notin \overline {K}$
, so the second bullet for requiring attention will eventually prevent any
$p_a \notin \overline {K}$
, so the second bullet for requiring attention will eventually prevent any
![]() ${\mathcal N}^i_\Delta $
-strategy from acting. We have thus shown that an
${\mathcal N}^i_\Delta $
-strategy from acting. We have thus shown that an
![]() ${\mathcal N}^i_{\Delta ,\sigma }$
-strategy acting infinitely often will imply
${\mathcal N}^i_{\Delta ,\sigma }$
-strategy acting infinitely often will imply
![]() $A = \Omega _\sigma (B)$
, contrary to assumption.
$A = \Omega _\sigma (B)$
, contrary to assumption.
Thus the
![]() ${\mathcal N}^i_\Delta $
-requirement will act at most finitely often and eventually define a final threshold r and a final agitator q (if there is an agitator q ever defined).
${\mathcal N}^i_\Delta $
-requirement will act at most finitely often and eventually define a final threshold r and a final agitator q (if there is an agitator q ever defined).
Note that the action of the global requirement does not interfere with any of the above argument.
We next verify that each
![]() ${\mathcal N}$
-requirement is satisfied.
${\mathcal N}$
-requirement is satisfied.
Lemma 2.2. Each
![]() ${\mathcal N}^i_\Delta $
-requirement is satisfied.
${\mathcal N}^i_\Delta $
-requirement is satisfied.
Proof Suppose that
![]() $A = \Delta (X_i)$
. Fix the final threshold r of the higher-priority
$A = \Delta (X_i)$
. Fix the final threshold r of the higher-priority
![]() ${\mathcal N}$
-requirements and set
${\mathcal N}$
-requirements and set
![]() $\sigma = A {\,\upharpoonright \,} r$
. We will show that the
$\sigma = A {\,\upharpoonright \,} r$
. We will show that the
![]() ${\mathcal N}^i_{\Delta ,\sigma }$
-strategy acts infinitely often, contradicting Lemma 2.1.
${\mathcal N}^i_{\Delta ,\sigma }$
-strategy acts infinitely often, contradicting Lemma 2.1.
First, note that for each a, the first and second bullets of requiring attention will eventually not prevent the
![]() ${\mathcal N}^i_{\Delta ,\sigma }$
-strategy from acting. (This is clear for the first bullet by definition of
${\mathcal N}^i_{\Delta ,\sigma }$
-strategy from acting. (This is clear for the first bullet by definition of
![]() $\sigma $
, and for the second bullet, we argue that otherwise,
$\sigma $
, and for the second bullet, we argue that otherwise,
![]() $p_a \in K$
and
$p_a \in K$
and
![]() $G_a \subseteq B$
implies
$G_a \subseteq B$
implies
![]() $p_a \notin \Lambda (A \oplus B)$
and so
$p_a \notin \Lambda (A \oplus B)$
and so
![]() $F_a \not \subseteq A$
, say,
$F_a \not \subseteq A$
, say,
![]() $a' \in F_a - A$
. But
$a' \in F_a - A$
. But
![]() $a'$
is confirmed, so
$a'$
is confirmed, so
![]() $ \in \Delta (X_i) - A$
, contradicting our assumption.)
$ \in \Delta (X_i) - A$
, contradicting our assumption.)
But now
![]() $A = \Delta (X_i)$
implies that every
$A = \Delta (X_i)$
implies that every
![]() $a \in A$
will be confirmed, implying that the
$a \in A$
will be confirmed, implying that the
![]() ${\mathcal N}^i_{\Delta ,\sigma }$
-strategy acts infinitely often, again contradicting Lemma 2.1.
${\mathcal N}^i_{\Delta ,\sigma }$
-strategy acts infinitely often, again contradicting Lemma 2.1.
Finally, we need to verify that the global requirement is satisfied.
Lemma 2.3. The global requirement is satisfied:
![]() $A = \Gamma (B \oplus X_0 \oplus X_1)$
.
$A = \Gamma (B \oplus X_0 \oplus X_1)$
.
Proof We need to prove two directions. Assume first that
![]() $a \in A$
, so we need to verify that some
$a \in A$
, so we need to verify that some
![]() $\Gamma $
-axiom will eventually put a into
$\Gamma $
-axiom will eventually put a into
![]() $\Gamma (B \oplus X_0 \oplus X_1)$
. So find a stage s such that all thresholds r of
$\Gamma (B \oplus X_0 \oplus X_1)$
. So find a stage s such that all thresholds r of
![]() ${\mathcal N}$
-requirements with
${\mathcal N}$
-requirements with
![]() $r<a$
, as well as their potential agitators q, have settled down. Then for each such agitator q,
$r<a$
, as well as their potential agitators q, have settled down. Then for each such agitator q,
![]() $q \in \overline {K}$
and thus there will be a stable
$q \in \overline {K}$
and thus there will be a stable
![]() $\Lambda $
-axiom
$\Lambda $
-axiom
![]() $\langle q, F_q \oplus G_q \rangle $
putting
$\langle q, F_q \oplus G_q \rangle $
putting
![]() $q \in \Lambda (A \oplus B)$
, say, all of this happens by a stage
$q \in \Lambda (A \oplus B)$
, say, all of this happens by a stage
![]() $s' \ge s$
. Then by stage
$s' \ge s$
. Then by stage
![]() $s'$
, the global strategy will have enumerated a
$s'$
, the global strategy will have enumerated a
![]() $\Gamma $
-axiom
$\Gamma $
-axiom
![]() $\langle a, B_a \oplus C^0_a \oplus C^1_a \rangle $
with
$\langle a, B_a \oplus C^0_a \oplus C^1_a \rangle $
with
![]() $B_a \subseteq B$
and
$B_a \subseteq B$
and
![]() $C^i_a \subseteq X_i$
for
$C^i_a \subseteq X_i$
for
![]() $i<2$
, and so
$i<2$
, and so
![]() $a \in \Gamma (B \oplus X_0 \oplus X_1)$
.
$a \in \Gamma (B \oplus X_0 \oplus X_1)$
.
Conversely, suppose
![]() $a \notin A$
, so we need to show that no valid
$a \notin A$
, so we need to show that no valid
![]() $\Gamma $
-axiom puts a into
$\Gamma $
-axiom puts a into
![]() $\Gamma (B \oplus X_0 \oplus X_1)$
. For the sake of a contradiction, suppose that at some stage s, while
$\Gamma (B \oplus X_0 \oplus X_1)$
. For the sake of a contradiction, suppose that at some stage s, while
![]() $a \in A_s$
, the global strategy enumerates a valid axiom
$a \in A_s$
, the global strategy enumerates a valid axiom
![]() $\langle a, B_a \oplus C^0_a \oplus C^1_a \rangle $
into
$\langle a, B_a \oplus C^0_a \oplus C^1_a \rangle $
into
![]() $\Gamma $
. We now distinguish two possibilities:
$\Gamma $
. We now distinguish two possibilities:
Assume first that after this stage s, no
![]() ${\mathcal N}$
-requirement with current threshold
${\mathcal N}$
-requirement with current threshold
![]() $r \le a$
acts; then the
$r \le a$
acts; then the
![]() ${\mathcal N}$
-requirements with threshold
${\mathcal N}$
-requirements with threshold
![]() $r \le a$
cannot dump any numbers
$r \le a$
cannot dump any numbers
![]() $c^i_{a'}$
into
$c^i_{a'}$
into
![]() $X_i$
involved in the
$X_i$
involved in the
![]() $\Gamma $
-axiom putting a into
$\Gamma $
-axiom putting a into
![]() $\Gamma (B \oplus X_0 \oplus X_1)$
(for either
$\Gamma (B \oplus X_0 \oplus X_1)$
(for either
![]() $i<2$
); and only the highest-priority
$i<2$
); and only the highest-priority
![]() ${\mathcal N}$
-requirement with threshold
${\mathcal N}$
-requirement with threshold
![]() $r>a$
can dump any such numbers into only one of the
$r>a$
can dump any such numbers into only one of the
![]() $X_i$
, so
$X_i$
, so
![]() $a \notin \Gamma (B \oplus X_0 \oplus X_1)$
by an
$a \notin \Gamma (B \oplus X_0 \oplus X_1)$
by an
![]() $X_{1-i}$
-change.
$X_{1-i}$
-change.
On the other hand, suppose that some
![]() ${\mathcal N}$
-requirement with current threshold
${\mathcal N}$
-requirement with current threshold
![]() $r \le a$
acts, say, the first such requirement is an
$r \le a$
acts, say, the first such requirement is an
![]() ${\mathcal N}^j$
-requirement acting at a stage
${\mathcal N}^j$
-requirement acting at a stage
![]() $s'>s$
. In that case, the
$s'>s$
. In that case, the
![]() ${\mathcal N}^j$
-requirement’s current agitator q will be enumerated into K, and so the
${\mathcal N}^j$
-requirement’s current agitator q will be enumerated into K, and so the
![]() $\Lambda $
-axiom involving
$\Lambda $
-axiom involving
![]() $F_q \oplus G_q$
will no longer apply. Now if
$F_q \oplus G_q$
will no longer apply. Now if
![]() $G_q \not \subseteq B$
, then the
$G_q \not \subseteq B$
, then the
![]() $\Gamma $
-axiom will clearly no longer apply for a. If only
$\Gamma $
-axiom will clearly no longer apply for a. If only
![]() $F_q \not \subseteq A$
, then we will need to argue that
$F_q \not \subseteq A$
, then we will need to argue that
![]() $C^0_a \not \subseteq X_0$
or
$C^0_a \not \subseteq X_0$
or
![]() $C^1_a \not \subseteq X_1$
to invalidate the
$C^1_a \not \subseteq X_1$
to invalidate the
![]() $\Gamma $
-axiom for a, but by the choice of the numbers
$\Gamma $
-axiom for a, but by the choice of the numbers
![]() $c^i_{a'}$
in the definition of the
$c^i_{a'}$
in the definition of the
![]() $\Gamma $
-axiom for a, both
$\Gamma $
-axiom for a, both
![]() $c^0_{a'}$
and
$c^0_{a'}$
and
![]() $c^1_{a'}$
will leave
$c^1_{a'}$
will leave
![]() $X_0$
and
$X_0$
and
![]() $X_1$
, respectively, unless they will be dumped. However, since any
$X_1$
, respectively, unless they will be dumped. However, since any
![]() ${\mathcal N}$
-requirement of lower priority than the
${\mathcal N}$
-requirement of lower priority than the
![]() ${\mathcal N}^j$
-requirement is prevented from dumping a number in
${\mathcal N}^j$
-requirement is prevented from dumping a number in
![]() $C^{1-j}_a$
into
$C^{1-j}_a$
into
![]() $X_{1-j}$
after the
$X_{1-j}$
after the
![]() ${\mathcal N}^j$
-requirement acts at stage
${\mathcal N}^j$
-requirement acts at stage
![]() $s'$
, we know that
$s'$
, we know that
![]() $C^{1-j}_a \not \subseteq X_{1-j}$
as long as no
$C^{1-j}_a \not \subseteq X_{1-j}$
as long as no
![]() ${\mathcal N}$
-requirement of higher priority acts later. If that should happen, we repeat the above argument until there is no even higher-priority
${\mathcal N}$
-requirement of higher priority acts later. If that should happen, we repeat the above argument until there is no even higher-priority
![]() ${\mathcal N}$
-requirement acting to dump even smaller numbers. So eventually, we see that this
${\mathcal N}$
-requirement acting to dump even smaller numbers. So eventually, we see that this
![]() $\Gamma $
-axiom cannot apply to a anymore, as desired.
$\Gamma $
-axiom cannot apply to a anymore, as desired.
This establishes that the global requirement does indeed succeed as desired, completing the proof.
Funding
The first author’s research was partially supported by development program of Volga Region Mathematical Center (agreement no. 075-02-2022-882). The second author’s research was partially supported by NSF Binational grant DMS-DMS-1101123 entitled “Collaboration in Computability” and AMS-Simons Foundation Collaboration Grant 209087. The third author’s research was partially supported by the Ministry of Education, Singapore, under its Academic Research Fund Tier 1 (RG23/19). The fourth author’s research was partially supported by the Russian Science Foundation (project no. 22-21-20024; https://rscf.ru/project/22-21-20024/). This research was partially carried out while the second and third authors were visiting Kazan Federal University.