Published online by Cambridge University Press: 12 March 2014
In [10, §0, E), 5)] Shelah states using the proofs of 7.9 and 6.9 in [9] it is possible to prove that if a countable first-order theory T is ℵ0-stable (totally transcendental) and not ℵ1-categorical, then it has at least ∣1 + α∣ models of power ℵα.
In this note we will give a new proof of this theorem using the work of Baldwin and Lachlan [1]. Our original proof used the generalized continuum hypothesis (GCH). We are indebted to G. E. Sacks for suggesting that the notions of ℵ0-stability and ℵ1-categoricity are absolute, and that consequently our use of GCH was eliminable [8]. Routine results from model theory may be found, e.g. in [2].
Proof (with GCH). In the proof of Theorem 3 of [1] Baldwin and Lachlin show 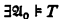 of power ℵα such that there is a countable definable subset in
of power ℵα such that there is a countable definable subset in 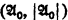 . Let B0 be such a subset. Say
. Let B0 be such a subset. Say 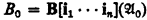 . We will give by transfinite induction an elementary chain
. We will give by transfinite induction an elementary chain 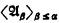 of models of T of power ℵα such that B[i1 … in]
of models of T of power ℵα such that B[i1 … in]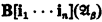 has power ℵβ and such that every infinite definable subset of
has power ℵβ and such that every infinite definable subset of 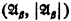 has power ≥ℵβ. This clearly suffices.
has power ≥ℵβ. This clearly suffices.