Published online by Cambridge University Press: 12 March 2014
In the first of her papers on functional calculi based on strict implication, Ruth Barcan Marcus takes as her starting point the Lewis systems S2 and S4, supplemented by one of the normal bases for quantification theory, and by one special axiom for the mixture, asserting that if possibly something φ's then something possibly φ's. In the symbolism of Łukasiewicz, which will be used here, this axiom is expressible as CMΣxφxΣxMφx. In the present note I propose to show that if S5 had been taken as a startingpoint rather than S2 or S4, this formula need not have been laid down as an axiom but could have been deduced as a theorem.
It has been shown by Gödel that a system equivalent to S5 may be obtained if we add to any complete basis for the classical propositional calculus a pair of symbols for ‘Necessarily’ and ‘Possibly,’ which here will be ‘L’ and ‘M’; the axioms
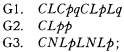
the rule
RL: If α is a thesis, so is Lα;
and the definition
Df. M: M = NLN.
1 Barcan, Ruth C., A functional calculus of first order based on strict implication, this Journal, vol. 11 (1946), p. 2Google Scholar, Proposition 11.
2 Gödel, K., Eine Interpretation des intuitionistischen Aussagenkalküls, Ergebnisse eines mathematischen Kolloquiums, Heft 4 (1933), pp. 39–41Google Scholar, cited in Feys, R., Les systemes formalisés des modalités aristotéliciennes, Revue philosophique de Louvain, 11. 1950, 16.1–16.24Google Scholar.
3 Łukasiewicz, J., Aristotle's syllogistic (Oxford, 1951), §§ 19, 24Google Scholar.