Mixed systems

Extract

In [A₁]–[A₄] there is an abstract description, in terms of “α-systems”, of the object of a nested priority construction, and there is a metatheorem listing conditions which guarantee the success of the construction. The metatheorem has different versions, with later versions becoming simpler and more general. The information needed to meet the requirements is enumerated by a 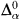function, where α is an arbitrary recursive ordinal. All other objects associated with the α-system are r.e. In the basic metatheorem, the requirements must all be at level α, although there is a special result, for limit α, which allows one requirement at each level in an increasing sequence with limit α. There are other abstract descriptions of nested priority arguments in [K₁], [K₂], [K₃], and [L-L].

A typical use of α-systems is that in [B], where it is shown that, for a relation R on a recursive structure 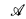, under suitable assumptions, if R does not have a “recursive Σ_α” definition in 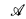, then there is a recursive isomorphic copy of 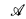in which the image of R is not . There is no difficulty in generalizing this to make each of infinitely many relations not , when the assumptions are uniformly satisfied and each relation has no recursive Σ_α definition. However, the metatheorems for α-systems do not apply to the situation where we have several (even two) relations R_i, which do not have recursive Σ_βi definitions and whose images we wish to make not 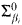for distinct β_i. An even more basic problem is to construct a recursive copy of a recursive structure via an isomorphism whose restriction to various sets U_i, is not 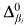If β_i, = α for all i, then we can use an (α + 1)-system; otherwise, the old metatheorems do not apply.