Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-12-02T19:46:49.176Z Has data issue: false hasContentIssue false
  • English
  • Français

The McKinsey axiom is not compact

Published online by Cambridge University Press:  12 March 2014

Xiaoping Wang
Xiaoping Wang*
Affiliation:
Philosophy Department, Tulane University
Get access Rights & Permissions [Opens in a new window]

Extract

The canonicity and compactness of the KM system are problems historically important in the development of our understanding of intensional logic (as explained in Goldblatt's paper, The McKinsey axiom is not canonical). The problems, however, were unsolved for years in modal logic. In the beginning of 1990, Goldblatt showed that KM is not canonical in The McKinsey axiom is not canonical. The remaining task is to solve the problem of the compactness of KM. In this paper we present a proof showing that the KM system is not compact.

The symbols of the language of propositional modal logic are as follows:

1. A denumerably infinite set of sentence letters, for example, {p0, P1, p2, …};

2. The Boolean connectives &, ⋁, ¬, →, ↔ and parentheses;

3. The modal operators L and M where M is defined as ¬L¬.

The formation rules of well-formed propositional modal formulae are the formation rules of formulae in classic propositional logic plus the following rule:

If A is a well-formed formula, so is LA.

A normal modal system is a set of formulae that contains all tautologies and the formula

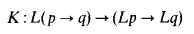
and is closed under the following transformation rules:

Uniform substitution. If A is a theorem, so is every substitution-instance of A.

Modus ponens. If A and A → B are theorems, so is B.

Necessitation. If A is a theorem, so is LA.

Let L be a normal system. Then a set S of formulae is L-consistent if and only if for any formula B, which is the conjunction of some formulae in S, B is not included in L. A set S of formulae is maximal if and only if for every formula A, S either contains A or contains ¬A. A set S of formulae is maximal L-consistent if and only if it is both maximal and L-consistent.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 57 , Issue 4 , December 1992 , pp. 1230 - 1238
Copyright
Copyright © Association for Symbolic Logic 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

van Benthem, J. F. A. K. [1980], Some kinds of modal completeness, Stadia Logica, vol. 39, pp. 129–141.Google Scholar
Fine, K. [1974], An incomplete logic containing S4, Theoria, vol. 40, pp. 23–29.CrossRefGoogle Scholar
Goldblatt, R. I. [1975], First-order definability in modal logic, this Journal, vol. 40, pp. 35–40.Google Scholar
Goldblatt, R. I. [1990], The McKinsey axiom is not canonical, this Journal, vol. 56, pp. 554–562.Google Scholar
Hughes, G. E. and Cresswell, M. J. [1968], An introduction to modal logic, Methuen, London.Google Scholar
Goldblatt, R. I. [1984], A companion to modal logic, Methuen, London.Google Scholar
Segerberg, K. [1972], Post completeness in modal logic, this Journal, vol. 37, pp. 711–715.Google Scholar
Thomason, S. K. [1974], An incompleteness theorem in modal logic, Theoria, vol. 40, pp. 30–34.CrossRefGoogle Scholar