Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-25T08:10:48.408Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalised weak presentations

Published online by Cambridge University Press:  12 March 2014

Alexandra Shlapentokh
Alexandra Shlapentokh*
Affiliation:
East Carolina University, Department of Mathematics, Greenville, NC 27858., USA, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let K be a computable field. Let ℱ be a collection of recursive functions over K, possibly including field operations. We investigate the following question. Given an r.e. degree 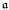. is there an injective map j : K → ℕ such that j(K) is of degree a and all the functions in ℱ are translated by restrictions of total recursive functions.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 67 , Issue 2 , June 2002 , pp. 787 - 819
Copyright
Copyright © Association for Symbolic Logic 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Artin, E., Algebraic Numbers and Algebraic Functions, Gordon Breach Science Publishers, New York, 1986.Google Scholar
[2]Ash, C. J. and Knight, J. F., Possible degrees in recursive copies, Annals of Pure and Applied Logic, vol. 75 (1995), no. 3, pp. 215–221.CrossRefGoogle Scholar
[3]Ash, C. J., Possible degrees in rucursive copies, II, Annals of Pure and Applied Logic, vol. 87 (1997), no. 2, pp. 151–165.CrossRefGoogle Scholar
[4]Ash, C. J., Knight, J. F., and Remmel, J. B., Quasi-simple relations in copies of a given recursive structure, Annals of Pure and Applied Logic, vol. 86, no. 3, pp. 203–218.CrossRefGoogle Scholar
[5]Baker, A., Transcendental Number Theory, Cambridge Mathematical Library, Cambridge University Press, Cambridge, 1990.Google Scholar
[6]Chevalley, C., Introduction to the theory of algebraic functions of one variable, Mathematical Surveys, vol. 6, AMS, Providence, RI, 1951.CrossRefGoogle Scholar
[7]Fried, M. and Jarden, M., Field Arithmetic, Springer Verlag, New York, 1986.CrossRefGoogle Scholar
[8]Harizanov, V., Some effects of Ash-Nerode and other decidability conditions on degree spectra, Annals of Pure and Applied Logic, vol. 55 (1991), pp. 51–65.CrossRefGoogle Scholar
[9]Harizanov, V., Uncountable degree spectra, Annals of Pure and Applied Logic, vol. 54 (1991), pp. 255–263.CrossRefGoogle Scholar
[10]Harizanov, V., The possible Turing degree of the nonzero member in a two element degree spectrum, Annals of Pure and Applied Logic, vol. 60 (1993), pp. 1–30.CrossRefGoogle Scholar
[11]Januz, G., Algebraic Number Fields, Academic Press, New York, 1973.Google Scholar
[12]Jockusch, C. and Shlapentokh, A., Weak presentations of computable fields, this Journal, vol. 60 (1995), pp. 199–208.Google Scholar
[13]Rabin, M., Computable algebra, Transactions of the American Mathematical Society, vol. 95 (1960), pp. 341–360.Google Scholar
[14]Shlapentokh, A., Diophantine equivalence and countable rings, this Journal, vol. 59 (1994), pp. 1068–1095.Google Scholar
[15]Shlapentokh, A., Non-standard extensions of weak presentations, Journal of Algebra, vol. 176 (1995), pp. 735–749.CrossRefGoogle Scholar
[16]Shlapentokh, A., Algebraic and Turing separability of rings, Journal of Algebra, vol. 185 (1996), pp. 229–257.CrossRefGoogle Scholar
[17]Shlapentokh, A., Rational separability over global fields, Annals of Pure and Applied Logic, vol. 79 (1996), pp. 93–108.CrossRefGoogle Scholar
[18]Shlapentokh, A., The logic ofpseudo S-integers, Israel Journal of Mathematics, vol. 101 (1997), pp. 229–254.CrossRefGoogle Scholar
[19]Shlapentokh, A., Weak presentations of fields not extendible to recursive presentations, Recursion Theory and Complexity, Proceedings of the International Workshop on Complexity and Computability, 1997, pp. 131–155.Google Scholar
[20]Shlapentokh, A., Weak presentations of non-finitely generated fields, Annals of Pure and Applied Logic, vol. 28 (1998), pp. 223–252.CrossRefGoogle Scholar