Article contents
The existence of countable totally nonconstructive extensions of the countable atomless Boolean algebra
Published online by Cambridge University Press: 12 March 2014
Abstract
Our results concern the existence of a countable extension 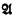 of the countable atomless Boolean algebra
of the countable atomless Boolean algebra 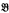 such that
such that 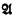 is a “nonconstructive” extension of
is a “nonconstructive” extension of 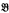 . It is known that for any fixed admissible indexing φ of
. It is known that for any fixed admissible indexing φ of 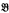 there is a countable nonconstructive extension
there is a countable nonconstructive extension 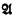 of
of 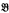 (relative to φ). The main theorem here shows that there exists an extension
(relative to φ). The main theorem here shows that there exists an extension 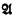 of
of 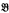 such that for any admissible indexing φ of
such that for any admissible indexing φ of 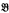 ,
, 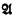 is nonconstructive (relative to φ).Thus, in this sense
is nonconstructive (relative to φ).Thus, in this sense 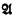 a countable totally nonconstructive extension of
a countable totally nonconstructive extension of 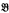 .
.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1983
References
REFERENCES
- 2
- Cited by


