Published online by Cambridge University Press: 12 March 2014
Some syntactically simple fragments of intuitionistic logic possess considerable expressive power compared with their classical counterparts.
In particular, we consider in this paper intuitionistic second order propositional logic (ISPL) a formalisation of which may be obtained by adding to the intuitionistic propositional calculus quantifiers binding propositional variables together with the usual quantifier rules and the axiom scheme (Ex)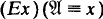 , where
, where 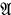 is a formula not containing x.
is a formula not containing x.
The main purpose of this paper is to show that the classical first order predicate calculus with identity can be (isomorphically) embedded in ISPL.
It turns out an immediate consequence of this that the classical first order predicate calculus with identity can also be embedded in the fragment (PLA) of the intuitionistic first order predicate calculus whose only logical symbols are → and (.) (universal quantifier) and the only nonlogical symbol (apart from individual variables and parentheses) a single monadic predicate letter.
Another consequence is that the classical first order predicate calculus can be embedded in the theory of Heyting algebras.
The undecidability of the formal systems under consideration evidently follows immediately from the present results.
We shall indicate how the methods employed may be extended to show also that the intuitionistic first order predicate calculus with identity can be embedded in both ISPL and PLA.
For the purpose of the present paper it will be convenient to use the following formalisation (S) of ISPL based on [3], rather than the one given above.