Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-18T23:54:04.588Z Has data issue: false hasContentIssue false
  • English
  • Français

Élimination des quantificateurs dans des paires de corps

Published online by Cambridge University Press:  12 March 2014

G. Leloup
G. Leloup*
Affiliation:
Département de Mathématiques, Université de Limoges, 87060 Limoges, France
Get access Rights & Permissions [Opens in a new window]

Extract

On sait que par le choix d’ un langage suffisamment complexe, toute structure peut admettre une élimination des quantificateurs, malheureusement cette extension du langage peut nous éloigner des phénomènes algébriques. Nous allons nous intéresser à l’ élimination des quantificateurs pour des paires de corps. Dans le cas des paires de corps algébriquement clos et des paires denses de corps réel clos, on obtient une élimination en ajoutant au langage des prédicats ayant une signification algébrique: on peut les exprimer en disant que pour deux ensembles algébriques 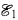et 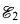donnés, il existe des points du sous-corps rationnels pour 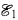et pas pour 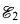, ou qu’ un ensemble semi-algébrique donné a des points rationnels sur le sous-corps. Robinson avait déjà abordé de façon informelle le cas des paires denses de corps réel-clos (cf. [Ro 2, p. 198]). Partant du langage des paires de corps ordonnés, enrichi de symboles de relations correspondant à l’ indépendance algébrique, il proposait d’ ajouter pas à pas des fonctions de Skolem Herbrand pour faire disparaitre les quantificateurs existentiels des formules, mais sans préciser le langage obtenu. Ici nous approchons le problème différemment en explicitant dès le départ le langage utilisé.

Grâce à ces résultats nous pourrons étudier le cas des paires séparées de corps réels clos ainsi que des paires de corps valués henseliens. En élargissant la définition d’ ensemble algébrique à tous les symboles du langage, les prédicats relationnels ajoutés ont la même signification que dans le cas des paires de corps algébriquement clos.

En comparant les techniques employées ici avec celles déjà utilisées dans [K], [B], [D 1] et [L], on remarque qu’il est possible de traîter une grande partie de l’ étude (complétude, modèle complétude, élimination des quantificateurs) des paires de corps algébriquement clos, réel-clos ou henseliens en se basant sur des prolongements d’ isomorphismes entre sous-structures dénombrables où l’ une des deux est contenue dans une structure ω1-saturée.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 60 , Issue 2 , June 1995 , pp. 548 - 562
Copyright
Copyright © Association for Symbolic Logic 1995

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

RÉFÉRENCES

[Ba] Baur, W., Die Theorie der Paare reell abgeschlossener Körper, Logic and Algorithmic (in honour of E. Specker), Monographies de l’Enseignement Mathématique, no. 30, Université de Geneve, Genèva, 1982, pp. 25–34.Google Scholar
[B] Baur, W., On the theory of pairs of real closed fields, this Journal, vol. 47 (1982), pp. 669–679.Google Scholar
[C-K] Chang, C. C. and Keisler, H. J., Model Theory, North-Holland, Amsterdam, 1956.Google Scholar
[D 1] Delon, F., Cours manuscrits sur la théorie des modèles, Université Paris VII, Paris, 1983.Google Scholar
[D 2] Chang, C. C. and Keisler, H. J., Extensions séparees et immédiates de corps valués, this Journal, vol. 53 (1988), pp. 421–428.Google Scholar
[D 3] Chang, C. C. and Keisler, H. J., Paires de corps réels clos, Séeminaire généeral de logique, 1983–1984, Publications Mathématiques de l’Université Paris VII, no. 27, Universite Paris VII, Paris, 1984, pp. 185–195.Google Scholar
[F-J] Fried, M. and Jarden, M., Field arithmetic, Springer-Verlag, Berlin, 1986.CrossRefGoogle Scholar
[K] Keisler, H. J., Complete theories of algebraically closed fields with distinguished subfields, Michigan Mathematical Journal, vol. 11 (1964), pp. 71–81.CrossRefGoogle Scholar
[La 1] Lang, S., Introduction to algebraic geometry, Interscience, New York, 1958.Google Scholar
[La 2] Lang, S., Algebra, Addison-Wesley, Reading, Massachussets, 1965.Google Scholar
[L] Leloup, G., Théories complètes de paires de corps valués henseliens, this Journal, vol. 55 (1990), pp. 323–339.Google Scholar
[L′] Leloup, G., Une démonstration du théoréme d’ Ax-Kochen-Ershov, Séminaire du laboratoire de logique, algorithmique et informatique clermontois, (Université d’ Auvergne Clermont 1, France), Vol. 1 (1989–1990) Clermont-Ferrand, 1990, exposé 9, pp. 98–112.Google Scholar
[M] Macintyre, A. J., Classifying pairs of real closed fields, Ph.D. thesis, Stanford University, Stanford, California, 1968.Google Scholar
[M-MK-vdD] Macintyre, A., Mckenna, K., and Van Den Dries, L., Elimination of quantifiers in algebraic structures, Advances in Mathematics, vol. 47 (1983), pp. 74–87.CrossRefGoogle Scholar
[P] Prestel, A., Lectures on formally real fields, Monografias de Matemática, vol. 22, Instituto de Matematica Pura e Aplicada, Rio de Janeiro, 1975.Google Scholar
[Ri] Ribenboim, P., Théorie des valuations, Les Presses de l’ Université de Montréal, Montréal, 1964.Google Scholar
[Ro 1] Robinson, A., Complete theories, North-Holland, Amsterdam, 1956.Google Scholar
[Ro 2] Robinson, A., Solution of a problem of Tarski, Fundamenta Mathematicae, vol. 47 (1959), pp. 179–204.CrossRefGoogle Scholar
[S 1] Shoenfield, J. R., Mathematical logic, Addison-Wesley, Reading, Massachusetts, 1967.Google Scholar
[S 2] Shoenfield, J. R., Symposia mathematica (1NDAM), vol. 5, Academic Press, London, 1971, pp. 173–176.Google Scholar
[W 1] Weispfenning, V., On the elementary theory of Hensel fields, Annals of Mathematical Logic, vol. 10 (1976), pp. 59–93.CrossRefGoogle Scholar
[W 2] Weispfenning, V., Quantifier elimination and decision procedure for valued fields, Models and sets, Logic Colloquium ’ 83, part 1 (Aachen 1983), Lecture Notes in Mathematics, vol. 1103, Springer-Verlag, Berlin, 1984, pp. 419–472.Google Scholar