Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kanovei, Vladimir
1998.
Ulm Classification of Analytic Equivalence Relations in Generic Universes.
Mathematical Logic Quarterly,
Vol. 44,
Issue. 3,
p.
287.
Hjorth, Greg
1999.
Orbit cardinals: On the effective cardinalities arising as quotient spaces of the formX/G whereG acts on a Polish spaceX.
Israel Journal of Mathematics,
Vol. 111,
Issue. 1,
p.
221.
Hjorth, Greg
2010.
Handbook of Set Theory.
p.
297.
Rathjen, Michael
2011.
2010 European Summer Meeting of the Association for Symbolic Logic. Logic Colloquium '10.
The Bulletin of Symbolic Logic,
Vol. 17,
Issue. 2,
p.
272.
Andretta, Alessandro
and
Louveau, Alain
2011.
Wadge Degrees and Projective Ordinals The Cabal Seminar Volume II.
p.
3.
Schlicht, Philipp
2014.
Thin equivalence relations and inner models.
Annals of Pure and Applied Logic,
Vol. 165,
Issue. 10,
p.
1577.
Ketchersid, Richard
Larson, Paul
and
Zapletal, Jindřich
2016.
Ramsey ultrafilters and Countable-to-one Uniformization.
Topology and its Applications,
Vol. 213,
Issue. ,
p.
190.
2017.
Chan, William
and
Jackson, Stephen
2019.
L(R) with determinacy satisfies the Suslin hypothesis.
Advances in Mathematics,
Vol. 346,
Issue. ,
p.
305.
Chan, William
and
Jackson, Stephen
2021.
Cardinality of wellordered disjoint unions of quotients of smooth equivalence relations.
Annals of Pure and Applied Logic,
Vol. 172,
Issue. 8,
p.
102988.
Andretta, Alessandro
and
Motto Ros, Luca
2022.
Souslin quasi-orders and bi-embeddability of uncountable structures.
Memoirs of the American Mathematical Society,
Vol. 277,
Issue. 1365,
Chan, William
Jackson, Stephen
and
Trang, Nam
2023.
More definable combinatorics around the first and second uncountable cardinals.
Journal of Mathematical Logic,
Vol. 23,
Issue. 03,


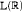 either admits a wellordered separating family or continuously reduces
either admits a wellordered separating family or continuously reduces 