Article contents
CODING IN GRAPHS AND LINEAR ORDERINGS
Published online by Cambridge University Press: 18 June 2020
Abstract
There is a Turing computable embedding 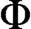 $\Phi $
of directed graphs
$\Phi $
of directed graphs 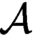 $\mathcal {A}$
in undirected graphs (see [15]). Moreover, there is a fixed tuple of formulas that give a uniform effective interpretation; i.e., for all directed graphs
$\mathcal {A}$
in undirected graphs (see [15]). Moreover, there is a fixed tuple of formulas that give a uniform effective interpretation; i.e., for all directed graphs 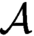 $\mathcal {A}$
, these formulas interpret
$\mathcal {A}$
, these formulas interpret 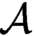 $\mathcal {A}$
in
$\mathcal {A}$
in 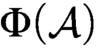 $\Phi (\mathcal {A})$
. It follows that
$\Phi (\mathcal {A})$
. It follows that 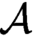 $\mathcal {A}$
is Medvedev reducible to
$\mathcal {A}$
is Medvedev reducible to 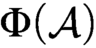 $\Phi (\mathcal {A})$
uniformly; i.e.,
$\Phi (\mathcal {A})$
uniformly; i.e., 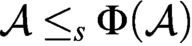 $\mathcal {A}\leq _s\Phi (\mathcal {A})$
with a fixed Turing operator that serves for all
$\mathcal {A}\leq _s\Phi (\mathcal {A})$
with a fixed Turing operator that serves for all 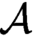 $\mathcal {A}$
. We observe that there is a graph G that is not Medvedev reducible to any linear ordering. Hence, G is not effectively interpreted in any linear ordering. Similarly, there is a graph that is not interpreted in any linear ordering using computable
$\mathcal {A}$
. We observe that there is a graph G that is not Medvedev reducible to any linear ordering. Hence, G is not effectively interpreted in any linear ordering. Similarly, there is a graph that is not interpreted in any linear ordering using computable 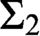 $\Sigma _2$
formulas. Any graph can be interpreted in a linear ordering using computable
$\Sigma _2$
formulas. Any graph can be interpreted in a linear ordering using computable 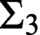 $\Sigma _3$
formulas. Friedman and Stanley [4] gave a Turing computable embedding L of directed graphs in linear orderings. We show that there is no fixed tuple of
$\Sigma _3$
formulas. Friedman and Stanley [4] gave a Turing computable embedding L of directed graphs in linear orderings. We show that there is no fixed tuple of 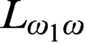 $L_{\omega _1\omega }$
-formulas that, for all G, interpret the input graph G in the output linear ordering
$L_{\omega _1\omega }$
-formulas that, for all G, interpret the input graph G in the output linear ordering 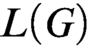 $L(G)$
. Harrison-Trainor and Montalbán [7] have also shown this, by a quite different proof.
$L(G)$
. Harrison-Trainor and Montalbán [7] have also shown this, by a quite different proof.
MSC classification
- Type
- Articles
- Information
- Copyright
- © The Association for Symbolic Logic 2020
References
REFERENCES
- 3
- Cited by


