Categories of frames for modal logic

Extract

§1. A complete atomic modal algebra (CAMA) is a complete atomic Boolean algebra with an additional completely additive unary operator. A (Kripke) frame is just a binary relation on a nonempty set. If 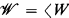is a frame, then 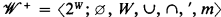is a CAMA, where mX = {y ∣ (∃x)(y < x Є X)}; and if 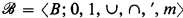is a CAMA then 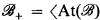is a frame, where 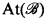is the set of atoms of 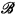and b₁ < b₂ ⇔ b₁ ∩ mb₂ ≠∅.

Now 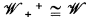, and 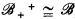the validity of a modal formula on 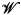is equivalent to the satisfaction of a modal algebra polynomial identity by 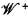and conversely, so the validity-preserving constructions on frames ought to be in some sense equivalent to the identity-preserving constructions on CAMA's. The former are important for modal logic, and many of the results of universal algebra apply to the latter, so it is worthwhile to fix precisely the sense of the equivalence.

The most important identity-preserving constructions on CAMA's can be described in terms of homomorphisms and complete homomorphisms. Let 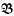and 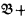be the categories of CAMA's with homomorphisms and complete homomorphisms, respectively. We shall define categories 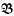and 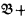of frames with appropriate morphisms, and show them to be dual respectively to 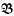and 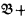. Then we shall consider certain identity-preserving constructions on CAMA's and attempt to describe the corresponding validity-preserving constructions on frames.

The proofs of duality involve some rather detailed calculations, which have been omitted. All the category theory a reader needs to know is in the first twenty pages of [7].