Article contents
An improved prenex normal form1
Published online by Cambridge University Press: 12 March 2014
Extract
Let ℒ be the set of all formulas of a given first order predicate logic (with or without identity). For each positive integer n, let ℒn be the set of all formulas φ in ℒ logically equivalent to a formula of the form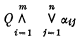
where Q is a (possibly empty) string of quantifiers, m is a positive integer, and each αij is either an atomic formula or the negation of an atomic formula.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1962
Footnotes
The work of the first named author was supported by a research grant from the National Science Foundation. The work of the second named author was supported by a National Science Foundation Cooperative Fellowship.
References
2 Before arriving at the final result, the bound on the length of the disjunctions in the improved normal form took, with the passage of time, the following values (in the opinion of the authors): 3·p + 2p, 4·p, 3·p + 2p, 5·p, 3·p, max(3, p), and finally, in the case of logic with identity, max (2, p). The authors became interested in this problem through their investigations on reduced products in the theory of models. Chronologically, the results of § 2 preceded those of § 1. In the light of the methods of § 1, the proofs in § 2 were considerably simplified.
- 8
- Cited by


