Research Article
On the instability of a spatially confined electron beam in a magnetized plasma
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 193-212
The microinstabilities of a high-β plasma flow with a non-uniform velocity profile
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 385-407
Super-ion-beam accelerator for the ignition of thermonuclear reactions
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 1-14
Kelvin–Helmholtz problem in a rotating Hall plasma
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 213-219
Dispersion formulae for waves in a magneto-active relativistic plasma
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 409-420
Nonlinear phenomena in plasma with relativistic high-frequency electron motion
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 15-23
Langmuir turbulence as a critical phenomenon. Part 2. Application of the dynamical renormalization group method
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 421-443
Low-frequency electrostatic instability due to anti-loss-cone electrons
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 221-227
Parametric instability driven by density modulation in velocity space
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 25-37
Low-frequency linear response of a cylindrical tokamak with arbitrary cross-section to ‘helical’ perturbations
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 229-236
The stability properties of cylindrical force-free fields: effect of an external potential field
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 39-53
Modulational instability of electrostatic ion cyclotron wave in a two-electron-temperature plasma
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 445-452
Longitudinal electron modes in plasma
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 237-250
Nonlinear coupling of five waves in non-uniform streaming plasma
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 55-63
Plasma equilibrium in toroidal l = 3 stellarators
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 453-478
Re-ionization of a partially ionized plasma by an Alfvén wave of moderate amplitude
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 65-74
The stability of parallel flow of a multi-component plasma
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 251-264
Convective instability of a plasma slab in a magnetic field
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 479-482
Effect of collisions on the relativistic electromagnetic instability
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 483-488
Energy loss of relativistic electrons in plasma in accordance with covariant Fokker–Planck formalism
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 75-88

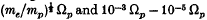 (ω
(ω