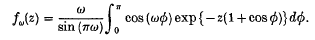Research Article
An electron thermal instability in a resistive non-equilibrium fully ionised plasma
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 1-14
On the Dupree–Weinstock turbulence theory
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 177-198
Self-consistent Vlasov equilibria for intense hollow relativistic electron beams
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 353-364
Application of the theory of mixing systems to nonlinear Landau damping
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 365-379
Generation and radiation of second harmonics by s-polarized electromagnetic waves incident on a narrow inhomogeneous plasma layer
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 15-20
An analytical study of the oblique echo model for the topside plasma resonance
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 199-216
An analytical study of the oblique echo model for the topside upper hybrid resonance
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 217-232
Thermal relaxation of a two-dimensional plasma in a d.c. magnetic field. Part 1. Theory
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 21-26
Energy transfer equation and universal spectrum of ion–acoustic wave turbulence
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 381-393
Two-stream instability in plasmas for arbitrary propagation
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 395-403
Filament model for a stationary field electron ring accelerator: the generalized Bernstein—Green—Kruskal problem
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 233-269
Thermal relaxation of a two-dimensional plasma in a d.c. magnetic field. Part 2. Numerical simulation
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 27-31
Second harmonic generation using spatially varying static electron number density in a magnetoplasma
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 405-415
Wave propagation in a moving plasma. Part 2. Wave propagation along, and plasma motion normal to, the magnetic field
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 271-278
Effect of Hall current on the instability of an anisotropic plasma jet
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 33-43
Pitch angle and energy diffusion coefficients from resonant interactions with ion–cyclotron and whistler waves
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 417-432
Diffusion of resonance particles in strong plasma turbulence
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 279-286
General relations for resonant particle diffusion in pitch angle and energy
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 45-49
The magnetoplasma dispersion function: some mathematical properties
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 51-59
Ion–acoustic instability of the positive column
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 433-444

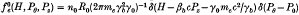 , where H, P
, where H, P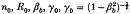 , and P
, and P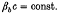 , and the beam density profile
, and the beam density profile 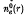 is hollow with inner and outer radii, R
is hollow with inner and outer radii, R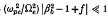 . The two cases, P
. The two cases, P in the large
in the large