Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-18T10:42:46.340Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonlinear equilibrium and stability analysis of rippled, partially neutralized, magnetically focused electron beams

Published online by Cambridge University Press:  13 March 2009

S. Cuperman  and
F. Petran
S. Cuperman
Affiliation:
Department of Physics and Astronomy, Tel Aviv University, Tel Aviv 69978, Israel
F. Petran
Affiliation:
Department of Physics and Astronomy, Tel Aviv University, Tel Aviv 69978, Israel
Get access Rights & Permissions [Opens in a new window]

Abstract

In the first part of this work a higher-order solution of the anharmonic oscillator equation describing the nonlinear rippled equilibrium state of magnetically focused, partially neutralized electron beams is given. Thus, using the method of harmonic balance, we derive a ripple-&litude solution of the form

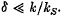
where ø=ω1t+β0,ω1 being the nonlinear proper frequency and β0 a phase shift depending on the initial conditions. In the second part of the work we carry out a stability analysis of the nonlinear equilibrium state found in the first part with respect to long- and short-wavelength surface space-charge perturbations. In the framework of a local approximation the wave equation for the rippled beam is found to be a Hill type of equation which contains harmonic terms up to cos 3kSz (ks is the wavenumber of the ripple). This equation is solved by a resonant-mode coupling method; coupling of fast-fast, slow-slow and slow-fast waves is considered. The growth rates and band widths for different possible wave couplings are derived and compared.

Type
Research Article
Information
Journal of Plasma Physics , Volume 27 , Issue 3 , June 1982 , pp. 453 - 471
Copyright
Copyright © Cambridge University Press 1982

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bekefi, G. 1966 Radiation Processes in Plasmas. Wiley.Google Scholar
Bernstein, W., Leinbach, H., Cohen, H., Wilson, P. S., Davis, T. N., Hallinan, T., Baker, B., Martz, J., Zeimke, R. & Huber, W. 1975 J. Geophys. Res. 80, 4375.CrossRefGoogle Scholar
Cunningham, W. J. 1958 Introduction to Non-linear Analysis. McGraw-Hill.Google Scholar
Cuperman, S. & Petran, F. 1981 a J. Plaslna Phys. 25, 215.CrossRefGoogle Scholar
Cuperman, S. & Petran, F. 1981 b J.Plasma Phys. 26, 267.CrossRefGoogle Scholar
Davidson, R. C. 1974 Theory of Non-neutral Plasrnas. Benjamin.Google Scholar
Mahaffey, R. A. 1976 Phys. Fluids, 19, 1387.CrossRefGoogle Scholar
Mahaffey, R. A., Batchelor, D. B. & Trivelpiece, A. W. 1976 J. Appl. Phys. 47, 4464.CrossRefGoogle Scholar
Mahaffey, R. A., Goldstein, S. A., Davidson, R. C. & Trivelpiece, A. W. 1975 Phys. Rev. Lett. 35, 1439.CrossRefGoogle Scholar
Mahaffey, R. A., Marsh, S. J., Golden, J. & Kapetanakos, C. A. 1977 Appl. Phys. Lett. 30, 449.CrossRefGoogle Scholar
Mahaffey, R. A. & Trivelpiece, A. W. 1977 Phys. Fluids, 20, 469.CrossRefGoogle Scholar
Morse, P. M. & Fesrbacr, H. 1953 Methods of Theoretical Physios, vol. 2, p. 1092. McGraw-Hill.Google Scholar
Nayfeh, A. & Mook, T. D. 1979 Nonlinear Oscillations. Wiley.Google Scholar
Theiss, A. J., Mahaffey, R. A. & Trivelpiece, A. W. 1975 Phys. Rev. Leit. 35, 1436.CrossRefGoogle Scholar
Theiss, A. J., Mahaffey, R. A. & Trivelpiece, A. W. 1977 Phys. Fluids, 20, 785.CrossRefGoogle Scholar
Tien, P. K. 1977 Rev. Mod. Phys. 49, 361.CrossRefGoogle Scholar