Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-30T19:01:17.888Z Has data issue: false hasContentIssue false
  • English
  • Français

Kinetic energy corrections for the free electrons in a high-frequency, fully-ionized plasma

Published online by Cambridge University Press:  13 March 2009

Gheorghe Lupu
Gheorghe Lupu
Affiliation:
Institute of Marine, Constantza, Romania
Get access Rights & Permissions [Opens in a new window]

Extract

It is found that, for a fully-ionized, homogeneous plasma in a high-frequency electric field, the fundamental term 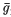1 in the kinetic-energy correction is defined by the intensity and frequency of the electric field and by the collision frequency v1. We obtain the Debye–Hükel energy correction in 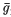2, too, as did Theimer & Wright, but this term is much smaller than 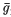1, and its coefficient is no longer a constant.

Type
Articles
Information
Journal of Plasma Physics , Volume 13 , Issue 1 , February 1975 , pp. 167 - 172
Copyright
Copyright © Cambridge University Press 1975

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abraham-shrauner, B. 1970 J. Plasma Phys. 4, 323.Google Scholar
Harrison, E. R. 1962 Plasma Phys. 4, 7.Google Scholar
Harrison, E. R. 1967 Plasma Phys. 9, 183.CrossRefGoogle Scholar
Jancel, R. 1968 Nuovo Cimento Suppl. 6, 1329.Google Scholar
Jancel, R. & Kahan, T. 1963 Electrodinamique des plasmas, vol. 1. Paris: Dunod.Google Scholar
Lupu, G. 1969 Bull. Math. de Soc. Sci. Math. de la R.S. de Roumanie, 13, 349.Google Scholar
Lupu, G. 1970 a Rev. Roum. Math. Pures et Appl. 15, 871.Google Scholar
Lupu, G. 1970 b Rev. Roum. Math. Pures et Appl. 15, 1011.Google Scholar
Lupu, G. 1972 Rev. Roum. Math. Pures et Appl. 17, 731.Google Scholar
Lupu, G. & Mustata, C. 1973 Rev. Roum. Phys. 18, 365.Google Scholar
Theimer, O. & Wright, T. 1969 Phys. Rev. 180, 308.CrossRefGoogle Scholar
Wright, T. & Theimer, O. 1970 Phys. Fluids, 13, 859.Google Scholar