1 Introduction
The most developed concepts for achieving controlled thermonuclear fusion are the tokamak and stellarator. Both the tokamak and the stellarator utilize a strong toroidal magnetic field to confine a hot plasma in which fusion reactions take place.
When such a plasma is in a steady state, loss of particles and energy mainly occurs as a result of micro-turbulence, collisions or direct losses of particles on unconfined orbits. The two latter processes – and the resulting transport of particles and heat – are referred to as collisional transport, and can be modelled within the framework of drift kinetics. Historically this is the dominant transport channel in the core of stellarators because of the large transport due to particles on unconfined orbits (Beidler et al. Reference Beidler, Brakel, Burhenn, Dinklage, Erckmann, Feng, Geiger, Hartmann, Hirsch and Jaenicke2012).
Collisional transport can be further separated into two additive components: classical transport, which is due to the gyro-motion of particles around the magnetic field lines, and neoclassical transport, which is due to the complex orbits carried out by the centre of gyration as it moves in the magnetic field. The latter typically leads to much larger transport than the former (Pfirsch & Schlüter Reference Pfirsch and Schlüter1962), and also accounts for the unconfined orbits in stellarators, with a very strong unfavourable scaling towards reactor-relevant high temperatures. Thus, much effort has been devoted to reducing the neoclassical transport in stellarators – resulting in optimized stellarators such as Wendelstein 7-X (W7-X) (Nührenberg & Zille Reference Nührenberg and Zille1986) – while classical transport is often neglected.
However, it has not been widely appreciated that, as a result of optimizing for low neoclassical transport and Pfirsch–Schlüter current, the neoclassical transport of impurities in W7-X can now be comparable to the often neglected classical transport. The main purpose of the present note is to raise attention to this circumstance.
To understand why the classical transport is relevant in an optimized stellarator, we employ recent analytical results on neoclassical transport for a collisional impurity (Braun & Helander Reference Braun and Helander2010; Helander et al. Reference Helander, Newton, Mollén and Smith2017; Newton et al. Reference Newton, Helander, Mollén and Smith2017) to show that the ratio of classical to neoclassical fluxes is proportional to a geometrical factor (2.1), which turns out to be larger than one in W7-X.
Motivated by these results, we present a general expression for the classical transport, using the linearized Fokker–Planck operator and allowing for an arbitrary number of species. The employed collision operator is frequently used in modern neoclassical solvers, and the results can thus be directly compared with the output from such codes. In the final sections, we look at a few example magnetic configurations, where we compare the magnitude of the classical transport to that of the neoclassical transport calculated with the Sfincs Footnote 1 drift-kinetic solver (Landreman et al. Reference Landreman, Smith, Mollén and Helander2014), and investigate the collisionality dependence of the ratio of classical to neoclassical transport.
2 Motivation
Before performing a detailed analysis, it is useful to consider a simple (but experimentally relevant) limit, where the importance of classical transport in a stellarator is apparent. For this purpose, we summarize results from earlier work (Braun & Helander Reference Braun and Helander2010; Helander et al. Reference Helander, Newton, Mollén and Smith2017; Buller et al. Reference Buller, Smith, Helander, Mollén, Newton and Pusztai2018).
At fusion-relevant temperatures, the bulk hydrogen species of the confined plasma will be in a low-collisionality regime. However, as the collisionality increases with charge, high-
![]() $Z$
impurities (with
$Z$
impurities (with
![]() $Z$
being the charge number) can still have high collisionality. Such impurities can occur, for example, in experiments using tungsten plasma-facing components, which is the favoured material for the divertor of future fusion reactors (Bolt et al.
Reference Bolt, Barabash, Federici, Linke, Loarte, Roth and Sato2002). These plasmas will thus be in a mixed-collisionality regime, with low-collisionality bulk and high-collisionality impurity ions.
$Z$
being the charge number) can still have high collisionality. Such impurities can occur, for example, in experiments using tungsten plasma-facing components, which is the favoured material for the divertor of future fusion reactors (Bolt et al.
Reference Bolt, Barabash, Federici, Linke, Loarte, Roth and Sato2002). These plasmas will thus be in a mixed-collisionality regime, with low-collisionality bulk and high-collisionality impurity ions.
In this regime, the ratio of classical to neoclassical impurity particle fluxes calculated from the mass-ratio expanded collision operator is given by a purely geometrical factor (Buller et al. Reference Buller, Smith, Helander, Mollén, Newton and Pusztai2018)
Here,
![]() $\unicode[STIX]{x1D713}$
is a radial coordinate (a flux-surface label),
$\unicode[STIX]{x1D713}$
is a radial coordinate (a flux-surface label),
![]() $\langle \cdot \rangle$
is the flux-surface average,
$\langle \cdot \rangle$
is the flux-surface average,
![]() $\unicode[STIX]{x1D71E}_{z}$
is the flux of impurity ions,
$\unicode[STIX]{x1D71E}_{z}$
is the flux of impurity ions,
![]() $\langle \unicode[STIX]{x1D71E}_{z}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}\rangle ^{\text{(N)C}}$
is the radial (neo)classical impurity flux averaged over the flux surface,
$\langle \unicode[STIX]{x1D71E}_{z}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}\rangle ^{\text{(N)C}}$
is the radial (neo)classical impurity flux averaged over the flux surface,
![]() $\boldsymbol{B}$
is the magnetic field,
$\boldsymbol{B}$
is the magnetic field,
![]() $B=|\boldsymbol{B}|$
, and
$B=|\boldsymbol{B}|$
, and
![]() $\boldsymbol{j}$
is the current density, here defined by
$\boldsymbol{j}$
is the current density, here defined by
![]() $\boldsymbol{j}\times \boldsymbol{B}=\unicode[STIX]{x1D735}p(\unicode[STIX]{x1D713})$
,
$\boldsymbol{j}\times \boldsymbol{B}=\unicode[STIX]{x1D735}p(\unicode[STIX]{x1D713})$
,
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{j}=0$
; with
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{j}=0$
; with
![]() $j_{\Vert }$
and
$j_{\Vert }$
and
![]() $j_{\bot }$
being the current components parallel and perpendicular to
$j_{\bot }$
being the current components parallel and perpendicular to
![]() $\boldsymbol{B}$
, and
$\boldsymbol{B}$
, and
![]() $p$
the total pressure.
$p$
the total pressure.
Equation (2.1) also enters into the ratio of classical and neoclassical transport at yet higher collisionalities: in the Pfirsch–Schlüter regime, where both bulk and impurity ions are collisional. This can be shown using the expression for neoclassical transport derived by Braun & Helander (Reference Braun and Helander2010) together with the expression for classical transport in, for example, Buller et al. (Reference Buller, Smith, Helander, Mollén, Newton and Pusztai2018). For stellarators optimized for low
![]() $j_{\Vert }/j_{\bot }$
(such as W7-X), the (2.1) ratio will be large and classical transport will thus dominate at high collisionality. This will be verified by numerical simulations in § 4.
$j_{\Vert }/j_{\bot }$
(such as W7-X), the (2.1) ratio will be large and classical transport will thus dominate at high collisionality. This will be verified by numerical simulations in § 4.
3 Linearized Fokker–Planck operator
In this section, we write down the classical particle and heat transport due to a linearized Fokker–Planck operator. The flux-surface averaged radial classical transport of particles and energy is given by
where we have introduced the friction force and energy-weighted friction force
Here,
![]() $C[f_{a}]=\sum _{b}C_{ab}[f_{a},f_{b}]$
is the Fokker–Planck collision operator, accounting for the collisions of all species ‘
$C[f_{a}]=\sum _{b}C_{ab}[f_{a},f_{b}]$
is the Fokker–Planck collision operator, accounting for the collisions of all species ‘
![]() $b$
’ with species ‘
$b$
’ with species ‘
![]() $a$
’;
$a$
’;
![]() $f_{a}$
the distribution function of species ‘
$f_{a}$
the distribution function of species ‘
![]() $a$
’, with mass
$a$
’, with mass
![]() $m_{a}$
and charge
$m_{a}$
and charge
![]() $Z_{a}e$
, with
$Z_{a}e$
, with
![]() $e$
the elementary charge; the integral is over all velocities
$e$
the elementary charge; the integral is over all velocities
![]() $\boldsymbol{v}$
. In a confined plasma, the distribution functions are close to a Maxwell–Boltzmann distribution
$\boldsymbol{v}$
. In a confined plasma, the distribution functions are close to a Maxwell–Boltzmann distribution
![]() $f_{a0}$
, such that
$f_{a0}$
, such that
![]() $f_{a}=f_{a0}+f_{a1}$
, and
$f_{a}=f_{a0}+f_{a1}$
, and
![]() $f_{a1}$
satisfies
$f_{a1}$
satisfies
![]() $f_{a1}/f_{a0}\ll 1$
. For later reference, we also define the classical conductive heat flux
$f_{a1}/f_{a0}\ll 1$
. For later reference, we also define the classical conductive heat flux
![]() $q_{a}^{\text{C}}=Q_{a}^{\text{C}}-(5/2)T_{a}\unicode[STIX]{x1D6E4}_{a}^{\text{C}}$
, where
$q_{a}^{\text{C}}=Q_{a}^{\text{C}}-(5/2)T_{a}\unicode[STIX]{x1D6E4}_{a}^{\text{C}}$
, where
![]() $T_{a}$
is the temperature of species ‘
$T_{a}$
is the temperature of species ‘
![]() $a$
’.
$a$
’.
For a magnetized plasma, it is useful to separate out the dependence of the distribution function on the gyro-phase. Only the gyro-phase-dependent part of
![]() $f$
, which we denote by
$f$
, which we denote by
![]() $\tilde{f}$
, contributes to
$\tilde{f}$
, contributes to
![]() $\boldsymbol{R}$
and
$\boldsymbol{R}$
and
![]() $\boldsymbol{G}$
perpendicular to the magnetic field, and thus to the classical fluxes (3.1)–(3.2). For a magnetized plasma with an isotropic Maxwellian, it is well known that (Hazeltine Reference Hazeltine1973)
$\boldsymbol{G}$
perpendicular to the magnetic field, and thus to the classical fluxes (3.1)–(3.2). For a magnetized plasma with an isotropic Maxwellian, it is well known that (Hazeltine Reference Hazeltine1973)
where
![]() $\unicode[STIX]{x1D746}_{a}=\boldsymbol{B}\times \boldsymbol{v}m_{a}/(Z_{a}eB^{2})$
is the gyro-radius vector.
$\unicode[STIX]{x1D746}_{a}=\boldsymbol{B}\times \boldsymbol{v}m_{a}/(Z_{a}eB^{2})$
is the gyro-radius vector.
With (3.5), we can readily evaluate the classical transport given by (3.1)–(3.4). Lately in stellarator research, the importance of flux-surface variation of the electrostatic potential has been recognized (García-Regaña et al.
Reference García-Regaña, Beidler, Kleiber, Helander, Mollén, Alonso, Landreman, Maaßberg, Smith and Turkin2017); such effects can be incorporated into the classical transport by including the flux-surface varying part of the potential in the Maxwell–Boltzmann distribution
![]() $f_{0}$
(Hinton & Wong Reference Hinton and Wong1985)
$f_{0}$
(Hinton & Wong Reference Hinton and Wong1985)
where
![]() $\unicode[STIX]{x1D6F7}$
is the electrostatic potential,
$\unicode[STIX]{x1D6F7}$
is the electrostatic potential,
![]() $\tilde{\unicode[STIX]{x1D6F7}}=\unicode[STIX]{x1D6F7}-\langle \unicode[STIX]{x1D6F7}\rangle$
and we have introduced the pseudo-density
$\tilde{\unicode[STIX]{x1D6F7}}=\unicode[STIX]{x1D6F7}-\langle \unicode[STIX]{x1D6F7}\rangle$
and we have introduced the pseudo-density
with
![]() $n$
the density. In terms of gradients of
$n$
the density. In terms of gradients of
![]() $\unicode[STIX]{x1D702}$
,
$\unicode[STIX]{x1D702}$
,
![]() $T$
and
$T$
and
![]() $\unicode[STIX]{x1D6F7}$
, the gradient in (3.5) thus becomes,
$\unicode[STIX]{x1D6F7}$
, the gradient in (3.5) thus becomes,
With this
![]() $\unicode[STIX]{x1D735}f_{0}$
, the resulting classical fluxes can be calculated using Braginskii matrices (as in, for example, Newton & Helander (Reference Newton and Helander2006)), resulting in
$\unicode[STIX]{x1D735}f_{0}$
, the resulting classical fluxes can be calculated using Braginskii matrices (as in, for example, Newton & Helander (Reference Newton and Helander2006)), resulting in
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}_{a}^{\text{C}} & = & \displaystyle {\displaystyle \frac{m_{a}}{Z_{a}e^{2}}}\mathop{\sum }_{b}{\displaystyle \frac{1}{\unicode[STIX]{x1D70F}_{ab}n_{b}}}\left\{\left\langle n_{a}n_{b}{\displaystyle \frac{|\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}|^{2}}{B^{2}}}\right\rangle M_{ab}^{00}\left({\displaystyle \frac{T_{a}}{Z_{a}}}{\displaystyle \frac{\text{d}\ln \unicode[STIX]{x1D702}_{a}}{\text{d}\unicode[STIX]{x1D713}}}-{\displaystyle \frac{T_{b}}{Z_{b}}}{\displaystyle \frac{\text{d}\ln \unicode[STIX]{x1D702}_{b}}{\text{d}\unicode[STIX]{x1D713}}}\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\,\left\langle n_{a}n_{b}{\displaystyle \frac{|\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}|^{2}}{B^{2}}}e\tilde{\unicode[STIX]{x1D6F7}}\right\rangle M_{ab}^{00}\left({\displaystyle \frac{\text{d}\ln T_{a}}{\text{d}\unicode[STIX]{x1D713}}}-{\displaystyle \frac{\text{d}\ln T_{b}}{\text{d}\unicode[STIX]{x1D713}}}\right)\nonumber\\ \displaystyle & & \displaystyle \left.+\left\langle n_{a}n_{b}{\displaystyle \frac{|\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}|^{2}}{B^{2}}}\right\rangle \left[(M_{ab}^{00}-M_{ab}^{01}){\displaystyle \frac{T_{a}}{Z_{a}}}{\displaystyle \frac{\text{d}\ln T_{a}}{\text{d}\unicode[STIX]{x1D713}}}-\left(M_{ab}^{00}-{\displaystyle \frac{m_{a}T_{b}}{m_{b}T_{a}}}M_{ab}^{01}\right){\displaystyle \frac{T_{b}}{Z_{b}}}{\displaystyle \frac{\text{d}\ln T_{b}}{\text{d}\unicode[STIX]{x1D713}}}\right]\right\},\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}_{a}^{\text{C}} & = & \displaystyle {\displaystyle \frac{m_{a}}{Z_{a}e^{2}}}\mathop{\sum }_{b}{\displaystyle \frac{1}{\unicode[STIX]{x1D70F}_{ab}n_{b}}}\left\{\left\langle n_{a}n_{b}{\displaystyle \frac{|\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}|^{2}}{B^{2}}}\right\rangle M_{ab}^{00}\left({\displaystyle \frac{T_{a}}{Z_{a}}}{\displaystyle \frac{\text{d}\ln \unicode[STIX]{x1D702}_{a}}{\text{d}\unicode[STIX]{x1D713}}}-{\displaystyle \frac{T_{b}}{Z_{b}}}{\displaystyle \frac{\text{d}\ln \unicode[STIX]{x1D702}_{b}}{\text{d}\unicode[STIX]{x1D713}}}\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\,\left\langle n_{a}n_{b}{\displaystyle \frac{|\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}|^{2}}{B^{2}}}e\tilde{\unicode[STIX]{x1D6F7}}\right\rangle M_{ab}^{00}\left({\displaystyle \frac{\text{d}\ln T_{a}}{\text{d}\unicode[STIX]{x1D713}}}-{\displaystyle \frac{\text{d}\ln T_{b}}{\text{d}\unicode[STIX]{x1D713}}}\right)\nonumber\\ \displaystyle & & \displaystyle \left.+\left\langle n_{a}n_{b}{\displaystyle \frac{|\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}|^{2}}{B^{2}}}\right\rangle \left[(M_{ab}^{00}-M_{ab}^{01}){\displaystyle \frac{T_{a}}{Z_{a}}}{\displaystyle \frac{\text{d}\ln T_{a}}{\text{d}\unicode[STIX]{x1D713}}}-\left(M_{ab}^{00}-{\displaystyle \frac{m_{a}T_{b}}{m_{b}T_{a}}}M_{ab}^{01}\right){\displaystyle \frac{T_{b}}{Z_{b}}}{\displaystyle \frac{\text{d}\ln T_{b}}{\text{d}\unicode[STIX]{x1D713}}}\right]\right\},\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle q_{a}^{\text{C}} & = & \displaystyle -{\displaystyle \frac{T_{a}m_{a}}{Z_{a}e^{2}}}\mathop{\sum }_{b}{\displaystyle \frac{1}{\unicode[STIX]{x1D70F}_{ab}n_{b}}}\left\{\left\langle n_{a}n_{b}{\displaystyle \frac{|\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}|^{2}}{B^{2}}}\right\rangle M_{ab}^{01}\left({\displaystyle \frac{T_{a}}{Z_{a}}}{\displaystyle \frac{\text{d}\ln \unicode[STIX]{x1D702}_{a}}{\text{d}\unicode[STIX]{x1D713}}}-{\displaystyle \frac{T_{b}}{Z_{b}}}{\displaystyle \frac{\text{d}\ln \unicode[STIX]{x1D702}_{b}}{\text{d}\unicode[STIX]{x1D713}}}\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\,\left\langle n_{a}n_{b}{\displaystyle \frac{|\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}|^{2}}{B^{2}}}e\tilde{\unicode[STIX]{x1D6F7}}\right\rangle M_{ab}^{01}\left({\displaystyle \frac{\text{d}\ln T_{a}}{\text{d}\unicode[STIX]{x1D713}}}-{\displaystyle \frac{\text{d}\ln T_{b}}{\text{d}\unicode[STIX]{x1D713}}}\right)\nonumber\\ \displaystyle & & \displaystyle \left.+\left\langle n_{a}n_{b}{\displaystyle \frac{|\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}|^{2}}{B^{2}}}\right\rangle \left[(M_{ab}^{01}-M_{ab}^{11}){\displaystyle \frac{T_{a}}{Z_{a}}}{\displaystyle \frac{\text{d}\ln T_{a}}{\text{d}\unicode[STIX]{x1D713}}}-(M_{ab}^{01}+N_{ab}^{11}){\displaystyle \frac{T_{b}}{Z_{b}}}{\displaystyle \frac{\text{d}\ln T_{b}}{\text{d}\unicode[STIX]{x1D713}}}\right]\right\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle q_{a}^{\text{C}} & = & \displaystyle -{\displaystyle \frac{T_{a}m_{a}}{Z_{a}e^{2}}}\mathop{\sum }_{b}{\displaystyle \frac{1}{\unicode[STIX]{x1D70F}_{ab}n_{b}}}\left\{\left\langle n_{a}n_{b}{\displaystyle \frac{|\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}|^{2}}{B^{2}}}\right\rangle M_{ab}^{01}\left({\displaystyle \frac{T_{a}}{Z_{a}}}{\displaystyle \frac{\text{d}\ln \unicode[STIX]{x1D702}_{a}}{\text{d}\unicode[STIX]{x1D713}}}-{\displaystyle \frac{T_{b}}{Z_{b}}}{\displaystyle \frac{\text{d}\ln \unicode[STIX]{x1D702}_{b}}{\text{d}\unicode[STIX]{x1D713}}}\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\,\left\langle n_{a}n_{b}{\displaystyle \frac{|\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}|^{2}}{B^{2}}}e\tilde{\unicode[STIX]{x1D6F7}}\right\rangle M_{ab}^{01}\left({\displaystyle \frac{\text{d}\ln T_{a}}{\text{d}\unicode[STIX]{x1D713}}}-{\displaystyle \frac{\text{d}\ln T_{b}}{\text{d}\unicode[STIX]{x1D713}}}\right)\nonumber\\ \displaystyle & & \displaystyle \left.+\left\langle n_{a}n_{b}{\displaystyle \frac{|\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}|^{2}}{B^{2}}}\right\rangle \left[(M_{ab}^{01}-M_{ab}^{11}){\displaystyle \frac{T_{a}}{Z_{a}}}{\displaystyle \frac{\text{d}\ln T_{a}}{\text{d}\unicode[STIX]{x1D713}}}-(M_{ab}^{01}+N_{ab}^{11}){\displaystyle \frac{T_{b}}{Z_{b}}}{\displaystyle \frac{\text{d}\ln T_{b}}{\text{d}\unicode[STIX]{x1D713}}}\right]\right\},\end{eqnarray}$$
where
![]() $M_{ab}^{jk}$
are the Braginskii matrix elements (Braginskii Reference Braginskii1958), defined in appendix A, using the same notation as Helander & Sigmar (Reference Helander and Sigmar2005); the collision time
$M_{ab}^{jk}$
are the Braginskii matrix elements (Braginskii Reference Braginskii1958), defined in appendix A, using the same notation as Helander & Sigmar (Reference Helander and Sigmar2005); the collision time
![]() $\unicode[STIX]{x1D70F}_{ab}$
is defined as
$\unicode[STIX]{x1D70F}_{ab}$
is defined as
where
![]() $\text{ln}\,\unicode[STIX]{x1D6EC}$
is the Coulomb logarithm, and
$\text{ln}\,\unicode[STIX]{x1D6EC}$
is the Coulomb logarithm, and
![]() $\unicode[STIX]{x1D716}_{0}$
the vacuum permittivity. These expressions are valid for all collisionalities. In (3.9) and (3.10), the effect of
$\unicode[STIX]{x1D716}_{0}$
the vacuum permittivity. These expressions are valid for all collisionalities. In (3.9) and (3.10), the effect of
![]() $\tilde{\unicode[STIX]{x1D6F7}}$
is to induce a weighting over the flux surface due to the flux-surface variation of
$\tilde{\unicode[STIX]{x1D6F7}}$
is to induce a weighting over the flux surface due to the flux-surface variation of
![]() $n_{a}$
and its radial gradient. Note that the radial electric field (from
$n_{a}$
and its radial gradient. Note that the radial electric field (from
![]() $\langle \unicode[STIX]{x1D6F7}\rangle$
and
$\langle \unicode[STIX]{x1D6F7}\rangle$
and
![]() $\tilde{\unicode[STIX]{x1D6F7}}$
) does not contribute in the above expression, even when
$\tilde{\unicode[STIX]{x1D6F7}}$
) does not contribute in the above expression, even when
![]() $\text{d}\ln \unicode[STIX]{x1D702}/\text{d}\unicode[STIX]{x1D713}$
is expressed in terms of (3.7).
$\text{d}\ln \unicode[STIX]{x1D702}/\text{d}\unicode[STIX]{x1D713}$
is expressed in terms of (3.7).
In (3.9)–(3.10), the
![]() $|\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}|^{2}$
factors correspond to the
$|\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}|^{2}$
factors correspond to the
![]() $j_{\bot }$
factor in (2.1), while the
$j_{\bot }$
factor in (2.1), while the
![]() $j_{\Vert }$
factor in (2.1) arises due to the neoclassical transport (Braun & Helander Reference Braun and Helander2010; Helander et al.
Reference Helander, Newton, Mollén and Smith2017). In the following section, we will evaluate the above expression for example magnetic configurations.
$j_{\Vert }$
factor in (2.1) arises due to the neoclassical transport (Braun & Helander Reference Braun and Helander2010; Helander et al.
Reference Helander, Newton, Mollén and Smith2017). In the following section, we will evaluate the above expression for example magnetic configurations.
4 Comparison to neoclassical calculations
In this section, we will compare the classical transport from (3.9) to the neoclassical transport calculated with the drift-kinetic solver Sfincs. Unlike analytical calculations of the neoclassical transport (Buller et al. Reference Buller, Smith, Helander, Mollén, Newton and Pusztai2018; Calvo et al. Reference Calvo, Parra, Velasco, Alonso and Na2018), this procedure is not limited to a specific collisionality regime, which will let us assess the importance of classical transport for any collisionality.
For this study, we will look at two stellarator configurations, where the neoclassical transport coefficients have been calculated across a wide range of collisionalities. Specifically, we will look at a simulated W7-X standard configuration case at the radial location
![]() $r_{N}=0.88$
, with
$r_{N}=0.88$
, with
![]() $T=1~\text{keV}$
and impurity parameters
$T=1~\text{keV}$
and impurity parameters
![]() $Z=6$
,
$Z=6$
,
![]() $Z_{\text{eff}}=2.0$
, studied by Mollén et al. (Reference Mollén, Landreman, Smith, Braun and Helander2015). The normalized radius is defined as
$Z_{\text{eff}}=2.0$
, studied by Mollén et al. (Reference Mollén, Landreman, Smith, Braun and Helander2015). The normalized radius is defined as
![]() $r_{N}=\sqrt{\unicode[STIX]{x1D713}_{\text{t}}/\unicode[STIX]{x1D713}_{\text{t},\text{LCFS}}}$
, with
$r_{N}=\sqrt{\unicode[STIX]{x1D713}_{\text{t}}/\unicode[STIX]{x1D713}_{\text{t},\text{LCFS}}}$
, with
![]() $\unicode[STIX]{x1D713}_{t}$
the toroidal flux and
$\unicode[STIX]{x1D713}_{t}$
the toroidal flux and
![]() $\unicode[STIX]{x1D713}_{\text{t},\text{LCFS}}$
its value at the last-closed flux surface. Since W7-X has been optimized for a low parallel current, and the standard configuration has low neoclassical transport compared to other configurations, we here expect the classical transport to dominate at high collisionality, as indicated at the end of § 2. In addition, we will look at a scenario based on an impurity hole plasma (
$\unicode[STIX]{x1D713}_{\text{t},\text{LCFS}}$
its value at the last-closed flux surface. Since W7-X has been optimized for a low parallel current, and the standard configuration has low neoclassical transport compared to other configurations, we here expect the classical transport to dominate at high collisionality, as indicated at the end of § 2. In addition, we will look at a scenario based on an impurity hole plasma (
![]() $\#113208$
,
$\#113208$
,
![]() $t=4.64~\text{s}$
,
$t=4.64~\text{s}$
,
![]() $r_{N}=0.6$
,
$r_{N}=0.6$
,
![]() $T=3.2~\text{keV}$
) of the Large Helical Device (LHD), where we replaced the mixture of helium and carbon impurities with purely carbon (
$T=3.2~\text{keV}$
) of the Large Helical Device (LHD), where we replaced the mixture of helium and carbon impurities with purely carbon (
![]() $Z_{\text{eff}}=3.44$
) for the sake of comparison. This magnetic configuration has been investigated in several studies, using both neoclassical (Velasco et al.
Reference Velasco, Calvo, Satake, Alonso, Nunami, Yokoyama, Sato, Estrada, Fontdecaba and Liniers2017; Mollén et al.
Reference Mollén, Landreman, Smith, García-Regaña and Nunami2018) and turbulence codes (Nunami et al.
Reference Nunami, Sugama, Velasco, Yokoyama, Sato, Nakata and Satake2016).
$Z_{\text{eff}}=3.44$
) for the sake of comparison. This magnetic configuration has been investigated in several studies, using both neoclassical (Velasco et al.
Reference Velasco, Calvo, Satake, Alonso, Nunami, Yokoyama, Sato, Estrada, Fontdecaba and Liniers2017; Mollén et al.
Reference Mollén, Landreman, Smith, García-Regaña and Nunami2018) and turbulence codes (Nunami et al.
Reference Nunami, Sugama, Velasco, Yokoyama, Sato, Nakata and Satake2016).
Effects of
![]() $\tilde{\unicode[STIX]{x1D6F7}}$
and the radial electric field are not included in this demonstration (they are zero in the simulations), as this would make the drift-kinetic equation nonlinear, and add the complexity of finding the ambipolar electric field at each step. These effects are not expected to strongly affect the classical transport, which is independent of the radial electric field, and typically not as sensitive to
$\tilde{\unicode[STIX]{x1D6F7}}$
and the radial electric field are not included in this demonstration (they are zero in the simulations), as this would make the drift-kinetic equation nonlinear, and add the complexity of finding the ambipolar electric field at each step. These effects are not expected to strongly affect the classical transport, which is independent of the radial electric field, and typically not as sensitive to
![]() $\tilde{\unicode[STIX]{x1D6F7}}$
as the neoclassical transport (Buller et al.
Reference Buller, Smith, Helander, Mollén, Newton and Pusztai2018). The neoclassical transport can be both enhanced or reduced by these effects, which thus would affect the relative importance of classical transport. These effects will be touched upon in § 5. As
$\tilde{\unicode[STIX]{x1D6F7}}$
as the neoclassical transport (Buller et al.
Reference Buller, Smith, Helander, Mollén, Newton and Pusztai2018). The neoclassical transport can be both enhanced or reduced by these effects, which thus would affect the relative importance of classical transport. These effects will be touched upon in § 5. As
![]() $\tilde{\unicode[STIX]{x1D6F7}}=0$
in this section, the density is a flux function, and
$\tilde{\unicode[STIX]{x1D6F7}}=0$
in this section, the density is a flux function, and
![]() $\unicode[STIX]{x1D702}_{a}=n_{a}$
.
$\unicode[STIX]{x1D702}_{a}=n_{a}$
.
We scan the collisionality by artificially scaling the collision frequency. For each point in the collisionality scan, we calculate the neoclassical and classical transport coefficients of the hydrogen bulk ion and the carbon impurity. The transport coefficients for the (neo)classical fluxes are defined such that
where
![]() $a=i,z$
for ions and impurities. We have neglected the effects of electron collisions on the ion fluxes due to the small electron-to-ion mass ratio, and assumed that the bulk and impurity ions have the same temperature
$a=i,z$
for ions and impurities. We have neglected the effects of electron collisions on the ion fluxes due to the small electron-to-ion mass ratio, and assumed that the bulk and impurity ions have the same temperature
![]() $T\equiv T_{i}=T_{z}$
.
$T\equiv T_{i}=T_{z}$
.
The results of the collisionality scan are shown in figure 1, with the collisionality defined as
where
![]() $B_{00}$
,
$B_{00}$
,
![]() $G$
and
$G$
and
![]() $I$
are related to the Boozer representation of the magnetic field (see, for example, Mollén et al. (Reference Mollén, Landreman, Smith, García-Regaña and Nunami2018)) and
$I$
are related to the Boozer representation of the magnetic field (see, for example, Mollén et al. (Reference Mollén, Landreman, Smith, García-Regaña and Nunami2018)) and
![]() $\unicode[STIX]{x1D704}$
is the rotational transform. As seen in the left panels of figure 1, the impurity transport coefficients in the W7-X geometry are dominantly classical already for
$\unicode[STIX]{x1D704}$
is the rotational transform. As seen in the left panels of figure 1, the impurity transport coefficients in the W7-X geometry are dominantly classical already for
![]() $\hat{\unicode[STIX]{x1D708}}_{CC}\gtrsim 1$
. The cross-species contributions are dominantly classical at even lower collisionality,
$\hat{\unicode[STIX]{x1D708}}_{CC}\gtrsim 1$
. The cross-species contributions are dominantly classical at even lower collisionality,
![]() $\hat{\unicode[STIX]{x1D708}}_{CC}\gtrsim 0.1$
, for both the bulk and the impurity ions. On the other hand, in LHD – which has not been optimized for low
$\hat{\unicode[STIX]{x1D708}}_{CC}\gtrsim 0.1$
, for both the bulk and the impurity ions. On the other hand, in LHD – which has not been optimized for low
![]() $|j_{\Vert }|/|\boldsymbol{j}_{\bot }|$
– the classical transport for both species at most collisionalities is at least an order of magnitude smaller than the neoclassical transport. An exception to this is the
$|j_{\Vert }|/|\boldsymbol{j}_{\bot }|$
– the classical transport for both species at most collisionalities is at least an order of magnitude smaller than the neoclassical transport. An exception to this is the
![]() $D_{a,T}$
coefficient, where the classical transport becomes comparable to or greater than the neoclassical transport at very high collisionalities (
$D_{a,T}$
coefficient, where the classical transport becomes comparable to or greater than the neoclassical transport at very high collisionalities (
![]() $\hat{\unicode[STIX]{x1D708}}_{CC}\gtrsim 100$
). Another exception occurs in the collisionality range
$\hat{\unicode[STIX]{x1D708}}_{CC}\gtrsim 100$
). Another exception occurs in the collisionality range
![]() $\unicode[STIX]{x1D708}_{CC}\sim [0.1,1]$
, where the cross-species neoclassical
$\unicode[STIX]{x1D708}_{CC}\sim [0.1,1]$
, where the cross-species neoclassical
![]() $D_{z,ni}$
and
$D_{z,ni}$
and
![]() $D_{i,nz}$
coefficients transition between different signs.
$D_{i,nz}$
coefficients transition between different signs.
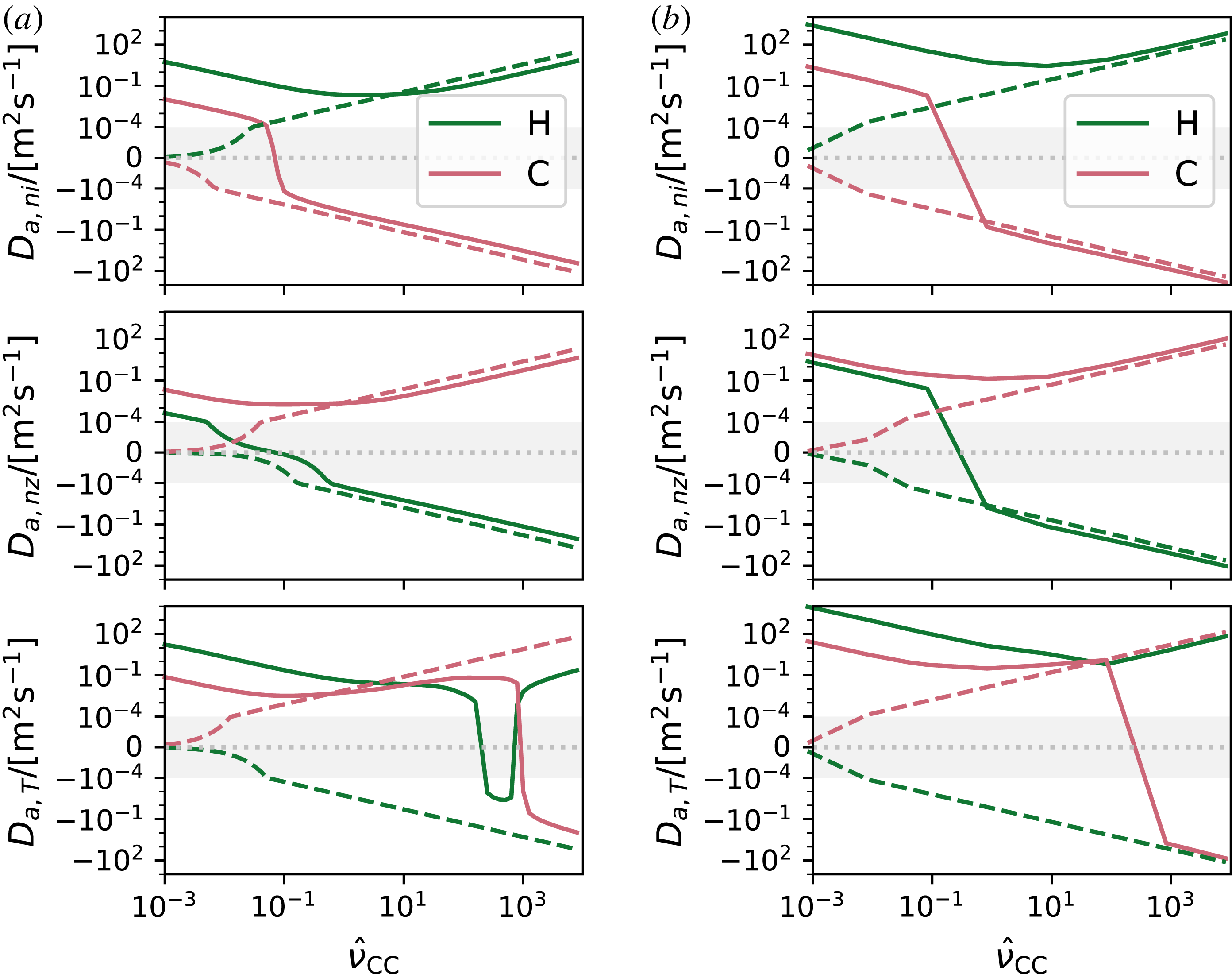
Figure 1. The neoclassical (——) and classical (- - -) transport coefficients as defined in (4.1), plotted against the impurity–impurity collisionality. (a) W7-X standard case. (b) LHD impurity–hole case. The classical coefficients were calculated using (3.9), while the neoclassical coefficients were calculated using Sfincs. Note the symmetric logarithmic scale of the
![]() $y$
-axis; the shaded region has a linear
$y$
-axis; the shaded region has a linear
![]() $y$
-axis scale.
$y$
-axis scale.
5 Discussion
We have seen that the neoclassical and classical transport coefficients can be comparable in a W7-X standard configuration, even at modest impurity collisionality (
![]() $\hat{\unicode[STIX]{x1D708}}_{\text{CC}}\gtrsim 0.1$
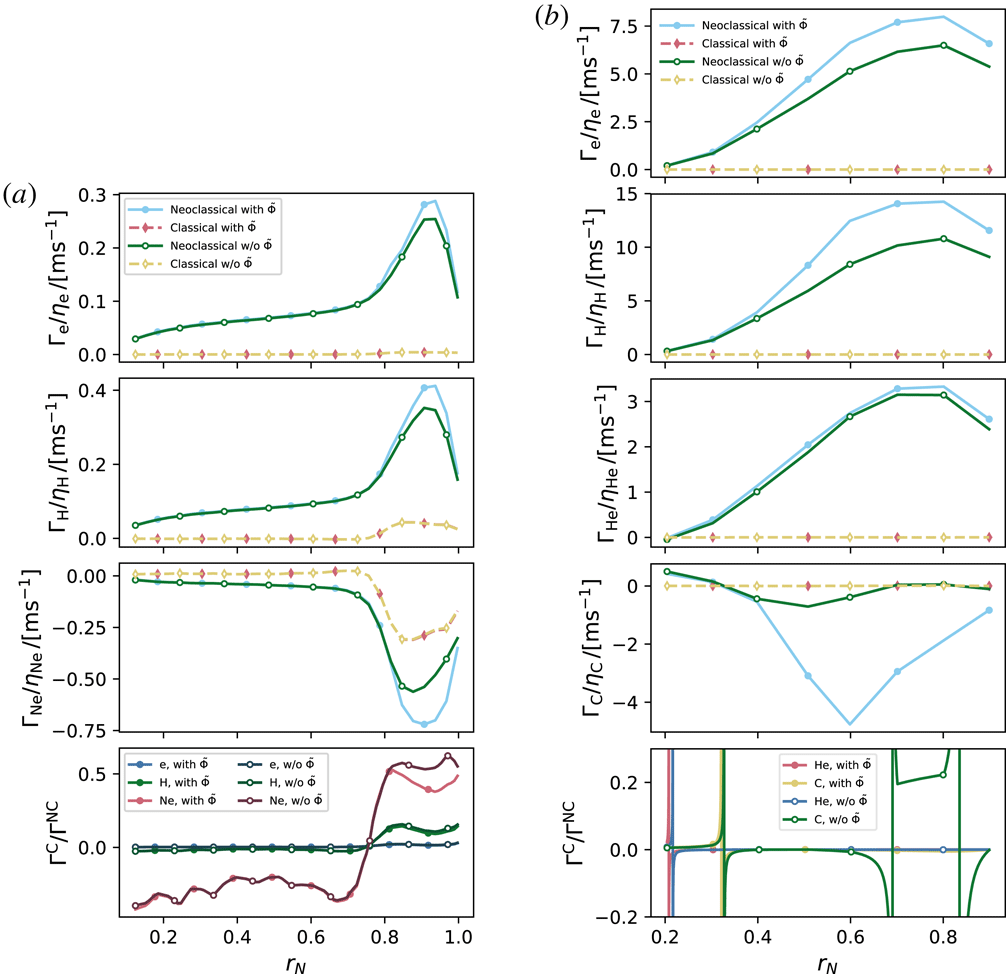
–1), although the previously discussed simulations do not include effects of electrostatic potential variation within and across flux surfaces and collisions with electrons. To demonstrate the relative importance of neoclassical and classical transport in realistic scenarios with these effects included, we consider two cases in which the full neoclassical behaviour has previously been analysed by Mollén et al. (Reference Mollén, Landreman, Smith, García-Regaña and Nunami2018): a simulated neutral-beam heated high-mirror W7-X scenario with inward electric field and neon impurities, and the impurity hole LHD case of the previous section with an additional helium impurity.
$\hat{\unicode[STIX]{x1D708}}_{\text{CC}}\gtrsim 0.1$
–1), although the previously discussed simulations do not include effects of electrostatic potential variation within and across flux surfaces and collisions with electrons. To demonstrate the relative importance of neoclassical and classical transport in realistic scenarios with these effects included, we consider two cases in which the full neoclassical behaviour has previously been analysed by Mollén et al. (Reference Mollén, Landreman, Smith, García-Regaña and Nunami2018): a simulated neutral-beam heated high-mirror W7-X scenario with inward electric field and neon impurities, and the impurity hole LHD case of the previous section with an additional helium impurity.
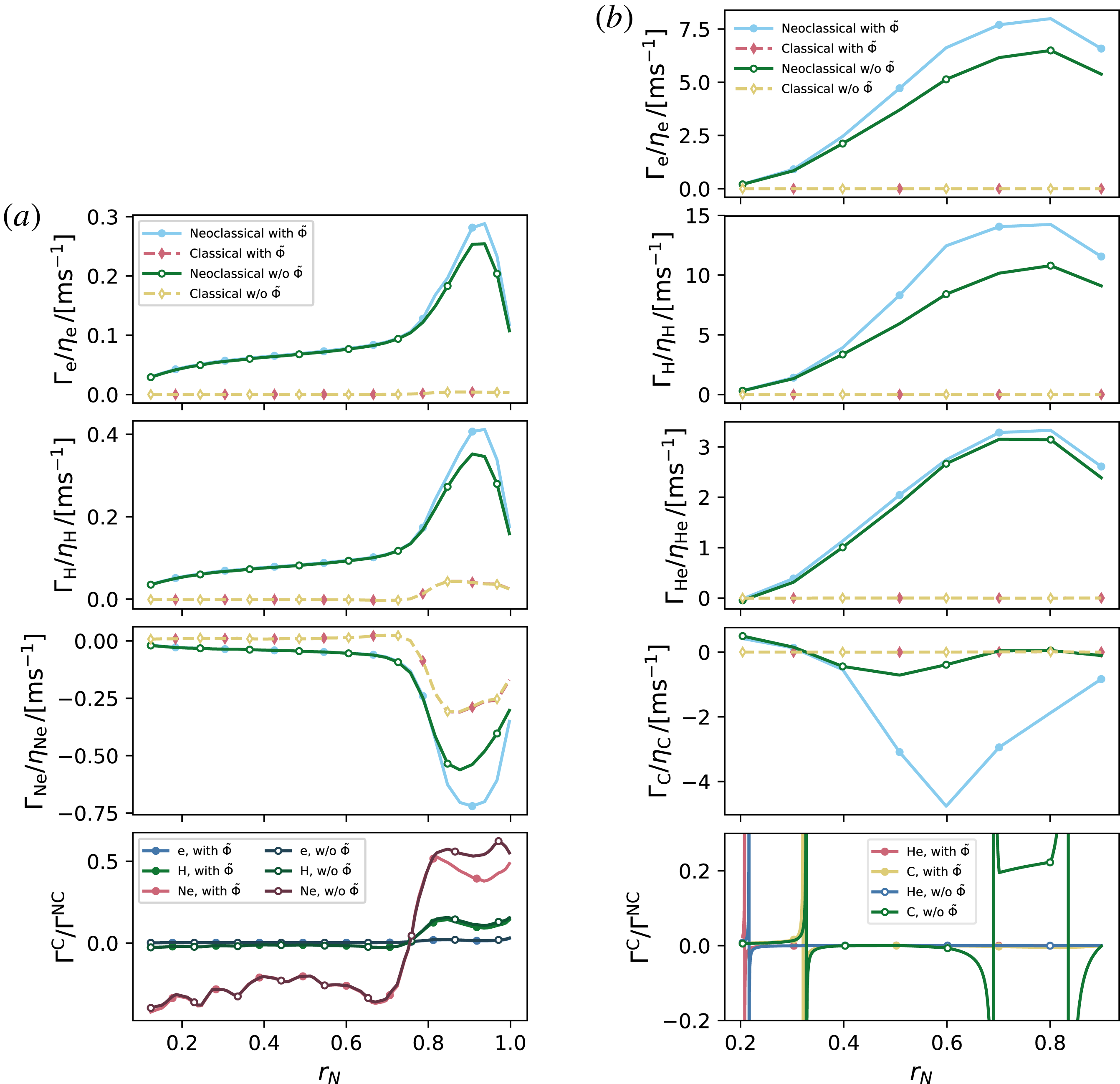
Figure 2. Neoclassical (——) and classical (- - -) fluxes normalized to pseudo-densities for different species in W7-X (a) and LHD (b) as functions of the normalized radius
![]() $r_{N}$
. Filled (open) symbols show the flux with (without) the effect of
$r_{N}$
. Filled (open) symbols show the flux with (without) the effect of
![]() $\tilde{\unicode[STIX]{x1D6F7}}$
included. The lowest panels show the ratio of the classical and neoclassical transport; note that this quantity diverges at radii where the neoclassical flux crosses zero.
$\tilde{\unicode[STIX]{x1D6F7}}$
included. The lowest panels show the ratio of the classical and neoclassical transport; note that this quantity diverges at radii where the neoclassical flux crosses zero.
The classical and neoclassical fluxes are shown in figure 2 (left panels, W7X; right panels, LHD). We note that in the W7-X case, the classical to neoclassical neon flux ratio is around
![]() $0.5$
in magnitude at most radii, and its sensitivity to a finite
$0.5$
in magnitude at most radii, and its sensitivity to a finite
![]() $\tilde{\unicode[STIX]{x1D6F7}}$
is weak. This is consistent with neon being the only collisional impurity in this discharge (with
$\tilde{\unicode[STIX]{x1D6F7}}$
is weak. This is consistent with neon being the only collisional impurity in this discharge (with
![]() $\hat{\unicode[STIX]{x1D708}}_{\text{NeNe}}\sim [0.5,2.5]$
).
$\hat{\unicode[STIX]{x1D708}}_{\text{NeNe}}\sim [0.5,2.5]$
).
In the LHD case, the classical flux is generally small, although the classical to neoclassical flux ratio for carbon and helium diverges at discrete points, where the neoclassical flux crosses zero. Additionally, for
![]() $\tilde{\unicode[STIX]{x1D6F7}}=0$
, there is a radial range (
$\tilde{\unicode[STIX]{x1D6F7}}=0$
, there is a radial range (
![]() $0.6\lesssim r_{N}\lesssim 0.8$
), with small outward neoclassical carbon flux, where the neoclassical flux is only 5 times as large as the classical. When the effect of
$0.6\lesssim r_{N}\lesssim 0.8$
), with small outward neoclassical carbon flux, where the neoclassical flux is only 5 times as large as the classical. When the effect of
![]() $\tilde{\unicode[STIX]{x1D6F7}}$
is included, there is a large increase in the neoclassical carbon flux for
$\tilde{\unicode[STIX]{x1D6F7}}$
is included, there is a large increase in the neoclassical carbon flux for
![]() $r_{N}\gtrsim 0.4$
, with the result that the classical-to-neoclassical flux ratio remains small for these radii.
$r_{N}\gtrsim 0.4$
, with the result that the classical-to-neoclassical flux ratio remains small for these radii.
As all species in the LHD case are in a low-collisionality regime, it is unlikely that the low neoclassical transport for
![]() $\tilde{\unicode[STIX]{x1D6F7}}=0$
is due to small neoclassical transport coefficients, when compared to the classical coefficients. Rather, it may be that the contributions from the different neoclassical transport coefficients cancel out approximately. Including potential variations both changes the individual transport coefficient and somewhat reduces the ambipolar radial electric field in this case, both of which could affect this cancellation.
$\tilde{\unicode[STIX]{x1D6F7}}=0$
is due to small neoclassical transport coefficients, when compared to the classical coefficients. Rather, it may be that the contributions from the different neoclassical transport coefficients cancel out approximately. Including potential variations both changes the individual transport coefficient and somewhat reduces the ambipolar radial electric field in this case, both of which could affect this cancellation.
The classical fluxes are comparable to the neoclassical fluxes in W7-X, and should not generally be neglected in an analysis of the collisional transport. Based on this conclusion, we have implemented the classical fluxes (3.9)–(3.10) as a post-processing step to the neoclassical codes Sfincs and Dkes; see the supplementary material, available at https://doi.org/10.1017/S002237781900045X, for an example implementation in python.
As a final remark, we note that since the neoclassical transport in W7-X is sufficiently low to be comparable to the classical, the transport due to micro-turbulence can become relatively more important. It may thus be necessary to consider the effect of turbulence on stellarator impurity transport in the future, which is often excluded due to the computational expense of simulating turbulence in stellarator geometry (Nunami, Watanabe & Sugama Reference Nunami, Watanabe and Sugama2013). Recent experimental studies by Langenberg et al. (Reference Langenberg, Warmer, Fuchert, Marchuk, Dinklage, Wegner, Alonso, Bozhenkov, Brunner and Burhenn2018) and Geiger et al. (Reference Geiger, Wegner, Beidler, Burhenn, Buttenschön, Dux, Langenberg, Pablant, Pütterich and Turkin2019) already point strongly in that direction.
Acknowledgements
S.B. and I.P. were supported by the International Career Grant of Vetenskapsrådet (Dnr. 330-2014-6313) and I.P. by Marie Sklodowska Curie Actions, Cofund, Project INCA 600398. S.B.’s visit to Greifswald was supported by Chalmersska forskningsfonden. This work has been carried out within the framework of the EUROfusion Consortium and has received funding from the Euratom research and training programme 2014-2018 and 2019-2020 under grant agreement No 633053. The views and opinions expressed herein do not necessarily reflect those of the European Commission. The authors would like to thank the LHD experiment group and the technical staff of LHD for their support of this work. The authors are grateful to M. Nunami for help with accessing the LHD data.
Supplementary material
Supplementary material is available at https://doi.org/10.1017/S002237781900045X.
Appendix A. Braginskii matrix elements
The Braginskii matrix elements are defined by
where
![]() $v_{2}$
is any Cartesian velocity component,
$v_{2}$
is any Cartesian velocity component,
![]() $f_{a0}$
is a Maxwellian,
$f_{a0}$
is a Maxwellian,
![]() $x_{a}=v/\sqrt{2T_{a}/m_{a}}$
,
$x_{a}=v/\sqrt{2T_{a}/m_{a}}$
,
![]() $L_{k}^{(3/2)}$
are Sonine polynomials, where the polynomials relevant to classical particle and heat transport are
$L_{k}^{(3/2)}$
are Sonine polynomials, where the polynomials relevant to classical particle and heat transport are
The corresponding relevant matrix elements are
 $$\begin{eqnarray}\displaystyle & \displaystyle M_{ab}^{00}=-{\displaystyle \frac{\left(1+{\displaystyle \frac{m_{a}}{m_{b}}}\right)\left(1+{\displaystyle \frac{m_{a}T_{b}}{m_{b}T_{a}}}\right)}{\left(1+{\displaystyle \frac{m_{a}T_{b}}{m_{b}T_{a}}}\right)^{5/2}}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle M_{ab}^{00}=-{\displaystyle \frac{\left(1+{\displaystyle \frac{m_{a}}{m_{b}}}\right)\left(1+{\displaystyle \frac{m_{a}T_{b}}{m_{b}T_{a}}}\right)}{\left(1+{\displaystyle \frac{m_{a}T_{b}}{m_{b}T_{a}}}\right)^{5/2}}}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle M_{ab}^{01}=-{\displaystyle \frac{3}{2}}{\displaystyle \frac{1+{\displaystyle \frac{m_{a}}{m_{b}}}}{\left(1+{\displaystyle \frac{m_{a}T_{b}}{m_{b}T_{a}}}\right)^{5/2}}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle M_{ab}^{01}=-{\displaystyle \frac{3}{2}}{\displaystyle \frac{1+{\displaystyle \frac{m_{a}}{m_{b}}}}{\left(1+{\displaystyle \frac{m_{a}T_{b}}{m_{b}T_{a}}}\right)^{5/2}}}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle M_{ab}^{11}=-{\displaystyle \frac{{\displaystyle \frac{13}{4}}+4{\displaystyle \frac{m_{a}T_{b}}{m_{b}T_{a}}}+{\displaystyle \frac{15}{2}}\left({\displaystyle \frac{m_{a}T_{b}}{m_{b}T_{a}}}\right)^{2}}{\left(1+{\displaystyle \frac{m_{a}T_{b}}{m_{b}T_{a}}}\right)^{5/2}}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle M_{ab}^{11}=-{\displaystyle \frac{{\displaystyle \frac{13}{4}}+4{\displaystyle \frac{m_{a}T_{b}}{m_{b}T_{a}}}+{\displaystyle \frac{15}{2}}\left({\displaystyle \frac{m_{a}T_{b}}{m_{b}T_{a}}}\right)^{2}}{\left(1+{\displaystyle \frac{m_{a}T_{b}}{m_{b}T_{a}}}\right)^{5/2}}}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle N_{ab}^{11}={\displaystyle \frac{27}{4}}{\displaystyle \frac{{\displaystyle \frac{m_{a}}{m_{b}}}}{\left(1+{\displaystyle \frac{m_{a}T_{b}}{m_{b}T_{a}}}\right)^{5/2}}}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle N_{ab}^{11}={\displaystyle \frac{27}{4}}{\displaystyle \frac{{\displaystyle \frac{m_{a}}{m_{b}}}}{\left(1+{\displaystyle \frac{m_{a}T_{b}}{m_{b}T_{a}}}\right)^{5/2}}}. & \displaystyle\end{eqnarray}$$