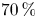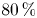1 Introduction
Plasma beat-wave acceleration (PBWA), first proposed by Tajima & Dawson (Reference Tajima and Dawson1979), is based on driving relativistic plasma waves by the ponderomotive force of the beat wave of two – typically picosecond long – laser pulses. Recently, there has been a renewed interest in the PBWA scheme, as an alternative to the prevailing laser wakefield acceleration (LWFA) scheme driven by femtosecond pulses (Leemans et al. Reference Leemans, Nagler, Gonsalves, Tóth, Nakamura, Geddes, Esarey, Schroeder and Hooker2006; Ke et al. Reference Ke, Feng, Wang, Qin, Yu, Wu, Chen, Qi, Zhang and Xu2021; Chen et al. Reference Chen, Maslarova, Wang, Lee, Horný and Umstadter2022; Oubrerie et al. Reference Oubrerie, Leblanc, Kononenko, Lahaye, Andriyash, Gautier, Goddet, Martelli, Tafzi and Ta Phuoc2022; Zhu et al. Reference Zhu, Li, Liu, Li, Bi, Ge, Deng, Zhang, Cui and Lu2023), as it allows for efficient acceleration over a wider range of plasma and laser parameters. For instance, the PBWA can operate at relaxed requirements on laser diffraction (Ponomareva & Shevchenko Reference Ponomareva and Shevchenko2023), allows electron acceleration at near-critical densities (Barraza-Valdez et al. Reference Barraza-Valdez, Tajima, Strickland and Roa2022), favours self-injection and it can be combined with a plasma channel to control the phase velocity of the plasma wave (Pukhov et al. Reference Pukhov, Andreev, Golovanov, Artemenko and Kostyukov2023). Our previous kinetic study of this scheme (Luo et al. Reference Luo, Riconda, Pusztai, Grassi, Wurtele and Fülöp2024) in one dimension demonstrates that autoresonance (Fajans & Friedland Reference Fajans and Friedland2001; Lindberg et al. Reference Lindberg, Charman, Wurtele and Friedland2004, Reference Lindberg, Charman, Wurtele, Friedland and Shadwick2006; Yaakobi et al. Reference Yaakobi, Friedland, Lindberg, Charman, Penn and Wurtele2008; Chapman et al. Reference Chapman, Hüller, Masson-Laborde, Heron, Pesme and Rozmus2012; Luo et al. Reference Luo, Hüller, Chen and Sheng2022a) can increase the plasma wave amplitude beyond the Rosenbluth–Liu (RL) limit (Rosenbluth & Liu Reference Rosenbluth and Liu1972), up to the wave-breaking limit, and it provides guidance to choose the laser and plasma parameters optimally. However, the desirable properties of autoresonant PBWA that survive the test of multi-dimensionality remain to be demonstrated.
In this paper, we employ the fully kinetic, two-dimensional (2-D) particle-in-cell (PIC) code Smilei (Derouillat et al. Reference Derouillat, Beck, Pérez, Vinci, Chiaramello, Grassi, Flé, Bouchard, Plotnikov and Aunai2018) to investigate multi-dimensional effects on autoresonantly driven large amplitude plasma waves. This extends previous work (Luo et al. Reference Luo, Riconda, Pusztai, Grassi, Wurtele and Fülöp2024), where we examined, again using Smilei, autoresonantly driven plasma wave excitation in one dimension under a wide range of plasma and laser parameters. In this paper, we restrict to a 2-D study of parameters that are representative in the one-dimensional (1-D) case of large amplitude plasma waves and electron self-trapping in the nonlinear regime. We are focused on the plasma dynamics, including both nonlinear and 2-D effects, in the presence of autoresonant excitation of a plasma wave. The autoresonant wakefield excitation process has not been previously studied in 2-D with a kinetic code.
In some recent work (Jakobsson, Hooker & Walczak Reference Jakobsson, Hooker and Walczak2021; van de Wetering, Hooker & Walczak Reference van de Wetering, Hooker and Walczak2024), a two-pulse scheme was studied, with a short initial relatively high-intensity drive laser, followed by a short gap, and then a trailing relatively low-intensity laser. Their scheme reaches the GeV-scale acceleration of an injected bunch over a distance of ${\sim }100\,{\rm mm}$![]() . In our simulations, both pulses are long and low power. We do not consider here the performance of the 2-D autoresonant beat wave with an injected bunch. At the high fields studied in our paper, beyond the RL limit and up to wave breaking, we see self-injection of electrons which are subsequently accelerated to ${\sim }200\,{\rm MeV}$
. In our simulations, both pulses are long and low power. We do not consider here the performance of the 2-D autoresonant beat wave with an injected bunch. At the high fields studied in our paper, beyond the RL limit and up to wave breaking, we see self-injection of electrons which are subsequently accelerated to ${\sim }200\,{\rm MeV}$![]() over ${\sim }3.5\,{\rm mm}$
over ${\sim }3.5\,{\rm mm}$![]() . In comparison with Jakobsson et al. (Reference Jakobsson, Hooker and Walczak2021) and van de Wetering et al. (Reference van de Wetering, Hooker and Walczak2024), the peak longitudinal electric field is higher here, because we have a higher density and we exceed the RL limit, up to the point of wave breaking.
. In comparison with Jakobsson et al. (Reference Jakobsson, Hooker and Walczak2021) and van de Wetering et al. (Reference van de Wetering, Hooker and Walczak2024), the peak longitudinal electric field is higher here, because we have a higher density and we exceed the RL limit, up to the point of wave breaking.
We find that in two dimensions, the acceleration of self-injected electrons remains comparable to that observed in one dimension, particularly in the early stages of the process. Further back in the process, after the peak plasma wave amplitude is reached, a variety of 2-D effects emerge (Forslund et al. Reference Forslund, Kindel, Mori, Joshi and Dawson1985) that reduce the wave amplitude and transverse coherence. These include parametric coupling (Luo et al. Reference Luo, Hüller, Chen and Sheng2022b; Sundström et al. Reference Sundström, Grech, Pusztai and Riconda2022), Weibel-like instabilities (Weibel Reference Weibel1959) and laser beam filamentation (Esarey, Schroeder & Leemans Reference Esarey, Schroeder and Leemans2009). These 2-D effects result in a reduced acceleration efficiency for self-injection of $70\,\%$![]() –$80\,\%$
–$80\,\%$![]() of that in the 1-D case.
of that in the 1-D case.
The rest of the paper is structured as follows. In § 2, we present 2-D kinetic simulations of autoresonant PBWA, with the simulation set-up explained in § 2.1, the wave excitation is examined in § 2.2 and accelerated electrons are discussed in § 2.3. Weak nonlinearities are examined in § 3.1, a Weibel-like instability is identified in § 3.2, and the strongly nonlinear regime and laser filamentation are studied in § 3.3. The results are summarized and discussed in § 4.
2 Autoresonant PBWA in two dimensions
We consider the most important characteristics of plasma beat-wave acceleration in two dimensions. We shall find that the early stages of the wave excitation and acceleration processes do not deviate significantly from corresponding one-dimensional results, while at later times, the acceleration in two dimensions starts to fall short of that in one dimension. The detailed analysis of these deviations will be addressed later in § 3.
2.1 Simulation set-up
In our 2-D investigation of the autoresonant PBWA, the two co-propagating laser beams are chosen to have parallel linear polarization and identical intensities. They have the shape of a sixth-order super-Gaussian temporal profile $\propto \exp [-(t/T_{\rm pulse})^6]$![]() , and $\propto \exp [-(y/w_0)^6]$
, and $\propto \exp [-(y/w_0)^6]$![]() in the transverse ($y$
in the transverse ($y$![]() ) direction, where the width of the laser beam $w_0$
) direction, where the width of the laser beam $w_0$![]() is set to be $2.4{\rm \pi} k_{\rm pe}^{-1}$
is set to be $2.4{\rm \pi} k_{\rm pe}^{-1}$![]() . Here, $k_{\rm pe}=\omega _{\rm pe}/c$
. Here, $k_{\rm pe}=\omega _{\rm pe}/c$![]() is the plasma wavenumber, $\omega _{\rm pe}=\sqrt {n_{e} e^2/\epsilon _0 m_e}$
is the plasma wavenumber, $\omega _{\rm pe}=\sqrt {n_{e} e^2/\epsilon _0 m_e}$![]() is the electron plasma frequency, $n_{e}$
is the electron plasma frequency, $n_{e}$![]() is the background electron density, $-e$
is the background electron density, $-e$![]() and $m_e$
and $m_e$![]() are the electron charge and mass, and $c$
are the electron charge and mass, and $c$![]() is the speed of light in vacuum.
is the speed of light in vacuum.
The laser and plasma parameters are chosen based on our previous 1-D study to reach the wave-breaking limit. Namely, the amplitudes of the two lasers (indicated by subscripts $1$![]() and $2$
and $2$![]() ) are $a_1=a_2= 0.2$
) are $a_1=a_2= 0.2$![]() in terms of the normalized vector potential $a = e A/m_ec$
in terms of the normalized vector potential $a = e A/m_ec$![]() . The ratio of homogeneous plasma density $n_{e}$
. The ratio of homogeneous plasma density $n_{e}$![]() and the critical density $n_{cr}$
and the critical density $n_{cr}$![]() is $0.0004$
is $0.0004$![]() , $n_{cr}=\omega _{1}^2m_e\epsilon _0/e^2$
, $n_{cr}=\omega _{1}^2m_e\epsilon _0/e^2$![]() is the critical density corresponding to a laser frequency $\omega _1$
is the critical density corresponding to a laser frequency $\omega _1$![]() , with $\omega _1$
, with $\omega _1$![]() the central frequency of the beam one (1). Before entering the homogeneous plasma, a linear density ramp with the gradient length $L_{\rm ramp}k_{\rm pe}=40{\rm \pi}$
the central frequency of the beam one (1). Before entering the homogeneous plasma, a linear density ramp with the gradient length $L_{\rm ramp}k_{\rm pe}=40{\rm \pi}$![]() is applied. A chirp rate $\alpha = -0.0014$
is applied. A chirp rate $\alpha = -0.0014$![]() is applied to the first laser beam, giving the frequency difference of the two laser beams $\Delta \omega =\omega _{\rm pe}[1+\alpha (t-t_0)\omega _{\rm pe}]$
is applied to the first laser beam, giving the frequency difference of the two laser beams $\Delta \omega =\omega _{\rm pe}[1+\alpha (t-t_0)\omega _{\rm pe}]$![]() . At time $t_0=22.5{\rm \pi} /\omega _{\rm pe}$
. At time $t_0=22.5{\rm \pi} /\omega _{\rm pe}$![]() , the frequency difference between the two lasers matches the nominal plasma frequency, $\Delta \omega =\omega _1-\omega _2=\omega _{\rm pe}$
, the frequency difference between the two lasers matches the nominal plasma frequency, $\Delta \omega =\omega _1-\omega _2=\omega _{\rm pe}$![]() . Here, the corresponding laser frequencies are $\omega _1/\omega _{\rm pe}=50$
. Here, the corresponding laser frequencies are $\omega _1/\omega _{\rm pe}=50$![]() and $\omega _2/\omega _{\rm pe}=49$
and $\omega _2/\omega _{\rm pe}=49$![]() . The laser duration $T_{\rm pulse}\omega _{\rm pe}=64{\rm \pi}$
. The laser duration $T_{\rm pulse}\omega _{\rm pe}=64{\rm \pi}$![]() is chosen to promote the autoresonant growth of the plasma wave until the wave-breaking limit. Further details on the choice of these parameters are given in Appendix A. The ions are set to be immobile, as they are not essential for the dynamics on the time scale of the laser pulse passing by (Mora et al. Reference Mora, Pesme, Héron, Laval and Silvestre1988). The longitudinal and transverse spatial resolutions are ${{\rm d} \kern0.7pt x}=0.008k_{\rm pe}^{-1}$
is chosen to promote the autoresonant growth of the plasma wave until the wave-breaking limit. Further details on the choice of these parameters are given in Appendix A. The ions are set to be immobile, as they are not essential for the dynamics on the time scale of the laser pulse passing by (Mora et al. Reference Mora, Pesme, Héron, Laval and Silvestre1988). The longitudinal and transverse spatial resolutions are ${{\rm d} \kern0.7pt x}=0.008k_{\rm pe}^{-1}$![]() and ${{\rm d} y}=2\,{\rm d}\kern0.7pt x$
and ${{\rm d} y}=2\,{\rm d}\kern0.7pt x$![]() , respectively. Table 1 shows the experimentally relevant parameters for a standard chirped pulse amplified $800\,{\rm nm}$
, respectively. Table 1 shows the experimentally relevant parameters for a standard chirped pulse amplified $800\,{\rm nm}$![]() Ti:sapphire laser.
Ti:sapphire laser.
Table 1. Simulation parameters.

2.2 Autoresonant plasma wave excitation in two dimensions
First, we consider the growth phase of the autoresonant beat-wave excitation, comparing 1-D and 2-D results. Figure 1 shows the longitudinal electrostatic field $E_L$![]() in the 2-D simulation at time $t \omega _{\rm pe}\approx 250$
in the 2-D simulation at time $t \omega _{\rm pe}\approx 250$![]() . The electric field is normalized to the Rosenbluth–Liu limit $E_{\rm RL}=(16a_1a_2/3)^{1/3}E_0$
. The electric field is normalized to the Rosenbluth–Liu limit $E_{\rm RL}=(16a_1a_2/3)^{1/3}E_0$![]() , where $E_0=m_ec\omega _{pe}/e$
, where $E_0=m_ec\omega _{pe}/e$![]() is the cold, non-relativistic wave-breaking field. The longitudinal coordinate is the co-moving position $\xi =\omega _{\rm pe}(x/c-t)$
is the cold, non-relativistic wave-breaking field. The longitudinal coordinate is the co-moving position $\xi =\omega _{\rm pe}(x/c-t)$![]() . Figures 1(a) and 1(b) correspond to simulations without chirp and with a chirp rate $\alpha =-0.0014$
. Figures 1(a) and 1(b) correspond to simulations without chirp and with a chirp rate $\alpha =-0.0014$![]() , respectively, that was deemed optimal for field enhancement with these parameters. The field enhancement with respect to the zero chirp case is evident in figure 1(a,b). The maximum value of the electric field in the chirp case is close to the cold, non-relativistic wave-breaking threshold $E_0$
, respectively, that was deemed optimal for field enhancement with these parameters. The field enhancement with respect to the zero chirp case is evident in figure 1(a,b). The maximum value of the electric field in the chirp case is close to the cold, non-relativistic wave-breaking threshold $E_0$![]() that takes the value $E_0/E_{\rm RL}\approx 1.67$
that takes the value $E_0/E_{\rm RL}\approx 1.67$![]() .
.

Figure 1. Longitudinal electric field of the plasma wave normalized to the RL field, $E_L / E_{\rm RL}$![]() , in the $2 \mathrm {D}$
, in the $2 \mathrm {D}$![]() simulations, evaluated at $t \omega _{\mathrm {pe}} \approx 250$
simulations, evaluated at $t \omega _{\mathrm {pe}} \approx 250$![]() . The duration of the laser pulses is $T_{\text {pulse}} \omega _{\text {pe}} \approx 64 {\rm \pi}$
. The duration of the laser pulses is $T_{\text {pulse}} \omega _{\text {pe}} \approx 64 {\rm \pi}$![]() . (a) No chirp. (b) With chirp rate $\alpha =-0.0014$
. (a) No chirp. (b) With chirp rate $\alpha =-0.0014$![]() . (c) Electric field at the symmetry axis ($y=0$
. (c) Electric field at the symmetry axis ($y=0$![]() ). The blue (red) line corresponds to simulations without (with) chirp in two dimensions. Corresponding 1-D simulation data are shown by the light-blue (grey) lines without (with) chirp. The black dashed line indicates the wave-breaking field.
). The blue (red) line corresponds to simulations without (with) chirp in two dimensions. Corresponding 1-D simulation data are shown by the light-blue (grey) lines without (with) chirp. The black dashed line indicates the wave-breaking field.
Notice that, as clearly visible in figure 1(a), for the case $\alpha =0$![]() , the plasma wave amplitude is larger off-axis than closer to the symmetry axis, in the region $\xi \approx 100$
, the plasma wave amplitude is larger off-axis than closer to the symmetry axis, in the region $\xi \approx 100$![]() –$150$
–$150$![]() . This is caused by the finite size of the laser field in the transverse direction and the related intensity variation. As a consequence, the growth and saturation time of the plasma wave excitation varies transversally. Specifically, the saturation time in the standard PBWA scheme is approximately $t_{\rm sa}\omega _{\rm pe}=3.68(\omega _{\rm pe}\tau _{r})^{4/7}(a_1a_2)^{-2/7}$
. This is caused by the finite size of the laser field in the transverse direction and the related intensity variation. As a consequence, the growth and saturation time of the plasma wave excitation varies transversally. Specifically, the saturation time in the standard PBWA scheme is approximately $t_{\rm sa}\omega _{\rm pe}=3.68(\omega _{\rm pe}\tau _{r})^{4/7}(a_1a_2)^{-2/7}$![]() (Forslund et al. Reference Forslund, Kindel, Mori, Joshi and Dawson1985), where $\tau _{r}$
(Forslund et al. Reference Forslund, Kindel, Mori, Joshi and Dawson1985), where $\tau _{r}$![]() is the rise-time of the laser beam's temporal profile, introduced in § 2.1, leading to slower saturation of the plasma wave off-axis. Eventually, the RL limit is also reached at the off-axis regions, as visible in the plot.
is the rise-time of the laser beam's temporal profile, introduced in § 2.1, leading to slower saturation of the plasma wave off-axis. Eventually, the RL limit is also reached at the off-axis regions, as visible in the plot.
Figure 1(c) shows the electric field variation along the symmetry axis, i.e. $E_L(\xi, y=0)$![]() . The blue (red) line corresponds to the case without (with) chirp in two dimensions. For reference, we also present the 1-D simulation results, shown by the light-blue (grey) line without (with) chirp. The no-chirp results in one dimension and two dimensions overlap, and show that the RL value is indeed the limit of the achieved electric field; the maximum of the blue curves is at $E_L/E_{RL}=1$
. The blue (red) line corresponds to the case without (with) chirp in two dimensions. For reference, we also present the 1-D simulation results, shown by the light-blue (grey) line without (with) chirp. The no-chirp results in one dimension and two dimensions overlap, and show that the RL value is indeed the limit of the achieved electric field; the maximum of the blue curves is at $E_L/E_{RL}=1$![]() . When the optimal chirp value of $\alpha =-0.0014$
. When the optimal chirp value of $\alpha =-0.0014$![]() is employed, the autoresonant growth of the plasma wave is achieved and $E_L/E_{RL}=1$
is employed, the autoresonant growth of the plasma wave is achieved and $E_L/E_{RL}=1$![]() is exceeded, but the overlap of the 2-D and 1-D results (red and grey, respectively) extends only for $\xi \gtrsim 125$
is exceeded, but the overlap of the 2-D and 1-D results (red and grey, respectively) extends only for $\xi \gtrsim 125$![]() . Below this value, the 2-D results start to deviate from the 1-D ones. The reasons for this are discussed in detail in § 3.
. Below this value, the 2-D results start to deviate from the 1-D ones. The reasons for this are discussed in detail in § 3.
2.3 Energetic electron dynamics
After concluding that autoresonant plasma wave excitation is possible in two dimensions, we will now turn to the electron acceleration aspect of the process. Figure 2(a,b) show the electron phase space in terms of the co-moving coordinate $\xi$![]() and the kinetic energy reached by the electrons $U_{{\rm kin}}$
and the kinetic energy reached by the electrons $U_{{\rm kin}}$![]() (the data are integrated over the transverse coordinate). Self-injected electrons can be effectively accelerated by the electric field structure of the plasma wave and, as expected, electrons can reach higher energies – in this case, $200\,{\rm eV}$
(the data are integrated over the transverse coordinate). Self-injected electrons can be effectively accelerated by the electric field structure of the plasma wave and, as expected, electrons can reach higher energies – in this case, $200\,{\rm eV}$![]() at $t\omega _{\rm pe}\approx 750$
at $t\omega _{\rm pe}\approx 750$![]() – when a finite chirp of $\alpha =-0.0014$
– when a finite chirp of $\alpha =-0.0014$![]() is employed, allowing for autoresonant field growth; compare figure 2(b) with figure 2(a), where $\alpha =0$
is employed, allowing for autoresonant field growth; compare figure 2(b) with figure 2(a), where $\alpha =0$![]() . Notice that in the chirped case, electrons are mainly accelerated in the region of $100< \xi < 150$
. Notice that in the chirped case, electrons are mainly accelerated in the region of $100< \xi < 150$![]() , while in the region of $50 < \xi < 100$
, while in the region of $50 < \xi < 100$![]() , we observe energetic particles but at lower energies. This was also observed in the analogous 1-D kinetic simulation (Luo et al. Reference Luo, Riconda, Pusztai, Grassi, Wurtele and Fülöp2024), and can be understood in the following way. Because of autoresonance, the plasma wake field grows with decreasing $\xi$
, we observe energetic particles but at lower energies. This was also observed in the analogous 1-D kinetic simulation (Luo et al. Reference Luo, Riconda, Pusztai, Grassi, Wurtele and Fülöp2024), and can be understood in the following way. Because of autoresonance, the plasma wake field grows with decreasing $\xi$![]() . In the fluid model for the parameters chosen here (see Appendix A), it can become larger than $E_0$
. In the fluid model for the parameters chosen here (see Appendix A), it can become larger than $E_0$![]() , but in kinetic simulation, once it reaches $E_0$
, but in kinetic simulation, once it reaches $E_0$![]() , it starts to trap very efficiently particles that in turn stop the autoresonance. As a result, the field is highest in the range of $100< \xi < 150$
, it starts to trap very efficiently particles that in turn stop the autoresonance. As a result, the field is highest in the range of $100< \xi < 150$![]() with value slightly below $E_0$
with value slightly below $E_0$![]() . This is clearly visible in figure 1(c) for both the 2-D and 1-D chirped simulations (grey and red curves), the decrease of the field for $\xi < 100$
. This is clearly visible in figure 1(c) for both the 2-D and 1-D chirped simulations (grey and red curves), the decrease of the field for $\xi < 100$![]() being more pronounced in the 2-D case.
being more pronounced in the 2-D case.

Figure 2. Kinetic energy spectrum of electrons as a function of the co-moving coordinate $\xi$![]() , integrated over $y$
, integrated over $y$![]() , at $t \omega _{\mathrm {pe}} \approx 750$
, at $t \omega _{\mathrm {pe}} \approx 750$![]() are plotted (a) without chirp and (b) with chirp rate $\alpha =-0.0014$
are plotted (a) without chirp and (b) with chirp rate $\alpha =-0.0014$![]() . (c) Time traces of the highest electron kinetic energy for a variety of cases. The red ($\alpha =-0.0014$
. (c) Time traces of the highest electron kinetic energy for a variety of cases. The red ($\alpha =-0.0014$![]() ) line and blue ($\alpha =0$
) line and blue ($\alpha =0$![]() ) line are in two dimensions, the grey ($\alpha =-0.0014$
) line are in two dimensions, the grey ($\alpha =-0.0014$![]() ) line and light blue ($\alpha =0$
) line and light blue ($\alpha =0$![]() ) line are in one dimension. The black dashed and dotted lines indicate the kinetic energies of an electron that was accelerated by a constant electric fields at the wave-breaking ($E_0$
) line are in one dimension. The black dashed and dotted lines indicate the kinetic energies of an electron that was accelerated by a constant electric fields at the wave-breaking ($E_0$![]() ) and the RL limit ($E_{\rm RL}$
) and the RL limit ($E_{\rm RL}$![]() ). (d) Temporal evolution of the maximum electric field $E_{L, \max }$
). (d) Temporal evolution of the maximum electric field $E_{L, \max }$![]() is shown in magenta (right axis). If an electron was accelerated with this time-varying field, it would reach energies as shown by the green curve (left axis). For reference, the dashed and the red lines of panel (c) are repeated.
is shown in magenta (right axis). If an electron was accelerated with this time-varying field, it would reach energies as shown by the green curve (left axis). For reference, the dashed and the red lines of panel (c) are repeated.
We now focus on the region $\xi > 100$![]() . To assess the efficiency of the acceleration process, we track the kinetic energy of electrons reaching the highest energies (note that the acceleration starts at slightly different times in the various simulations). In figure 2(c), we compare the temporal evolution to estimate the acceleration efficiency corresponding to the acceleration of relativistic electrons by a constant electric field at the RL limit, $E_{\rm RL}$
. To assess the efficiency of the acceleration process, we track the kinetic energy of electrons reaching the highest energies (note that the acceleration starts at slightly different times in the various simulations). In figure 2(c), we compare the temporal evolution to estimate the acceleration efficiency corresponding to the acceleration of relativistic electrons by a constant electric field at the RL limit, $E_{\rm RL}$![]() (dotted line), and at the wave breaking value, $E_0$
(dotted line), and at the wave breaking value, $E_0$![]() (dashed line). As expected, we find that in the no-chirp cases, the kinetic energy mostly increases with a steepness dictated by the RL field limit. The 1-D simulation (light blue) stably accelerates at this rate up to the end of the considered time range, while we observe a reducing slope in two dimensions (dark blue). In the simulations with chirp, the electron energy initially increases closely following the wave-breaking field estimate. At later times, the slope changes slightly in one dimension and more significantly in the 2-D simulation. The 1-D and 2-D autoresonant results (grey and red line, respectively) quite closely follow each other up to $t\omega _{\rm pe}\approx 450$
(dashed line). As expected, we find that in the no-chirp cases, the kinetic energy mostly increases with a steepness dictated by the RL field limit. The 1-D simulation (light blue) stably accelerates at this rate up to the end of the considered time range, while we observe a reducing slope in two dimensions (dark blue). In the simulations with chirp, the electron energy initially increases closely following the wave-breaking field estimate. At later times, the slope changes slightly in one dimension and more significantly in the 2-D simulation. The 1-D and 2-D autoresonant results (grey and red line, respectively) quite closely follow each other up to $t\omega _{\rm pe}\approx 450$![]() , indicating a similar performance in the early stage of the acceleration.
, indicating a similar performance in the early stage of the acceleration.
Two reasons can be responsible for the difference between the autoresonant simulations and the estimate indicated by the dashed line. First, the maximum electric field might not be sustained at the constant level of $E_0$![]() and, second, the particles are not necessarily positioned to be optimally accelerated by the maximum electric field. We find that the first effect is the one mainly at play. Indeed, the kinetic energy of the most energetic particle from the simulations $U_{{\rm kin}, {\rm sim}}$
and, second, the particles are not necessarily positioned to be optimally accelerated by the maximum electric field. We find that the first effect is the one mainly at play. Indeed, the kinetic energy of the most energetic particle from the simulations $U_{{\rm kin}, {\rm sim}}$![]() as function of time should follow $U_{{\rm kin}, {\rm max}}$
as function of time should follow $U_{{\rm kin}, {\rm max}}$![]() defined by
defined by
where $E_{L, {\rm max}}$![]() is the maximum instantaneous electric field. In figure 2(d), the time evolution of $E_{L, {\rm max}}$
is the maximum instantaneous electric field. In figure 2(d), the time evolution of $E_{L, {\rm max}}$![]() is shown (magenta, right axis) along with the corresponding $U_{{\rm kin}, {\rm max}}$
is shown (magenta, right axis) along with the corresponding $U_{{\rm kin}, {\rm max}}$![]() (green) and $U_{{\rm kin}, {\rm sim}}$
(green) and $U_{{\rm kin}, {\rm sim}}$![]() (red). While $E_{L, {\rm max}}$
(red). While $E_{L, {\rm max}}$![]() remains in the vicinity of $E_0$
remains in the vicinity of $E_0$![]() , it is somewhat lower most of the time. Thus, the expected particle energy (green curve) departs downward from the theoretical upper bound (dashed). The actual electron energy (red curve), closely follows $U_{{\rm kin}, {\rm max}}$
, it is somewhat lower most of the time. Thus, the expected particle energy (green curve) departs downward from the theoretical upper bound (dashed). The actual electron energy (red curve), closely follows $U_{{\rm kin}, {\rm max}}$![]() until $t\omega _{\rm pe}\approx 400$
until $t\omega _{\rm pe}\approx 400$![]() , and then starts to deviate. This marks the beginning of a 2-D effect of the system that is strong enough to degrade the efficiency of acceleration. The responsible physical processes are to be detailed in § 3. We note that while the simulations presented here do not include a plasma–vacuum interface, additional simulations confirmed that, while the lower energy part of the electron distribution is pulled back by space charge forces at such a boundary, it has a negligible effect on the most energetic electron population.
, and then starts to deviate. This marks the beginning of a 2-D effect of the system that is strong enough to degrade the efficiency of acceleration. The responsible physical processes are to be detailed in § 3. We note that while the simulations presented here do not include a plasma–vacuum interface, additional simulations confirmed that, while the lower energy part of the electron distribution is pulled back by space charge forces at such a boundary, it has a negligible effect on the most energetic electron population.
Next, we consider the transverse distribution of high-energy particles. Figure 3 shows the transverse distribution of the most energetic electrons as a function of time. At each time, electrons in the uppermost $10\,\%$![]() of the currently spanned energy range are identified and their transverse distribution is colour plotted. The transverse integral of this colour plot is shown as a red curve (right axis). More specifically, defining the ‘high-energy’ electron density by $n_{\rm HE}(\xi,y,t)=\int _{0.9 U_{{\rm kin},{\rm max}}(t)}^{U_{{\rm kin},{\rm max}}(t)}f_e(U_{{\rm kin}},\xi,y,t)\,{\rm d}U_{{\rm kin}}$
of the currently spanned energy range are identified and their transverse distribution is colour plotted. The transverse integral of this colour plot is shown as a red curve (right axis). More specifically, defining the ‘high-energy’ electron density by $n_{\rm HE}(\xi,y,t)=\int _{0.9 U_{{\rm kin},{\rm max}}(t)}^{U_{{\rm kin},{\rm max}}(t)}f_e(U_{{\rm kin}},\xi,y,t)\,{\rm d}U_{{\rm kin}}$![]() , with the electron distribution function $f_e$
, with the electron distribution function $f_e$![]() , the colour plot shows $N_{\rm HE,y}(y,t)=\int \,{\rm d}\xi \, n_{\rm HE}(\xi,y,t)/n_e$
, the colour plot shows $N_{\rm HE,y}(y,t)=\int \,{\rm d}\xi \, n_{\rm HE}(\xi,y,t)/n_e$![]() , with the nominal electron density $n_e$
, with the nominal electron density $n_e$![]() , while the red line is $N_{\rm HE}(t)=\int \,{{\rm d} y} \,N_{\rm HE,y}(y,t)$
, while the red line is $N_{\rm HE}(t)=\int \,{{\rm d} y} \,N_{\rm HE,y}(y,t)$![]() ; note that here, the $y$
; note that here, the $y$![]() coordinate is normalized to $k_{\rm pe}^{-1}$
coordinate is normalized to $k_{\rm pe}^{-1}$![]() (similarly to $\xi$
(similarly to $\xi$![]() ). When interpreting this image, we must keep in mind that the considered energy range corresponds to continuously increasing energies, since $U_{{\rm kin},{\rm max}}=U_{{\rm kin},{\rm max}}(t)$
). When interpreting this image, we must keep in mind that the considered energy range corresponds to continuously increasing energies, since $U_{{\rm kin},{\rm max}}=U_{{\rm kin},{\rm max}}(t)$![]() . The highest number of energetic electrons is reached at $t\omega _{\rm pe}\simeq 400$
. The highest number of energetic electrons is reached at $t\omega _{\rm pe}\simeq 400$![]() , then it rapidly drops and stays around $20\,\%$
, then it rapidly drops and stays around $20\,\%$![]() . After this time, the electron energy keeps increasing but for a smaller population than at earlier times. Up to $t\omega _{\rm pe}=350$
. After this time, the electron energy keeps increasing but for a smaller population than at earlier times. Up to $t\omega _{\rm pe}=350$![]() , the fast electrons are mostly localized at the centre, while we observe a rapid widening of the transverse distribution after that. Even later, at approximately $t\omega _{\rm pe}=550$
, the fast electrons are mostly localized at the centre, while we observe a rapid widening of the transverse distribution after that. Even later, at approximately $t\omega _{\rm pe}=550$![]() , the most energetic electrons are found off-axis. Note that the highest energy electrons have been continuously accelerated, while those that fail to be accelerated to $90\,\%$
, the most energetic electrons are found off-axis. Note that the highest energy electrons have been continuously accelerated, while those that fail to be accelerated to $90\,\%$![]() of the highest energy are not present in this visualization.
of the highest energy are not present in this visualization.

Figure 3. Colour plot: the high-energy electron distribution ($N_{{\rm HE},y}(y,t)$![]() , integrating in $\xi$
, integrating in $\xi$![]() over the box length) is plotted. Red curve (right axis) shows $N_{{\rm HE}}(t)$
over the box length) is plotted. Red curve (right axis) shows $N_{{\rm HE}}(t)$![]() (integrating over the $y$
(integrating over the $y$![]() -axis). High-energy electrons are defined, for the plot, as those in the uppermost $10\,\%$
-axis). High-energy electrons are defined, for the plot, as those in the uppermost $10\,\%$![]() of the instantaneous energy range are considered. The two vertical dashed lines mark the times considered in figure 4, when the energetic electrons are localized on-axis and off-axis, respectively.
of the instantaneous energy range are considered. The two vertical dashed lines mark the times considered in figure 4, when the energetic electrons are localized on-axis and off-axis, respectively.
We now consider two snapshots, at the times indicated by the white dashed vertical lines in figure 3, and we show in figure 4 the logarithm of the relative number of energetic electrons as function of $\xi$![]() and $y$
and $y$![]() . At $t\omega _{\rm pe}=350$
. At $t\omega _{\rm pe}=350$![]() , shown in figure 4(a), the maximum kinetic energy is $U_{{\rm kin},{\rm max}}=86\,{\rm MeV}$
, shown in figure 4(a), the maximum kinetic energy is $U_{{\rm kin},{\rm max}}=86\,{\rm MeV}$![]() and, as expected, the energetic electron bunches are close to the symmetry axis. At the later time, $t\omega _{\rm pe}=550$
and, as expected, the energetic electron bunches are close to the symmetry axis. At the later time, $t\omega _{\rm pe}=550$![]() , shown in figure 4(b), the distribution peaks off-axis and the instantaneous maximum energy is $U_{{\rm kin},{\rm max}}=160\,{\rm MeV}$
, shown in figure 4(b), the distribution peaks off-axis and the instantaneous maximum energy is $U_{{\rm kin},{\rm max}}=160\,{\rm MeV}$![]() . The bunches are localized at the minimum of the electric field where the acceleration is the strongest, indicated by the red curves in the same figures. At the end of the simulation, the cumulative charge can be estimated to be $15\,{\rm pC}$
. The bunches are localized at the minimum of the electric field where the acceleration is the strongest, indicated by the red curves in the same figures. At the end of the simulation, the cumulative charge can be estimated to be $15\,{\rm pC}$![]() , assuming that the electron bunch is axisymmetric within a region of length $15\,\mathrm {\mu }{\rm m}$
, assuming that the electron bunch is axisymmetric within a region of length $15\,\mathrm {\mu }{\rm m}$![]() and a transverse extent $24\,\mathrm {\mu }{\rm m}$
and a transverse extent $24\,\mathrm {\mu }{\rm m}$![]() , given a laser wavelength of $800 \,{\rm nm}$
, given a laser wavelength of $800 \,{\rm nm}$![]() .
.

Figure 4. Spatial distribution of $n_{{\rm HE}}(\xi,y)$![]() at (a) $t\omega _{\rm pe}\approx 350$
at (a) $t\omega _{\rm pe}\approx 350$![]() and (b) $t\omega _{\rm pe}\approx 550$
and (b) $t\omega _{\rm pe}\approx 550$![]() . These times are marked with dashed lines in figure 3. The longitudinal electric field at the axis, ${E_L(\xi, y=0)/E_0}$
. These times are marked with dashed lines in figure 3. The longitudinal electric field at the axis, ${E_L(\xi, y=0)/E_0}$![]() , is indicated by the red curves (right axes).
, is indicated by the red curves (right axes).
We may quantify the angular spread of the electron beam by $\bar {\theta } =[\int \,{\rm d}^3\boldsymbol {p}(p_y/p_x)^2 f_e(\boldsymbol {p})$![]() / $\int \,{\rm d}^3\boldsymbol {p}f_e(\boldsymbol {p})]^{1/2}$
/ $\int \,{\rm d}^3\boldsymbol {p}f_e(\boldsymbol {p})]^{1/2}$![]() , with the integrals covering only the uppermost $10\,\%$
, with the integrals covering only the uppermost $10\,\%$![]() of the electron energies. We find that, in spite of the rich transverse dynamics, $\bar {\theta }$
of the electron energies. We find that, in spite of the rich transverse dynamics, $\bar {\theta }$![]() only reaches values of ${\sim }0.02$
only reaches values of ${\sim }0.02$![]() throughout the simulation. In the following section, we will delve into the reasons for the transverse dynamics, which shall also shed light on why the acceleration efficiency is reduced when moving from one to two dimensions.
throughout the simulation. In the following section, we will delve into the reasons for the transverse dynamics, which shall also shed light on why the acceleration efficiency is reduced when moving from one to two dimensions.
3 Phases of intensifying nonlinear effects
The regime explored in this work corresponds to the beat-wave autoresonance excitation of very large amplitude plasma waves and significant particle trapping, resulting in a number of 2-D nonlinear processes that affect the evolution of the plasma wave. It is interesting, however, that even in these extreme conditions, the nonlinearities do not destroy the laser–plasma coupling and the particle acceleration, but only partially degrade the process. Here, we review these effects, putting the focus on strong nonlinear effects appearing late in time, which impact the temporal coherence of the plasma wave. The understanding of these processes can provide guidance for future experiments, where they may be reduced or eliminated through appropriate schemes.
3.1 The weakly nonlinear stage
In the early phase of the evolution of the plasma wave – apart from a downward shift of its wavenumber as the plasma wave amplitude increases – the wavenumber spectrum is affected by forward Raman scattering at a slight angle with respect to the laser propagation. This leads to the appearance of a double signal in the electromagnetic spectrum, mainly around $k_L/k_{\rm pe} = 50$![]() (Forslund et al. Reference Forslund, Kindel, Mori, Joshi and Dawson1985), and a broadening of both the electromagnetic and the electron plasma wave spectrum in the transverse direction. Moreover, Stokes and anti-Stokes scattering results in harmonics of the electromagnetic wave. In Appendix B.1, we plot the Fourier spectrum of the waves, and all these components are clearly visible. At this stage, the only new effect compared with the 1-D case, discussed by Luo et al. (Reference Luo, Riconda, Pusztai, Grassi, Wurtele and Fülöp2024), is the transverse broadening and the double signal around $k_s/k_{\rm pe} = 50$
(Forslund et al. Reference Forslund, Kindel, Mori, Joshi and Dawson1985), and a broadening of both the electromagnetic and the electron plasma wave spectrum in the transverse direction. Moreover, Stokes and anti-Stokes scattering results in harmonics of the electromagnetic wave. In Appendix B.1, we plot the Fourier spectrum of the waves, and all these components are clearly visible. At this stage, the only new effect compared with the 1-D case, discussed by Luo et al. (Reference Luo, Riconda, Pusztai, Grassi, Wurtele and Fülöp2024), is the transverse broadening and the double signal around $k_s/k_{\rm pe} = 50$![]() , while the Stokes and anti-Stokes components and the longitudinal widening were already present in the 1-D simulations. Overall, the autoresonant excitation and the particle acceleration appear robust with respect to the presence of the transverse Raman scattering.
, while the Stokes and anti-Stokes components and the longitudinal widening were already present in the 1-D simulations. Overall, the autoresonant excitation and the particle acceleration appear robust with respect to the presence of the transverse Raman scattering.
Another 2-D effect that can be identified is due to the transverse variation of the laser intensity and the corresponding nonlinear correction to the wavelength. This leads to the formation of slightly curved plasma wave fronts, while the plasma wave structure remains coherent, as was also observed in some stimulated Raman scattering simulations (Rose & Yin Reference Rose and Yin2008; Yin et al. Reference Yin, Albright, Bowers, Daughton and Rose2008; Masson-Laborde et al. Reference Masson-Laborde, Rozmus, Peng, Pesme, Hüller, Casanova, Bychenkov, Chapman and Loiseau2010). More details on this wavefront bowing are given in Appendix B.2. Similarly to the mentioned parametric wave coupling processes, the wavefront bowing effect has no appreciable negative effect on the efficiency of the autoresonant PBWA.
3.2 Transverse magnetic field growth due to a Weibel-like instability
We now focus our attention on processes that become important around the time the acceleration efficiency starts to degrade compared with the 1-D simulations. The first of these effects is the growth of a Weibel-like instability (Fried Reference Fried1959; Weibel Reference Weibel1959), which provides a seed for subsequent plasma wave filamentation (Masson-Laborde et al. Reference Masson-Laborde, Rozmus, Peng, Pesme, Hüller, Casanova, Bychenkov, Chapman and Loiseau2010).
In figure 5, the longitudinally averaged transverse magnetic field $\bar {B}_z$![]() is shown as a function of the transverse coordinate $y$
is shown as a function of the transverse coordinate $y$![]() , normalized as $\bar {H}_z=e\bar {B}_z/m_e\omega _1$
, normalized as $\bar {H}_z=e\bar {B}_z/m_e\omega _1$![]() . The times shown illustrate the development of transverse magnetic field filaments (time increases from panel a to panel g). The average in the longitudinal direction is performed over the $\xi$
. The times shown illustrate the development of transverse magnetic field filaments (time increases from panel a to panel g). The average in the longitudinal direction is performed over the $\xi$![]() -range indicated by the dashed rectangle in figure 6(a). In this region, the plasma wave has a significant amplitude, but wave breaking has not yet been reached, and only a few particles are trapped. Indeed, the $\xi - p_x$
-range indicated by the dashed rectangle in figure 6(a). In this region, the plasma wave has a significant amplitude, but wave breaking has not yet been reached, and only a few particles are trapped. Indeed, the $\xi - p_x$![]() phase space (not shown here) has a very regular structure with longitudinal velocity up to $\simeq c$
phase space (not shown here) has a very regular structure with longitudinal velocity up to $\simeq c$![]() . Stronger particle acceleration is instead observed in the range $100< \xi < 150$
. Stronger particle acceleration is instead observed in the range $100< \xi < 150$![]() , leading to a more disordered magnetic field structure. In the early stages shown in figure 5(a,b), the magnetic field starts growing at the edges of the laser beams ($y\sim \pm 2.4{\rm \pi}$
, leading to a more disordered magnetic field structure. In the early stages shown in figure 5(a,b), the magnetic field starts growing at the edges of the laser beams ($y\sim \pm 2.4{\rm \pi}$![]() ) because of the large-scale current generated by the density and velocity perturbation in the plasma wave (with a homogeneous component plus one varying in the longitudinal direction with wavenumber $\sim 2 k_{\rm pe}$
) because of the large-scale current generated by the density and velocity perturbation in the plasma wave (with a homogeneous component plus one varying in the longitudinal direction with wavenumber $\sim 2 k_{\rm pe}$![]() ), as discussed by Gorbunov, Mora & Antonsen (Reference Gorbunov, Mora and Antonsen1996, Reference Gorbunov, Mora and Antonsen1997) and Sheng, Meyer-ter Vehn & Pukhov (Reference Sheng, Meyer-ter Vehn and Pukhov1998). The plasma current comes from the collective electron motion induced by the longitudinal electric field of the plasma wave. Note that in the central region of the laser beams, no magnetic field is generated, as the displacement current compensates for the plasma current. Some filaments start to appear in the central region and become more pronounced by the time shown in figure 5(c). As expected for a Weibel-like instability, the filaments grow with a typical wavenumber of the order of $k_{\rm pe}$
), as discussed by Gorbunov, Mora & Antonsen (Reference Gorbunov, Mora and Antonsen1996, Reference Gorbunov, Mora and Antonsen1997) and Sheng, Meyer-ter Vehn & Pukhov (Reference Sheng, Meyer-ter Vehn and Pukhov1998). The plasma current comes from the collective electron motion induced by the longitudinal electric field of the plasma wave. Note that in the central region of the laser beams, no magnetic field is generated, as the displacement current compensates for the plasma current. Some filaments start to appear in the central region and become more pronounced by the time shown in figure 5(c). As expected for a Weibel-like instability, the filaments grow with a typical wavenumber of the order of $k_{\rm pe}$![]() . Both wavelength and field amplitude increase with time (figure 5d–g) up to saturation, happening at $\omega _{\rm pe}t \simeq 430$
. Both wavelength and field amplitude increase with time (figure 5d–g) up to saturation, happening at $\omega _{\rm pe}t \simeq 430$![]() .
.

Figure 5. Longitudinally averaged transverse profiles of the $z$![]() -component of the magnetic field, taken at different times, normalized as $\bar {H}_z=e\bar {B}_z/m_e\omega _1$
-component of the magnetic field, taken at different times, normalized as $\bar {H}_z=e\bar {B}_z/m_e\omega _1$![]() . The averaging is performed over the same $\xi$
. The averaging is performed over the same $\xi$![]() -range as covered by the dashed rectangle in figure 6(a).
-range as covered by the dashed rectangle in figure 6(a).

Figure 6. (a) Spatial variation of the magnetic field $H_z=eB_z/(m_e\omega _1)$![]() at time $t \omega _{\rm pe}\approx 350$
at time $t \omega _{\rm pe}\approx 350$![]() . The filamentation of the magnetic field is clearly visible inside the magenta dashed box, where the plasma wave is driven to significant amplitudes while wave breaking is not reached. (b) Zoom-in of the magnetic field, taken from the region highlighted in panel (a). (c) Temperature anisotropy $A$
. The filamentation of the magnetic field is clearly visible inside the magenta dashed box, where the plasma wave is driven to significant amplitudes while wave breaking is not reached. (b) Zoom-in of the magnetic field, taken from the region highlighted in panel (a). (c) Temperature anisotropy $A$![]() in the same region as panel (b). Note that for the visibility, the range of $A$
in the same region as panel (b). Note that for the visibility, the range of $A$![]() is capped at $1$
is capped at $1$![]() , while $A$
, while $A$![]() can reach values of $\approx 3$
can reach values of $\approx 3$![]() but only in very restricted regions.
but only in very restricted regions.
To understand the origin of these magnetic field filaments, figure 6(a) shows the magnetic field $H_z=eB_z/(m_e\omega _1)$![]() as a function of $\xi$
as a function of $\xi$![]() and $y$
and $y$![]() at time $t\omega _{\rm pe}\approx 350$
at time $t\omega _{\rm pe}\approx 350$![]() (corresponding to the longitudinally averaged result of figure 5c). The transverse limits of the dashed magenta rectangle are located at $y=\pm {\rm \pi}$
(corresponding to the longitudinally averaged result of figure 5c). The transverse limits of the dashed magenta rectangle are located at $y=\pm {\rm \pi}$![]() ($y$
($y$![]() is normalized by the plasma wavenumber $k_{\rm pe}$
is normalized by the plasma wavenumber $k_{\rm pe}$![]() ) and are chosen such that the rectangle covers the flat-top region of the transverse profile of the laser beams. Inside this marked area, magnetic field filaments are clearly visible, as highlighted by figure 6(b) which shows a zoom-in on the same data.
) and are chosen such that the rectangle covers the flat-top region of the transverse profile of the laser beams. Inside this marked area, magnetic field filaments are clearly visible, as highlighted by figure 6(b) which shows a zoom-in on the same data.
To identify the drive of the instability and estimate its growth rate, we define the longitudinal and transverse thermal speeds $v_{tx}$![]() and $v_{ty}$
and $v_{ty}$![]() , respectively, as follows: $v_{tj}^2(\xi,y)=n^{-1}\int (v_{j}-V_j)^2 f(\xi,y,\boldsymbol {v})\,{\rm d}^3v$
, respectively, as follows: $v_{tj}^2(\xi,y)=n^{-1}\int (v_{j}-V_j)^2 f(\xi,y,\boldsymbol {v})\,{\rm d}^3v$![]() , where $n=\int f(\xi,y,\boldsymbol {v})\,{\rm d}^3v$
, where $n=\int f(\xi,y,\boldsymbol {v})\,{\rm d}^3v$![]() , $V_j=n^{-1}\int v_j f(\xi,y,\boldsymbol {v})\,{\rm d}^3v$
, $V_j=n^{-1}\int v_j f(\xi,y,\boldsymbol {v})\,{\rm d}^3v$![]() and $j=\{x,y\}$
and $j=\{x,y\}$![]() . These definitions allow us to introduce an effective temperature anisotropy parameter $A(\xi,y)=(v_{tx}^2/v_{ty}^2)-1$
. These definitions allow us to introduce an effective temperature anisotropy parameter $A(\xi,y)=(v_{tx}^2/v_{ty}^2)-1$![]() , adapting previous definitions (Ruyer et al. Reference Ruyer, Gremillet, Debayle and Bonnaud2015; Silva et al. Reference Silva, Schoeffler, Vieira, Hoshino, Fonseca and Silva2020; Silva, Afeyan & Silva Reference Silva, Afeyan and Silva2021) to our conditions. Its values are plotted in figure 6(c) at $t\omega _{\rm pe}\approx 350$
, adapting previous definitions (Ruyer et al. Reference Ruyer, Gremillet, Debayle and Bonnaud2015; Silva et al. Reference Silva, Schoeffler, Vieira, Hoshino, Fonseca and Silva2020; Silva, Afeyan & Silva Reference Silva, Afeyan and Silva2021) to our conditions. Its values are plotted in figure 6(c) at $t\omega _{\rm pe}\approx 350$![]() . Since most of the acceleration happens longitudinally, the longitudinal spread of the distribution function and hence the thermal speed is higher than the transverse one, yielding values $A>0$
. Since most of the acceleration happens longitudinally, the longitudinal spread of the distribution function and hence the thermal speed is higher than the transverse one, yielding values $A>0$![]() . Significant values of $A$
. Significant values of $A$![]() up to $\approx 3$
up to $\approx 3$![]() are reached in patches, as shown in figure 6(c). The anisotropy in the distribution makes the plasma unstable to a Weibel-like instability, leading to the growth of the magnetic filaments.Footnote 1
are reached in patches, as shown in figure 6(c). The anisotropy in the distribution makes the plasma unstable to a Weibel-like instability, leading to the growth of the magnetic filaments.Footnote 1
The time evolution of the maximum value of $|H_z|$![]() and the magnetic energy content inside the marked rectangular region of figure 6(a), $\mathcal {E}_{B_z}=\int \int {|eB_z/(m_e\omega _1)|^2}\,{\rm d}\xi \,{{\rm d} y}$
and the magnetic energy content inside the marked rectangular region of figure 6(a), $\mathcal {E}_{B_z}=\int \int {|eB_z/(m_e\omega _1)|^2}\,{\rm d}\xi \,{{\rm d} y}$![]() , are shown in figure 7, with solid and dash-dotted lines, respectively. We choose to focus only on the magnetic field inside the marked region, where the Weibel-like instability is the dominant effect that generates the magnetic filaments. We hence neglect the field growing at the intensity gradients of the laser beams and the more complex structures in the rear region ($100<\xi < 140$
, are shown in figure 7, with solid and dash-dotted lines, respectively. We choose to focus only on the magnetic field inside the marked region, where the Weibel-like instability is the dominant effect that generates the magnetic filaments. We hence neglect the field growing at the intensity gradients of the laser beams and the more complex structures in the rear region ($100<\xi < 140$![]() ), where efficient acceleration occurs near the axis, modifying the plasma wave structures and the phase space in a non-trivial way. This allows us to identify the typical growth of the field generated by the Weibel-like instability, as discussed below.
), where efficient acceleration occurs near the axis, modifying the plasma wave structures and the phase space in a non-trivial way. This allows us to identify the typical growth of the field generated by the Weibel-like instability, as discussed below.

Figure 7. Maximum of the $z$![]() -component of the magnetic field (solid black curve, $10 |H_z|_{\rm max}$
-component of the magnetic field (solid black curve, $10 |H_z|_{\rm max}$![]() ) and energy contained in the $z$
) and energy contained in the $z$![]() -component of the magnetic field (black dash-dotted, $\mathcal {E}_{B_z}$
-component of the magnetic field (black dash-dotted, $\mathcal {E}_{B_z}$![]() ); both within the region indicated by the dashed magenta rectangle in figure 6(a). The solid magenta line indicates an exponential growth with the estimated growth rate of the Weibel-like instability. The red dashed line is the quasi-longitudinal electric field energy $\mathcal {E}_{\rm in}$
); both within the region indicated by the dashed magenta rectangle in figure 6(a). The solid magenta line indicates an exponential growth with the estimated growth rate of the Weibel-like instability. The red dashed line is the quasi-longitudinal electric field energy $\mathcal {E}_{\rm in}$![]() and the blue dotted line is the electric field energy scattered outside the quasi-longitudinal wavenumber region $\mathcal {E}_{\rm out}$
and the blue dotted line is the electric field energy scattered outside the quasi-longitudinal wavenumber region $\mathcal {E}_{\rm out}$![]() .
.
The general trends of $\mathcal {E}_{B_z}$![]() and $|H_z|_{\rm max}$
and $|H_z|_{\rm max}$![]() are similar, and reflect the observations from figure 5. A first early rapid increase and saturation is observed at $t \omega _{\rm pe}\approx 190$
are similar, and reflect the observations from figure 5. A first early rapid increase and saturation is observed at $t \omega _{\rm pe}\approx 190$![]() . This initial phase of magnetic field generation is caused by the development of the self-generated quasi-static magnetic field as stated by Gorbunov et al. (Reference Gorbunov, Mora and Antonsen1996, Reference Gorbunov, Mora and Antonsen1997) and Sheng et al. (Reference Sheng, Meyer-ter Vehn and Pukhov1998). This is followed by another significant growth until $t\omega _{\rm pe}\approx 400$
. This initial phase of magnetic field generation is caused by the development of the self-generated quasi-static magnetic field as stated by Gorbunov et al. (Reference Gorbunov, Mora and Antonsen1996, Reference Gorbunov, Mora and Antonsen1997) and Sheng et al. (Reference Sheng, Meyer-ter Vehn and Pukhov1998). This is followed by another significant growth until $t\omega _{\rm pe}\approx 400$![]() , after which the magnetic field saturates around a higher level, with some oscillations. This second growth phase corresponds to the Weibel-like instability. The maximum growth rate of this Weibel-like instability, $\gamma _{\rm wb}$
, after which the magnetic field saturates around a higher level, with some oscillations. This second growth phase corresponds to the Weibel-like instability. The maximum growth rate of this Weibel-like instability, $\gamma _{\rm wb}$![]() , in terms of the anisotropy parameter above defined, is approximately given by (Okada, Yabe & Niu Reference Okada, Yabe and Niu1978; Satou & Okada Reference Satou and Okada1997; Sugie, Ogawa & Okada Reference Sugie, Ogawa and Okada2006; Okada & Ogawa Reference Okada and Ogawa2007; Zhou et al. Reference Zhou, Zheng, Liu and Cao2022)
, in terms of the anisotropy parameter above defined, is approximately given by (Okada, Yabe & Niu Reference Okada, Yabe and Niu1978; Satou & Okada Reference Satou and Okada1997; Sugie, Ogawa & Okada Reference Sugie, Ogawa and Okada2006; Okada & Ogawa Reference Okada and Ogawa2007; Zhou et al. Reference Zhou, Zheng, Liu and Cao2022)
Considering values extracted from the simulation for the transverse thermal speed $v_{ty}\approx 0.1c$![]() and temperature anisotropy $A \approx 2.5$
and temperature anisotropy $A \approx 2.5$![]() – where the latter is close to the upper end of the observed range of $A$
– where the latter is close to the upper end of the observed range of $A$![]() values – yields a growth rate $\gamma _{\rm wb}/\omega _{\rm pe}\approx 0.035$
values – yields a growth rate $\gamma _{\rm wb}/\omega _{\rm pe}\approx 0.035$![]() . Such an exponential growth, $\propto \exp (\gamma _{\rm wb}t)$
. Such an exponential growth, $\propto \exp (\gamma _{\rm wb}t)$![]() , is indicated by the magenta line in figure 7, showing a satisfactory agreement with the growth of $|H_z|_{\rm max}$
, is indicated by the magenta line in figure 7, showing a satisfactory agreement with the growth of $|H_z|_{\rm max}$![]() (solid black curve). We note that a similar comparison between the magnetic field growth and the predicted temperature anisotropy-driven Weibel growth rate at a lower laser intensity, $a=0.12$
(solid black curve). We note that a similar comparison between the magnetic field growth and the predicted temperature anisotropy-driven Weibel growth rate at a lower laser intensity, $a=0.12$![]() , showed similarly good agreement.
, showed similarly good agreement.
In the weakly nonlinear stage, discussed in detail in Appendix B.1, we already observed that forward/side Raman scattering and wave bending will tend to deform the plasma wave wavefront and introduce a transverse component to its wavenumber. The Weibel-like instability also affects the transverse wavenumber of the plasma wave, $k_{Ly}$![]() . To quantify the effect of the Weibel-like instability on the transverse wavenumber of the plasma wave $k_{Ly}$
. To quantify the effect of the Weibel-like instability on the transverse wavenumber of the plasma wave $k_{Ly}$![]() , we can take advantage of the fact that it will induce shorter transverse lengths (larger $k_{Ly}$
, we can take advantage of the fact that it will induce shorter transverse lengths (larger $k_{Ly}$![]() ) than that already identified in the weakly nonlinear stage. The longitudinal wavenumber $k_{Lx}$
) than that already identified in the weakly nonlinear stage. The longitudinal wavenumber $k_{Lx}$![]() instead is given by the matching condition, roughly $k_{Lx}\sim k_{\rm pe}$
instead is given by the matching condition, roughly $k_{Lx}\sim k_{\rm pe}$![]() , so we may consider a $k_{Lx}$
, so we may consider a $k_{Lx}$![]() range that provides a comfortable margin around this,Footnote 2 such as $k_{Lx}\in [0.5,1.5]k_{\rm pe}$
range that provides a comfortable margin around this,Footnote 2 such as $k_{Lx}\in [0.5,1.5]k_{\rm pe}$![]() .
.
The characteristic transverse broadening of the wavenumber spectrum due to the Raman process can be estimated as $\delta k_{Ly}=\sqrt {k_{\rm pe}^2-k_{\rm np}^2}$![]() , where $k_{\rm np}$
, where $k_{\rm np}$![]() is the nonlinear plasma wavenumber introduced in Appendix B.1 and discussed in figure 12 of Luo et al. (Reference Luo, Riconda, Pusztai, Grassi, Wurtele and Fülöp2024): $k_{\rm np}\approx k_{\rm pe} -3 k_{\rm pe} (E_L/E_0)^2/16$
is the nonlinear plasma wavenumber introduced in Appendix B.1 and discussed in figure 12 of Luo et al. (Reference Luo, Riconda, Pusztai, Grassi, Wurtele and Fülöp2024): $k_{\rm np}\approx k_{\rm pe} -3 k_{\rm pe} (E_L/E_0)^2/16$![]() . If $|k_{Ly}|<\delta k_{Ly}$
. If $|k_{Ly}|<\delta k_{Ly}$![]() , we expect Raman scattering and wavenumber nonlinearity to dominate, with a corresponding ‘quasi-longitudinal’ electric energy content $\mathcal {E}_{\rm in}$
, we expect Raman scattering and wavenumber nonlinearity to dominate, with a corresponding ‘quasi-longitudinal’ electric energy content $\mathcal {E}_{\rm in}$![]() . If $|k_{Ly}|>\delta k_{Ly}$
. If $|k_{Ly}|>\delta k_{Ly}$![]() , we expect additional processes, such as the Weibel-like instability to dominate, with electric energy content $\mathcal {E}_{\rm out}$
, we expect additional processes, such as the Weibel-like instability to dominate, with electric energy content $\mathcal {E}_{\rm out}$![]() . More specifically,
. More specifically,

Optimally, the energy is mostly contained in the quasi-longitudinal field, while non-ideal 2-D effects may scatter energy outside this region, and the ratio $\mathcal {E}_\textrm {out}/\mathcal {E}_\textrm {in}$![]() thus quantifies the importance of these 2-D effects that reduce the transverse coherence of the plasma wave. In figure 7, the electric energies $\mathcal {E}_{\textrm {in}}$
thus quantifies the importance of these 2-D effects that reduce the transverse coherence of the plasma wave. In figure 7, the electric energies $\mathcal {E}_{\textrm {in}}$![]() and $\mathcal {E}_{\textrm {out}}$
and $\mathcal {E}_{\textrm {out}}$![]() are also shown by red dashed and blue dotted lines, respectively. Most of the energy is contained in the quasi-longitudinal field that saturates around $t \omega _\textrm {pe}\approx 190$
are also shown by red dashed and blue dotted lines, respectively. Most of the energy is contained in the quasi-longitudinal field that saturates around $t \omega _\textrm {pe}\approx 190$![]() . The energy scattered outside this wavenumber region is approximately following the same trends as the $\mathcal {E}_{B_z}$
. The energy scattered outside this wavenumber region is approximately following the same trends as the $\mathcal {E}_{B_z}$![]() and $|H_z|_\textrm {max}$
and $|H_z|_\textrm {max}$![]() curves, with a first saturation around $t \omega _\textrm {pe}\approx 190$
curves, with a first saturation around $t \omega _\textrm {pe}\approx 190$![]() . A more pronounced growth phase occurs during $t\omega _\textrm {pe}\approx 300$
. A more pronounced growth phase occurs during $t\omega _\textrm {pe}\approx 300$![]() –$400$
–$400$![]() , when the magnetic fields grow due to the Weibel-like instability, followed by a second saturation. It is noteworthy that around the time of the onset of the Weibel-like instability, $\mathcal {E}_{\textrm {in}}$
, when the magnetic fields grow due to the Weibel-like instability, followed by a second saturation. It is noteworthy that around the time of the onset of the Weibel-like instability, $\mathcal {E}_{\textrm {in}}$![]() also starts to decrease, indicating a reduced coherence of the plasma wave, even if the ratio $\mathcal {E}_{\textrm {in}}/\mathcal {E}_{\textrm {out}}$
also starts to decrease, indicating a reduced coherence of the plasma wave, even if the ratio $\mathcal {E}_{\textrm {in}}/\mathcal {E}_{\textrm {out}}$![]() is always larger than one.
is always larger than one.
3.3 Strong nonlinearity and plasma wave filamentation
We have established the influence of Weibel-like instability on the transverse dynamics of the plasma waves: it gives rise to transverse magnetic perturbations and a scattering of electric field energy beyond that caused by Raman scattering, potentially leading to a reduction in the coherence of plasma waves. However, the direct impact of Weibel-like instability on the laser evolution in the plasma remains negligible as the instability quickly saturates. In this section, we explore how the later-stage evolution of the laser propagation in the strong-nonlinear phase, where density modulations and filamentation arise.
Figure 8 shows the wavenumber spectra of the electric field of the plasma wave $E_L$![]() (left column) and that of the electromagnetic wave $E_s$
(left column) and that of the electromagnetic wave $E_s$![]() (right column) at different time instances, with the corresponding wavenumbers denoted by $k_L$
(right column) at different time instances, with the corresponding wavenumbers denoted by $k_L$![]() and $k_s$
and $k_s$![]() , respectively. Here, we focus on times $t \omega _\textrm {pe} \ge 350$
, respectively. Here, we focus on times $t \omega _\textrm {pe} \ge 350$![]() . At early times ($t \omega _\textrm {pe}=350$
. At early times ($t \omega _\textrm {pe}=350$![]() ), the main mode spectrum of the plasma wave assumes an arc shape between the circle given by mode matching (dashed line) and that with the nonlinear shift accounted for (solid line). By the time $t \omega _\textrm {pe} = 630$
), the main mode spectrum of the plasma wave assumes an arc shape between the circle given by mode matching (dashed line) and that with the nonlinear shift accounted for (solid line). By the time $t \omega _\textrm {pe} = 630$![]() , the arc-shaped spectrum is not clearly seen any longer and a stronger transverse broadening is observed. In addition, in the vicinity of $k_{s,x}\approx 50$
, the arc-shaped spectrum is not clearly seen any longer and a stronger transverse broadening is observed. In addition, in the vicinity of $k_{s,x}\approx 50$![]() of the electromagnetic wave, the slightly downshifted and upshifted components start to evolve differently, the downshifted one spreading more in the transverse direction. The Stokes/anti-Stokes scattering is barely affected.
of the electromagnetic wave, the slightly downshifted and upshifted components start to evolve differently, the downshifted one spreading more in the transverse direction. The Stokes/anti-Stokes scattering is barely affected.

Figure 8. (a,b) Wavenumber spectra of the longitudinal electric field of the (a i,b i) plasma wave $E_L$![]() and the (a ii,b ii) electromagnetic wave $E_s$
and the (a ii,b ii) electromagnetic wave $E_s$![]() at different times. The green curves correspond to the solutions of (a i,b i) (B1) and (a ii,b ii) (B2). In panel (a i,b i), the solid (dashed) curves include (do not include) corrections for the nonlinear wavenumber shift. In panel (a ii,b ii), different green curves represent different scattering order. (c) Temporal evolution of the purely longitudinal ($k_{s,y}=0$
at different times. The green curves correspond to the solutions of (a i,b i) (B1) and (a ii,b ii) (B2). In panel (a i,b i), the solid (dashed) curves include (do not include) corrections for the nonlinear wavenumber shift. In panel (a ii,b ii), different green curves represent different scattering order. (c) Temporal evolution of the purely longitudinal ($k_{s,y}=0$![]() ) wavenumber component of the main modes of the two laser beams. Vertical red lines indicate the maximum bandwidth of the first laser beam $\Delta \omega /\omega _\textrm {pe}\approx 0.28$
) wavenumber component of the main modes of the two laser beams. Vertical red lines indicate the maximum bandwidth of the first laser beam $\Delta \omega /\omega _\textrm {pe}\approx 0.28$![]() .
.
In figure 8(c), the temporal evolution of the wavenumber spectrum $k_{s,x}$![]() of the two dominant laser beams is shown for the purely longitudinal mode ($k_{s,y}=0$
of the two dominant laser beams is shown for the purely longitudinal mode ($k_{s,y}=0$![]() ). The two vertical red lines indicate the maximum bandwidth of the first, chirped, laser beam – located at $k_{s,x}/k_\textrm {pe}=50$
). The two vertical red lines indicate the maximum bandwidth of the first, chirped, laser beam – located at $k_{s,x}/k_\textrm {pe}=50$![]() – that can be estimated as $\Delta \omega /\omega _\textrm {pe}\approx |\alpha |T_\textrm {pulse}=0.28$
– that can be estimated as $\Delta \omega /\omega _\textrm {pe}\approx |\alpha |T_\textrm {pulse}=0.28$![]() . Without the interaction of the lasers and the autoresonant creation of the plasma wave, the wavenumber spectrum of this chirped pulse would be nearly constant within this region. Instead, one observes that the signal in the vicinity of $k_{s,x}\approx 50$
. Without the interaction of the lasers and the autoresonant creation of the plasma wave, the wavenumber spectrum of this chirped pulse would be nearly constant within this region. Instead, one observes that the signal in the vicinity of $k_{s,x}\approx 50$![]() becomes very weak, leaving two bands on the sides, partly related to laser depletion due to the plasma wave excitation, also present in one dimension and observed in our previous simulations, and partly related to scattering from $k_{s,y}=0$
becomes very weak, leaving two bands on the sides, partly related to laser depletion due to the plasma wave excitation, also present in one dimension and observed in our previous simulations, and partly related to scattering from $k_{s,y}=0$![]() (plotted) to $k_{s,y}\ne 0$
(plotted) to $k_{s,y}\ne 0$![]() , as evident in figure 8(b ii).
, as evident in figure 8(b ii).
With the onset of autoresonance, considerable pump depletion, on account of the plasma wave excitation, is expected to take place. In terms of frequency, the width of the depleted gap can be estimated by $\Delta \omega _\textrm {eff}/\omega _\textrm {pe}\approx 3[1-(E_\textrm {RL}/E_0)^2]/16\approx 0.1$![]() . This is approximately a third of the overall bandwidth of the chirped beam, consistent with the observation. This also allows us to estimate the length over which autoresonance occurs, $L_\textrm {AR}\approx \Delta \omega _\textrm {eff}/\omega _\textrm {pe}/|\alpha |=75$
. This is approximately a third of the overall bandwidth of the chirped beam, consistent with the observation. This also allows us to estimate the length over which autoresonance occurs, $L_\textrm {AR}\approx \Delta \omega _\textrm {eff}/\omega _\textrm {pe}/|\alpha |=75$![]() . This distance $L_\textrm {AR}$
. This distance $L_\textrm {AR}$![]() is indeed representative of the spatial extent over which effective autoresonance takes place; see the $\xi \approx 125$
is indeed representative of the spatial extent over which effective autoresonance takes place; see the $\xi \approx 125$![]() –$200$
–$200$![]() range of figure 1(c).
range of figure 1(c).
Figure 9(a–c) captures snapshots of the plasma wave and the electromagnetic field, respectively, at time $t \omega _\textrm {pe}\approx 550$![]() , the time moment between those in figures 8(a) and 8(b). In figure 9(a), the electric field carried by the plasma wave $E_L$
, the time moment between those in figures 8(a) and 8(b). In figure 9(a), the electric field carried by the plasma wave $E_L$![]() over the range of $\xi \in [100,250]$
over the range of $\xi \in [100,250]$![]() is shown, where the transverse modulation is observed, particularly occurring over the range of $\xi \in [150,200]$
is shown, where the transverse modulation is observed, particularly occurring over the range of $\xi \in [150,200]$![]() , as exhibited in figure 9(b). The transverse regions where the beating patterns of the laser are weak, such as the gap at $|y|\approx 4$
, as exhibited in figure 9(b). The transverse regions where the beating patterns of the laser are weak, such as the gap at $|y|\approx 4$![]() in figure 9(c),Footnote 3 are correlated with a reduced plasma wave amplitude; see the reduced amplitude transverse bands in figure 9(b).
in figure 9(c),Footnote 3 are correlated with a reduced plasma wave amplitude; see the reduced amplitude transverse bands in figure 9(b).

Figure 9. At $t\omega _\textrm {pe}\approx 550$![]() , (a) the electric field of the plasma wave $E_L$
, (a) the electric field of the plasma wave $E_L$![]() , over the range $\xi \in [100,250]$
, over the range $\xi \in [100,250]$![]() , (b) $E_L$
, (b) $E_L$![]() in the range $\xi \in [150,200]$
in the range $\xi \in [150,200]$![]() and (c) the electric field of the electromagnetic wave $\tilde {a}$
and (c) the electric field of the electromagnetic wave $\tilde {a}$![]() , normalized by the initial total laser amplitude $a_1+a_2$
, normalized by the initial total laser amplitude $a_1+a_2$![]() in the range $\xi \in [150,200]$
in the range $\xi \in [150,200]$![]() .
.
At this stage of the evolution, we conjecture that the appearance of transverse structure of the plasma wave and of the laser pulses will self-sustain and enhance the transverse modulation. To justify this, we performed an almost identical simulation, adding a co-propagating probe laser with a linear polarization orthogonal to that of the dominant laser pulses, having only $5\,\%$![]() of their amplitudes; we denote the normalized electric field of this probe beam by $\tilde {a}_{p}$
of their amplitudes; we denote the normalized electric field of this probe beam by $\tilde {a}_{p}$![]() and its initial value by $a_{p}$
and its initial value by $a_{p}$![]() with $a_{p}=5\,\%a_{1,2}$
with $a_{p}=5\,\%a_{1,2}$![]() .
.
The density perturbation of the plasma wave ($\delta n_e+n_e)/n_e$![]() is shown in figure 10(a), along with the electric field of the probe laser in figure 10(b), at the same time instance as in figure 9. To emphasize the impact of the density perturbation on the laser field, in figure 10(b), we only plot the fields of the probe laser whenever $|\tilde {a}_{p}|/a_{p}\geq 1$
is shown in figure 10(a), along with the electric field of the probe laser in figure 10(b), at the same time instance as in figure 9. To emphasize the impact of the density perturbation on the laser field, in figure 10(b), we only plot the fields of the probe laser whenever $|\tilde {a}_{p}|/a_{p}\geq 1$![]() (these appear as blue and red spikes). The density perturbation modifies the index of refraction $\eta _r$
(these appear as blue and red spikes). The density perturbation modifies the index of refraction $\eta _r$![]() , thereby affecting the transverse propagation of the electromagnetic wave. We may approximate the index of refraction by
, thereby affecting the transverse propagation of the electromagnetic wave. We may approximate the index of refraction by
with the Lorentz factor $\gamma$![]() being comparable in magnitude to $\gamma _{\perp }=(1+a^2)^{1/2}$
being comparable in magnitude to $\gamma _{\perp }=(1+a^2)^{1/2}$![]() . To show the spatial variation of the refractive index, we draw the contours $\eta _r=0.9996$
. To show the spatial variation of the refractive index, we draw the contours $\eta _r=0.9996$![]() (white) and $n_r=0.9998$
(white) and $n_r=0.9998$![]() (black), calculated with the density variation shown in figure 10(a). As a result of the spatial variation of $\eta _r$
(black), calculated with the density variation shown in figure 10(a). As a result of the spatial variation of $\eta _r$![]() , the laser beams undergo fragmentation, with the various segments exhibiting different characteristics. Specifically, the intensity of the beamlets follow closely the density contours. Both the laser beams and the plasma have developed transverse modulation – a feature not present at earlier stages – marking the transition into the strongly nonlinear stage of the process. The evolution of the plasma wave in this stage have now a non-negligible impact on particle acceleration. The resulting reduced acceleration efficiency is apparent in figure 2(c), and a non-trivial transverse re-arrangement of the acceleration process is reflected in figures 3 and 4(b).
, the laser beams undergo fragmentation, with the various segments exhibiting different characteristics. Specifically, the intensity of the beamlets follow closely the density contours. Both the laser beams and the plasma have developed transverse modulation – a feature not present at earlier stages – marking the transition into the strongly nonlinear stage of the process. The evolution of the plasma wave in this stage have now a non-negligible impact on particle acceleration. The resulting reduced acceleration efficiency is apparent in figure 2(c), and a non-trivial transverse re-arrangement of the acceleration process is reflected in figures 3 and 4(b).

Figure 10. A low power ($a_{p}=5\,\%a_{1,2}$![]() ) probe laser with orthogonal polarization to the lasers that create the plasma wave co-propagates together with the two dominant laser beams. At the time $t\omega _\textrm {pe}=550$
) probe laser with orthogonal polarization to the lasers that create the plasma wave co-propagates together with the two dominant laser beams. At the time $t\omega _\textrm {pe}=550$![]() restricted to one plasma oscillation in $\xi$
restricted to one plasma oscillation in $\xi$![]() , (a) the plasma wave density profile and, in panel (b), blue (red) corresponds to large negative (positive) values of the probe laser field, and for the purpose of visibility, values of the probe field less in magnitude than the initial peak probe field are set to zero. The black and white contours correspond to refractive index values of $\eta _r=0.9998$
, (a) the plasma wave density profile and, in panel (b), blue (red) corresponds to large negative (positive) values of the probe laser field, and for the purpose of visibility, values of the probe field less in magnitude than the initial peak probe field are set to zero. The black and white contours correspond to refractive index values of $\eta _r=0.9998$![]() and $\eta _r=0.9996$
and $\eta _r=0.9996$![]() . See text for details.
. See text for details.
4 Discussion and conclusions
We have investigated autoresonant plasma beat-wave excitation in two dimensions with the PIC simulation Smilei. Primary laser and plasma parameters for the 2-D study correspond to those used in a 1-D simulation where large wave amplitudes and significant self-injection of electrons were observed. A number of 2-D features arise that were not previously seen using either simplified fluid models or 1-D kinetic simulations. For the case studied here, these effects occur after the peak electric field is reached and at wave amplitudes beyond the RL limit. That is, autoresonance works in two dimensions in that the peak field exceeded the RL limit, but at the same time, 2-D phenomena limit this field to a few oscillations beyond where it obtains its peak value.
As in one dimension, electrons are self-injected into the developing plasma wave structure and are accelerated, most efficiently along the axis of the laser beams. Various scattering processes – Raman side scattering or near-forward Raman scattering along with Stokes and anti-Stokes scattering – excite harmonics and circular patterns in wavenumber space, although these do not have much effect on the acceleration dynamics of self-injected electrons. This is related to the relatively low value of the density chosen in this paper, $n_e/n_{cr}=0.0004$![]() . As discussed explicitly by Luo et al. (Reference Luo, Riconda, Pusztai, Grassi, Wurtele and Fülöp2024), Stokes and anti-Stokes scattering, present both in one and two dimensions, do not significantly affect the laser beating at this density. Similarly, the near-forward Raman scattering observed in our 2-D PIC simulations does not have a significant impact on the plasma wave.
. As discussed explicitly by Luo et al. (Reference Luo, Riconda, Pusztai, Grassi, Wurtele and Fülöp2024), Stokes and anti-Stokes scattering, present both in one and two dimensions, do not significantly affect the laser beating at this density. Similarly, the near-forward Raman scattering observed in our 2-D PIC simulations does not have a significant impact on the plasma wave.
The phase fronts of the plasma wave develop curvature – a wavefront bowing (Rose & Yin Reference Rose and Yin2008; Yin et al. Reference Yin, Albright, Bowers, Daughton and Rose2008; Masson-Laborde et al. Reference Masson-Laborde, Rozmus, Peng, Pesme, Hüller, Casanova, Bychenkov, Chapman and Loiseau2010) – due to the transverse variation of laser intensity and corresponding variation in the plasma wave excitation. This is seen to change the transverse location of the peak field and the energy spectrum of electrons. Magnetic fields are self-generated by the large-scale currents driven by the density and velocity perturbation in the plasma wave (Gorbunov et al. Reference Gorbunov, Mora and Antonsen1996, Reference Gorbunov, Mora and Antonsen1997; Sheng et al. Reference Sheng, Meyer-ter Vehn and Pukhov1998). A Weibel-like instability (Weibel Reference Weibel1959) arising from velocity space anisotropy generates transverse magnetic field perturbations. The electric field, which is initially quasi-longitudinal, scatters in the transverse direction and the acceleration efficiency of the most energetic electrons starts to deviate from that seen in one dimension. Finally, we observe transverse filamentation and, as a consequence, the acceleration efficiency is further reduced; in this regime, the most energetic electrons are found off-axis.
Novel schemes to avoid diffractive and dephasing limits such as those based on Bessel beams (Caizergues et al. Reference Caizergues, Smartsev, Malka and Thaury2020; Ponomareva & Shevchenko Reference Ponomareva and Shevchenko2023) place requirements on chirped pulses; their compatibility with autoresonant excitation is a topic for future study. Transverse effects originating from the defocusing of the laser beams may reduce acceleration efficiency, which motivates further studies using a plasma channel to guide the laser beams. In conclusion, this initial study of kinetic effects in autoresonant plasma beat-wave excitation indicates that 2-D effects can become important and thus the design of any accelerator scheme based on this will require 2-D analysis and optimization. The computational expense of 2-D studies supports the development of reduced models of the 2-D problem, even if some of the phenomena described in this paper, such as the Weibel-like instability – related to a complex evolution of the electron phase space – might be challenging to model and require further kinetic studies.
Acknowledgements
The authors are grateful to S. Hüller and D. Maslarova for fruitful discussions.
Editor L.O. Silva thanks the referees for their advice in evaluating this article.
Funding
This work was supported by the Knut and Alice Wallenberg Foundation (Grant No. KAW 2020.0111). The computations were enabled by resources provided by the National Academic Infrastructure for Supercomputing in Sweden (NAISS), partially funded by the Swedish Research Council through grant agreement No. 2022-06725 and 2021-03943. C.R. and J.S.W. thank the Berkeley-France Fund for support of this research.
Declaration of interests
The authors report no conflict of interest.
Author contributions
M.L. performed the simulations. All authors contributed equally to analysing data and reaching conclusions, and in writing the paper.
Appendix A. Precise control of the 1-D autoresonant PBWA
In our previous paper (Luo et al. Reference Luo, Riconda, Pusztai, Grassi, Wurtele and Fülöp2024), we have identified laser and plasma parameters that lead to an effective acceleration of self-injected electrons. These parameters are summarized in table 2 and the acceleration is not sensitive to small variations around these values. A sensitive parameter is the laser duration for which we found a constraint, as indicated in the last column, $T_\textrm {pulse}\lesssim 100{\rm \pi} /\omega _\textrm {pe}$![]() . To clearly identify the regime of autoresonant PBWA of interest for us, we conducted 1-D kinetic simulations where we varied the laser duration as a key control parameter. The other parameters were chosen as follows: normalized laser electric field $a_1=a_2 = 0.2$
. To clearly identify the regime of autoresonant PBWA of interest for us, we conducted 1-D kinetic simulations where we varied the laser duration as a key control parameter. The other parameters were chosen as follows: normalized laser electric field $a_1=a_2 = 0.2$![]() , a homogeneous plasma density of $n_e/n_{cr} = 0.0004$
, a homogeneous plasma density of $n_e/n_{cr} = 0.0004$![]() , following a short linear density ramp, a chirp of rate $\alpha =-0.0014$
, following a short linear density ramp, a chirp of rate $\alpha =-0.0014$![]() is applied to the first laser beam ($a_1$
is applied to the first laser beam ($a_1$![]() ) and the frequency difference between the two lasers $\Delta \omega$
) and the frequency difference between the two lasers $\Delta \omega$![]() meets the resonant frequency $\omega _\textrm {pe}$
meets the resonant frequency $\omega _\textrm {pe}$![]() at $t_0=22.5{\rm \pi}$
at $t_0=22.5{\rm \pi}$![]() .
.
Table 2. The optimal laser and plasma parameters in the homogeneous plasma to drive autoresonant PBWA.

In figure 11(a), the amplitude of the plasma wave normalized by the RL limit, $E_L/E_\textrm {RL}$![]() , is shown as a function of laser duration $T_\textrm {pulse}\omega _\textrm {pe}$
, is shown as a function of laser duration $T_\textrm {pulse}\omega _\textrm {pe}$![]() , comparing 1-D kinetic simulation results (red up-triangles) and a fluid model (red curve). The two horizontal dashed black lines represent the RL limit $E_\textrm {RL}$
, comparing 1-D kinetic simulation results (red up-triangles) and a fluid model (red curve). The two horizontal dashed black lines represent the RL limit $E_\textrm {RL}$![]() and the wave-breaking limit $E_0$
and the wave-breaking limit $E_0$![]() , respectively. An increase in the laser duration leads to higher amplitude plasma waves. Below the wave-breaking limit, the kinetic simulation results follow the predictions of the fluid model with reasonable agreement. However, while the electric field in the kinetic simulations represents a real upper bound for the kinetic results, which is where they saturate for $T_\textrm {pulse}\omega _\textrm {pe}\gtrsim 200$
, respectively. An increase in the laser duration leads to higher amplitude plasma waves. Below the wave-breaking limit, the kinetic simulation results follow the predictions of the fluid model with reasonable agreement. However, while the electric field in the kinetic simulations represents a real upper bound for the kinetic results, which is where they saturate for $T_\textrm {pulse}\omega _\textrm {pe}\gtrsim 200$![]() , the fluid predictions keep increasing with $T_\textrm {pulse}$
, the fluid predictions keep increasing with $T_\textrm {pulse}$![]() .
.

Figure 11. Comparisons of 1-D PIC and 1-D fluid models for the autoresonant excitation with parameters in table 2. (a) $E_L/E_\textrm {RL}$![]() . The red up-triangles represent the kinetic results, while the red line plots the results of the fluid model, as a function of laser duration $T_\textrm {pulse}\omega _\textrm {pe}$
. The red up-triangles represent the kinetic results, while the red line plots the results of the fluid model, as a function of laser duration $T_\textrm {pulse}\omega _\textrm {pe}$![]() ; (b) the maximum energy gradient in units of the normalized distance $xk_\textrm {pe}$
; (b) the maximum energy gradient in units of the normalized distance $xk_\textrm {pe}$![]() , $\textrm {MeV}/(xk_\textrm {pe})$
, $\textrm {MeV}/(xk_\textrm {pe})$![]() , over the acceleration length $Lk_\textrm {pe}\approx 500$
, over the acceleration length $Lk_\textrm {pe}\approx 500$![]() . The blue down triangles represent the kinetic results and the blue line is an estimation based on the fluid model.
. The blue down triangles represent the kinetic results and the blue line is an estimation based on the fluid model.
In figure 11(b), we show the energy gradient (in units of $\textrm {MeV}/(xk_\textrm {pe})$![]() ) experienced by the most energetic accelerated particles over the acceleration length of $Lk_\textrm {pe}\approx 500$
) experienced by the most energetic accelerated particles over the acceleration length of $Lk_\textrm {pe}\approx 500$![]() , again, with a comparison of kinetic simulation results (blue down-triangles) and a fluid estimate (blue curve). The latter is calculated as $E_L m_e c^2/E_0$
, again, with a comparison of kinetic simulation results (blue down-triangles) and a fluid estimate (blue curve). The latter is calculated as $E_L m_e c^2/E_0$![]() , where $E_L$
, where $E_L$![]() can be obtained from the fluid model. The kinetic simulation results cannot exceed the wave-breaking estimate, i.e. $\lesssim 0.5$
can be obtained from the fluid model. The kinetic simulation results cannot exceed the wave-breaking estimate, i.e. $\lesssim 0.5$![]() . Hence, by varying the laser duration for fixed optimal laser parameters, the plasma wave amplitude and the energy gradient experienced by the accelerated particles can be well controlled. Thus, a control of the electron energization is possible, at least until the onset of multiple-dimensional effects.
. Hence, by varying the laser duration for fixed optimal laser parameters, the plasma wave amplitude and the energy gradient experienced by the accelerated particles can be well controlled. Thus, a control of the electron energization is possible, at least until the onset of multiple-dimensional effects.
Appendix B. Processes in the linear and weak nonlinear phases
B.1 Side-scattering or near-forward Raman scattering
In figure 12(a i,b i,c i), we observe that a distinct signal of the plasma wave emerges during the initial linear stage, characterized by wavenumbers $k_{L,x}\approx k_\textrm {pe}$![]() and $k_{L,y}\approx 0$
and $k_{L,y}\approx 0$![]() , as depicted in figure 12(a i). Later, when autoresonance becomes significant, figure 12(b i), the amplitude of the plasma wave intensifies, accompanied by a reduction in wavenumber, approximately $k_{L,x}< k_\textrm {pe}$
, as depicted in figure 12(a i). Later, when autoresonance becomes significant, figure 12(b i), the amplitude of the plasma wave intensifies, accompanied by a reduction in wavenumber, approximately $k_{L,x}< k_\textrm {pe}$![]() . Additionally, non-zero components of $k_{L,y}$
. Additionally, non-zero components of $k_{L,y}$![]() become apparent, along with a weak harmonic signal, roughly $k_{L,x}\approx 2k_\textrm {pe}$
become apparent, along with a weak harmonic signal, roughly $k_{L,x}\approx 2k_\textrm {pe}$![]() . The arc-shaped signal of the dominant wavenumber is a result of side-scattering or near-forward Raman scattering of the laser beams.
. The arc-shaped signal of the dominant wavenumber is a result of side-scattering or near-forward Raman scattering of the laser beams.

Figure 12. Fourier spectra of the wavenumber carried by the longitudinal electric field $E_L$![]() (a i,b i,c i) and the electromagnetic wave $E_s$
(a i,b i,c i) and the electromagnetic wave $E_s$![]() (a ii,b ii,c ii) are depicted at various moments, satisfying the temporal constraint $t\omega _\textrm {pe}\leq 350$
(a ii,b ii,c ii) are depicted at various moments, satisfying the temporal constraint $t\omega _\textrm {pe}\leq 350$![]() . The green lines correspond to the solutions of (a i,b i,c i) (B1) and(a ii,b ii,c ii) (B2). In panels (a i,b i,c i), the solid line takes into account the nonlinear wavelength shift due to the relativistic effect, while the dotted line neglects this effect.
. The green lines correspond to the solutions of (a i,b i,c i) (B1) and(a ii,b ii,c ii) (B2). In panels (a i,b i,c i), the solid line takes into account the nonlinear wavelength shift due to the relativistic effect, while the dotted line neglects this effect.
The plasma wavenumber matching condition during Raman scattering is given by
Here, $\delta k_L$![]() represents the nonlinear wavenumber shift. Drawing on insights from Sprangle, Esarey & Ting (Reference Sprangle, Esarey and Ting1990a,Reference Sprangle, Esarey and Tingb) and Esarey et al. (Reference Esarey, Schroeder and Leemans2009), we can approximate the nonlinear plasma wavelength as $\lambda _{nL}=\lambda _p(1+3(E_L/E_0)^2/16)$
represents the nonlinear wavenumber shift. Drawing on insights from Sprangle, Esarey & Ting (Reference Sprangle, Esarey and Ting1990a,Reference Sprangle, Esarey and Tingb) and Esarey et al. (Reference Esarey, Schroeder and Leemans2009), we can approximate the nonlinear plasma wavelength as $\lambda _{nL}=\lambda _p(1+3(E_L/E_0)^2/16)$![]() , where $\lambda _p$
, where $\lambda _p$![]() is the linear plasma wavelength. As a result, the nonlinear plasma wavenumber can be computed as $k_{Lp}=2{\rm \pi} /\lambda _{Lp}\approx k_\textrm {pe}+\delta k_L$
is the linear plasma wavelength. As a result, the nonlinear plasma wavenumber can be computed as $k_{Lp}=2{\rm \pi} /\lambda _{Lp}\approx k_\textrm {pe}+\delta k_L$![]() , with $\delta k_L/k_\textrm {pe}=-3(E_L/E_0)^2/16$
, with $\delta k_L/k_\textrm {pe}=-3(E_L/E_0)^2/16$![]() . The matching condition, (B1), is indicated in figure 12 without nonlinear wavenumber shift (dashed green curve), and with the above estimate of the wavenumber shift (solid curve), where, to provide an upper bound, $E_L$
. The matching condition, (B1), is indicated in figure 12 without nonlinear wavenumber shift (dashed green curve), and with the above estimate of the wavenumber shift (solid curve), where, to provide an upper bound, $E_L$![]() was set to be the highest electric field observed in the simulation $E_{L,{\rm max}}$
was set to be the highest electric field observed in the simulation $E_{L,{\rm max}}$![]() to estimate $\delta k_L$
to estimate $\delta k_L$![]() . These two curves provide a reasonably accurate bound of the spectral features seen in the simulation.
. These two curves provide a reasonably accurate bound of the spectral features seen in the simulation.
The wavenumber spectrum of the electromagnetic wave is presented in figure 12(a ii,b ii,c ii) for the same time instances. Initially, in figure 12(a ii), the signal of the two dominant laser beams is evident. As time progresses, in addition to these two components, other harmonics resulting from Stokes or anti-Stokes scattering become visible, as shown in figures 12(b ii) and 12(c ii). Analogously to (B1), these arc-shaped signals of different components can be described by a matching condition of these scattering processes
Here, $n$![]() denotes the scattering order, and (B2) is plotted in figure 12(a ii,b ii,c ii) using green lines. The solutions of (B2) with $n=-2$
denotes the scattering order, and (B2) is plotted in figure 12(a ii,b ii,c ii) using green lines. The solutions of (B2) with $n=-2$![]() , $-1$
, $-1$![]() , $0$
, $0$![]() and $1$
and $1$![]() are represented by the solid, dashed, dotted and dash-dotted lines, respectively, closely agreeing with the spectrum seen in the simulation. It is worth noting that the spectral feature of the first laser beam, i.e. $k_{s,x}\approx 50 k_\textrm {pe}$
are represented by the solid, dashed, dotted and dash-dotted lines, respectively, closely agreeing with the spectrum seen in the simulation. It is worth noting that the spectral feature of the first laser beam, i.e. $k_{s,x}\approx 50 k_\textrm {pe}$![]() , gradually splits into two pieces, from figure 12(a ii) to figure 12(c ii). Over the time range shown here, these two parts in the vicinity of $k_{s,x}\approx 50$
, gradually splits into two pieces, from figure 12(a ii) to figure 12(c ii). Over the time range shown here, these two parts in the vicinity of $k_{s,x}\approx 50$![]() remain nearly symmetrical. This peculiar feature, which later becomes asymmetric is further discussed in § 3.3.
remain nearly symmetrical. This peculiar feature, which later becomes asymmetric is further discussed in § 3.3.
As discussed by Rose & Yin (Reference Rose and Yin2008) and Yin et al. (Reference Yin, Albright, Bowers, Daughton and Rose2008), the trapped particle modulational instability (TPMI) emerges as an alternative mechanism to cause plasma wave filamentation. This instability, whenever important, induces another wavenumber shift in addition to that caused by the relativistic nonlinearity, and its growth rate is proportional to this shift (Dewar, Kruer & Manheimer Reference Dewar, Kruer and Manheimer1972; Rose Reference Rose2004). In the cases considered here, however, the wavenumber spectrum can be well described with the nonlinear shift alone (see the discussion concerning figure 12), indicating that TPMI plays a negligible role.
B.2 Wavefront bowing of the plasma wave
Wavefront bowing emerges as a 2-D effect related to the transverse variation of nonlinear wavenumber shift. In figures 13(a) and 13(b), the longitudinal electric field $E_L$![]() corresponding to the plasma wave, and the electric field $\tilde {a}_s$
corresponding to the plasma wave, and the electric field $\tilde {a}_s$![]() of the laser beams are presented, respectively, at the time moment of $t\omega _\textrm {pe}\approx 350$
of the laser beams are presented, respectively, at the time moment of $t\omega _\textrm {pe}\approx 350$![]() , corresponding to the time of figures 12(c i) and 12(c ii). In figure 13(a), significant wavefront bowing is observed within the range of $\xi \in [150,180]$
, corresponding to the time of figures 12(c i) and 12(c ii). In figure 13(a), significant wavefront bowing is observed within the range of $\xi \in [150,180]$![]() . The primary reason for this is the transverse dependence of the laser amplitude. The higher plasma wave amplitude on the middle of the laser beams corresponds to a longer wavelength; thus the wave front in this region lags behind that at the edges of the laser beam. Notably, the beating pattern of the two laser beams, shown in figure 13(b), remains regular, indicating that the influence of the density perturbation on the laser propagation remains negligible at these early times.
. The primary reason for this is the transverse dependence of the laser amplitude. The higher plasma wave amplitude on the middle of the laser beams corresponds to a longer wavelength; thus the wave front in this region lags behind that at the edges of the laser beam. Notably, the beating pattern of the two laser beams, shown in figure 13(b), remains regular, indicating that the influence of the density perturbation on the laser propagation remains negligible at these early times.

Figure 13. (a) Plasma electric field $E_L$![]() normalized by the RL limit and (b) electromagnetic wave $\tilde {a}$
normalized by the RL limit and (b) electromagnetic wave $\tilde {a}$![]() normalized by the initial laser amplitude $a_1+a_2$
normalized by the initial laser amplitude $a_1+a_2$![]() at the time moment $t\omega _\textrm {pe}\approx 350$
at the time moment $t\omega _\textrm {pe}\approx 350$![]() .
.
In conclusion, during the linear and weak-nonlinear phases, $t\omega _\textrm {pe}\le 350$![]() , the structure of the autoresonant plasma wave remains stable and regular, as supported by figure 1, despite the observed wavefront bowing in figure 13. Consequently, the acceleration process of energetic electrons in two dimensions remains similar to that in the 1-D case, as depicted in figure 2(c). At this time, the majority of these particles are concentrated centrally in the transverse direction, as evident in figures 3 and 4(a).
, the structure of the autoresonant plasma wave remains stable and regular, as supported by figure 1, despite the observed wavefront bowing in figure 13. Consequently, the acceleration process of energetic electrons in two dimensions remains similar to that in the 1-D case, as depicted in figure 2(c). At this time, the majority of these particles are concentrated centrally in the transverse direction, as evident in figures 3 and 4(a).