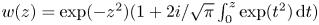1 Introduction
The investigation of the linear-stability properties of magnetically confined plasmas is crucial for the design of magnetic-confinement-fusion devices. The heat and particle losses in these devices are dominated by turbulent fluctuations, which are themselves excited by linear instabilities driven by the gradients of the plasma equilibrium (Rudakov & Sagdeev Reference Rudakov and Sagdeev1961; Coppi, Rosenbluth & Sagdeev Reference Coppi, Rosenbluth and Sagdeev1967; Pogutse Reference Pogutse1968; Guzdar et al. Reference Guzdar, Chen, Tang and Rutherford1983; Hugill Reference Hugill1983; Liewer Reference Liewer1985; Waltz Reference Waltz1988; Wootton et al. Reference Wootton, Carreras, Matsumoto, McGuire, Peebles, Ritz, Terry and Zweben1990; Cowley, Kulsrud & Sudan Reference Cowley, Kulsrud and Sudan1991; Kotschenreuther et al. Reference Kotschenreuther, Dorland, Beer and Hammett1995; Xanthopoulos et al. Reference Xanthopoulos, Merz, Görler and Jenko2007; Ongena et al. Reference Ongena, Koch, Wolf and Zohm2016). In most cases, the strong toroidal magnetic field constrains the plasma fluctuations to have typical temporal scales that are slow compared to the frequency of the Larmor motion of the particles, and to be anisotropic in space: length scales along the magnetic field are comparable to the size of the device, while those perpendicular to it are comparable to the Larmor radii of the particles. Therefore, the plasma dynamics can often be treated using the gyrokinetic formalism (Frieman & Chen Reference Frieman and Chen1982; Sugama et al. Reference Sugama, Okamoto, Horton and Wakatani1996; Howes et al. Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006; Abel et al. Reference Abel, Plunk, Wang, Barnes, Cowley, Dorland and Schekochihin2013; Catto Reference Catto2019).
When solving the linear gyrokinetic equation, one inevitably encounters resonant velocity-space integrals that need to be evaluated, analytically or numerically, to obtain the dispersion relation for the linear modes present within the system. The most basic of these resonances results from the parallel (to the magnetic field) streaming of particles, first discussed by Landau (Reference Landau1946). However, in the presence of an inhomogeneous equilibrium magnetic field, one is presented with a qualitatively different type of resonance due to the magnetic drifts of the particles. Evaluating these resonant integrals analytically, in the presence of both parallel streaming and magnetic drifts that are constant along the magnetic field, and without further approximations (such as those used in, e.g. Terry, Anderson & Horton Reference Terry, Anderson and Horton1982; Kim et al. Reference Kim, Kishimoto, Horton and Tajima1994) has remained an open research question, despite some progress being made numerically (Gürcan Reference Gürcan2014; Gültekin & Gürcan Reference Gültekin and Gürcan2018; Gültekin & Gürcan Reference Gültekin and Gürcan2020; Parisi et al. Reference Parisi, Parra, Roach, Giroud, Dorland, Hatch, Barnes, Hillesheim, Aiba and Ball2020). However, it is well known that there are instabilities that exist only in the presence of curved magnetic fields, e.g. the toroidal ion-temperature-gradient (ITG) instability (Pogutse Reference Pogutse1968; Guzdar et al. Reference Guzdar, Chen, Tang and Rutherford1983; Waltz Reference Waltz1988; Kotschenreuther et al. Reference Kotschenreuther, Dorland, Beer and Hammett1995). Often, such instabilities are the dominant ones in toroidal plasmas. Thus, the exact inclusion of the magnetic-drift resonance in the analytical theory of linear gyrokinetics is expected to lead to qualitative changes in the behaviour of the resulting dispersion relation and to allow for a more complete treatment of the linear-stability properties of strongly magnetised plasmas.
In this work, we present closed forms for the aforementioned resonant integrals. These are written in terms of the plasma dispersion function (Faddeeva & Terent'ev Reference Faddeeva and Terent'ev1954; Fried & Conte Reference Fried and Conte1961). They allow us to find a closed expression for the drift-kinetic dispersion relation, or an absolutely convergent series for the gyrokinetic one via Taylor expansions. The inclusion of magnetic drifts in the linear gyrokinetic problem introduces two distinct changes: (i) quantitatively, in that it significantly modifies the growth rates and frequencies of linear solutions; and (ii) qualitatively, by introducing a multivalued dispersion function. The latter has important consequences for the form of the dispersion relation and its solution, some of which have already been described in the literature (Kuroda et al. Reference Kuroda, Sugama, Kanno, Okamoto and Horton1998; Sugama Reference Sugama1999).
The rest of the paper is organised as follows. We begin by summarising how the gyrokinetic dispersion relation, and the resonant velocity-space integrals of which it is comprised, emerge from the Fourier–Laplace transform of the linear gyrokinetic equations in § 2. Then, in § 3, we discuss already-known solutions for these integrals and the asymptotic limits in which they apply. The main result of this work is presented in § 4, where we derive the exact solution to one particular resonant integral – the ‘generalised plasma dispersion function’ – to which all others will be related. In § 5.1, we show both analytically and numerically that the generalised plasma dispersion function asymptotes to the known solutions in the cases of zero magnetic curvature and of two-dimensional (2-D) perturbations, while § 5.2 demonstrates that our expressions are in agreement with the numerical solver published by Gürcan (Reference Gürcan2014). Section 6 discusses the analytic continuation of these functions and the subsequent solution to the inverse-Laplace-transform problem by which we obtain the solution to the linear gyrokinetic system. In § 7, we show how the results obtained in § 4 can be generalised to the gyrokinetic case via absolutely convergent Taylor expansions. In § 8, we give an example calculation for the electrostatic ITG instability and compare it with known kinetic and fluid limits. Finally, our results are summarised and possible extensions discussed in § 9.
2 Collisionless gyrokinetic linear theory
In this section, we demonstrate how the resonant kinetic integrals that are the main focus of this paper emerge naturally from considerations of linear, collisionless local gyrokinetic theory with constant geometric coefficients [see the discussion following (2.10)]. Readers already familiar with gyrokinetic theory may wish to skip ahead to § 2.3, working backwards where further clarification is required.
2.1 Gyrokinetics
As is often the case in the study of magnetically confined plasmas, we shall assume that the fluctuations within our plasma obey the standard gyrokinetic ordering (see, e.g. Abel et al. Reference Abel, Plunk, Wang, Barnes, Cowley, Dorland and Schekochihin2013 or Catto Reference Catto2019); that is, for fluctuations with a characteristic frequency $\omega$![]() and wavenumbers $k_\parallel$
and wavenumbers $k_\parallel$![]() and $k_\perp$
and $k_\perp$![]() parallel and perpendicular to the equilibrium magnetic field direction $\boldsymbol {b}_0 = \boldsymbol {B}_0/B_0$
parallel and perpendicular to the equilibrium magnetic field direction $\boldsymbol {b}_0 = \boldsymbol {B}_0/B_0$![]() , we have
, we have
where $\varOmega _s = q_s B_0/m_s c$![]() is the cyclotron frequency of species $s$
is the cyclotron frequency of species $s$![]() with charge $q_s$
with charge $q_s$![]() , equilibrium density and temperature $n_{0s}$
, equilibrium density and temperature $n_{0s}$![]() and $T_{0s}$
and $T_{0s}$![]() , respectively, mass $m_s$
, respectively, mass $m_s$![]() and thermal speed $v_{{\rm th}s} = \sqrt {2T_{0s}/m_s}$
and thermal speed $v_{{\rm th}s} = \sqrt {2T_{0s}/m_s}$![]() , $\nu _{s s'}$
, $\nu _{s s'}$![]() is the typical collision frequency, $\rho _s = v_{{\rm th}s}/|\varOmega _s|$
is the typical collision frequency, $\rho _s = v_{{\rm th}s}/|\varOmega _s|$![]() is the thermal Larmor radius, $\delta \! B_\parallel$
is the thermal Larmor radius, $\delta \! B_\parallel$![]() and $\delta \! \boldsymbol {B}_\perp$
and $\delta \! \boldsymbol {B}_\perp$![]() are the fluctuations of the magnetic field parallel and perpendicular to the equilibrium direction, respectively, and $L$
are the fluctuations of the magnetic field parallel and perpendicular to the equilibrium direction, respectively, and $L$![]() is a typical equilibrium length scale. It is assumed that all equilibrium quantities evolve on the (long) transport timescale $\tau _E^{-1} \sim (\rho _s/L)^3 \varOmega _s$
is a typical equilibrium length scale. It is assumed that all equilibrium quantities evolve on the (long) transport timescale $\tau _E^{-1} \sim (\rho _s/L)^3 \varOmega _s$![]() , and so will be considered static throughout the remainder of this paper.
, and so will be considered static throughout the remainder of this paper.
Under the ordering of (2.1), the perturbed distribution function $\delta \! f_s$![]() consists of the Boltzmann and gyrokinetic parts:
consists of the Boltzmann and gyrokinetic parts:
where $\boldsymbol {R}_s = \boldsymbol {r} - \boldsymbol {b}_0 \times \boldsymbol {v}_\perp /\varOmega _s$![]() is the guiding-centre position, and $h_s$
is the guiding-centre position, and $h_s$![]() evolves according to the gyrokinetic equation
evolves according to the gyrokinetic equation
In the above, and throughout this paper, $\left \langle \cdots \right \rangle _{\boldsymbol {R}_s}$![]() denotes the standard gyroaverage at constant $\boldsymbol {R}_s$
denotes the standard gyroaverage at constant $\boldsymbol {R}_s$![]() . Here, $\chi = \phi - \boldsymbol {v}\boldsymbol {\cdot } \boldsymbol {A}/c$
. Here, $\chi = \phi - \boldsymbol {v}\boldsymbol {\cdot } \boldsymbol {A}/c$![]() is the gyrokinetic potential ($\phi$
is the gyrokinetic potential ($\phi$![]() and $\boldsymbol {A}$
and $\boldsymbol {A}$![]() are the scalar and vector potential, respectively, under the Coulomb gauge ${\boldsymbol {\nabla }} \boldsymbol {\cdot } \boldsymbol {A} = 0$
are the scalar and vector potential, respectively, under the Coulomb gauge ${\boldsymbol {\nabla }} \boldsymbol {\cdot } \boldsymbol {A} = 0$![]() ) that gives rise to the drift velocity
) that gives rise to the drift velocity
which includes the $\boldsymbol {E} \times \boldsymbol {B}$![]() drift, the parallel streaming along perturbed field lines and the ${\boldsymbol {\nabla }} \! B$
drift, the parallel streaming along perturbed field lines and the ${\boldsymbol {\nabla }} \! B$![]() drift associated with the perturbed magnetic field. This gives rise to nonlinearities (with which we will not be concerned in this paper), as well as the familiar gyrokinetic drive associated with the equilibrium distribution $f_{0s}$
drift associated with the perturbed magnetic field. This gives rise to nonlinearities (with which we will not be concerned in this paper), as well as the familiar gyrokinetic drive associated with the equilibrium distribution $f_{0s}$![]() , viz.
, viz.
where
are the characteristic length scales associated with the radial equilibrium gradients of both density and temperature, respectively, $\eta _s$![]() is their ratio, and $x$
is their ratio, and $x$![]() is the direction of the equilibrium gradients. The magnetic drifts associated with the equilibrium field are
is the direction of the equilibrium gradients. The magnetic drifts associated with the equilibrium field are
The last term on the right-hand side of (2.3) is the (linearised) collision operator, which we henceforth neglect given that we are interested in studying collisionless dynamics. The electromagnetic fields appearing in the gyrokinetic equation (2.3) are determined by the quasineutrality condition
where $\left \langle \cdots \right \rangle _{\boldsymbol {r}}$![]() denotes the gyroaverage at constant $\boldsymbol {r}$
denotes the gyroaverage at constant $\boldsymbol {r}$![]() , and by the parallel and perpendicular parts of Ampère's law, which are respectively
, and by the parallel and perpendicular parts of Ampère's law, which are respectively

Together, (2.3) and (2.8)–(2.10) form a closed system of equations that, in principle, allows us to determine $h_s$![]() and thus the evolution of the fluctuations in our plasma. In this work, we solve the linear part of this system in the ‘local’ limit (Beer, Cowley & Hammett Reference Beer, Cowley and Hammett1995): we assume that the gradients of all equilibrium quantities are constant – including the geometric coefficients $\boldsymbol {b}_0\boldsymbol {\cdot }{\boldsymbol {\nabla }}\boldsymbol {b}_0$
and thus the evolution of the fluctuations in our plasma. In this work, we solve the linear part of this system in the ‘local’ limit (Beer, Cowley & Hammett Reference Beer, Cowley and Hammett1995): we assume that the gradients of all equilibrium quantities are constant – including the geometric coefficients $\boldsymbol {b}_0\boldsymbol {\cdot }{\boldsymbol {\nabla }}\boldsymbol {b}_0$![]() and ${\boldsymbol {\nabla }}\log B_0$
and ${\boldsymbol {\nabla }}\log B_0$![]() that appear in the magnetic drifts – and choose orthonormal coordinates $(x, y, z)$
that appear in the magnetic drifts – and choose orthonormal coordinates $(x, y, z)$![]() , in which $\hat {\boldsymbol {z}}=\boldsymbol {b}_0$
, in which $\hat {\boldsymbol {z}}=\boldsymbol {b}_0$![]() is the direction of the magnetic field, $\hat {\boldsymbol {x}}$
is the direction of the magnetic field, $\hat {\boldsymbol {x}}$![]() is, as above, the direction of the equilibrium gradients (cf. the radial direction in toroidal geometry), and $\hat {\boldsymbol {y}} \equiv \boldsymbol {b}_0 \times \hat {\boldsymbol {x}}$
is, as above, the direction of the equilibrium gradients (cf. the radial direction in toroidal geometry), and $\hat {\boldsymbol {y}} \equiv \boldsymbol {b}_0 \times \hat {\boldsymbol {x}}$![]() is the binormal direction (cf. the poloidal direction in toroidal geometry). One can think of this geometry as that of a $Z$
is the binormal direction (cf. the poloidal direction in toroidal geometry). One can think of this geometry as that of a $Z$![]() -pinch (see Ricci et al. Reference Ricci, Rogers, Dorland and Barnes2006; Ivanov et al. Reference Ivanov, Schekochihin, Dorland, Field and Parra2020; Adkins et al. Reference Adkins, Schekochihin, Ivanov and Roach2022; Ivanov, Schekochihin & Dorland Reference Ivanov, Schekochihin and Dorland2022) due to the assumption of constant magnetic curvature and lack of magnetic shear, which we have implicitly assumed. Under these assumptions, the system of (2.3), (2.8)–(2.10) is homogeneous in space, allowing us to impose periodic boundary conditions in all three spatial dimensions.
-pinch (see Ricci et al. Reference Ricci, Rogers, Dorland and Barnes2006; Ivanov et al. Reference Ivanov, Schekochihin, Dorland, Field and Parra2020; Adkins et al. Reference Adkins, Schekochihin, Ivanov and Roach2022; Ivanov, Schekochihin & Dorland Reference Ivanov, Schekochihin and Dorland2022) due to the assumption of constant magnetic curvature and lack of magnetic shear, which we have implicitly assumed. Under these assumptions, the system of (2.3), (2.8)–(2.10) is homogeneous in space, allowing us to impose periodic boundary conditions in all three spatial dimensions.
In the next section, we consider the time evolution of a single Fourier mode and obtain the resulting gyrokinetic dispersion relation.
2.2 Linear gyrokinetic problem
Neglecting the nonlinear term and introducing the spatial Fourier decomposition:
with $\boldsymbol {k} = \boldsymbol {k_\perp } + k_\parallel \boldsymbol {b}_0$![]() , the Fourier modes ${h_s}_{\boldsymbol {k}}$
, the Fourier modes ${h_s}_{\boldsymbol {k}}$![]() and ${\chi }_{\boldsymbol {k}}$
and ${\chi }_{\boldsymbol {k}}$![]() can be shown to satisfy
can be shown to satisfy
where we have defined the drift frequencies associated with the equilibrium gradients of species $s$![]() [cf. (2.5)]:
[cf. (2.5)]:
and with the equilibrium magnetic field curvature and gradient [cf. (2.7)]:

where
Starting from the perpendicular force balance of the gyrokinetic equilibrium [see (128) in Abel et al. Reference Abel, Plunk, Wang, Barnes, Cowley, Dorland and Schekochihin2013], it is straightforward to show that the difference between these two drifts is given by

where $\beta _s = 8 {\rm \pi}n_{0s} T_{0s}/B_0^2$![]() is the plasma beta of species $s$
is the plasma beta of species $s$![]() . Lastly, the gyroaveraged Fourier-transformed gyrokinetic potential is
. Lastly, the gyroaveraged Fourier-transformed gyrokinetic potential is
while the field equations (2.8)–(2.10) can be written as (see, e.g. Howes et al. Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006)


where $b_s = k_\perp v_\perp /\varOmega _s$![]() , and ${\rm J}_0$
, and ${\rm J}_0$![]() , ${\rm J}_1$
, ${\rm J}_1$![]() are the Bessel functions of the first kind (Abramowitz & Stegun Reference Abramowitz and Stegun1972) that capture finite-Larmor-radius effects. It will prove convenient to combine ${\phi }_{\boldsymbol {k}}$
are the Bessel functions of the first kind (Abramowitz & Stegun Reference Abramowitz and Stegun1972) that capture finite-Larmor-radius effects. It will prove convenient to combine ${\phi }_{\boldsymbol {k}}$![]() , $A_{\parallel \boldsymbol {k}}$
, $A_{\parallel \boldsymbol {k}}$![]() , and ${\delta \! B}_{\parallel \boldsymbol {k}}$
, and ${\delta \! B}_{\parallel \boldsymbol {k}}$![]() into a single vector $\boldsymbol {\chi }_{\boldsymbol {k}}$
into a single vector $\boldsymbol {\chi }_{\boldsymbol {k}}$![]() given by
given by

Here, and in what follows, we normalise the electromagnetic fields using an arbitrary reference mass $m_r$![]() , density $n_{0r}$
, density $n_{0r}$![]() , thermal velocity $v_{{\rm th}r}$
, thermal velocity $v_{{\rm th}r}$![]() , temperature $T_{0r}$
, temperature $T_{0r}$![]() , and gyroradius $\rho _r$
, and gyroradius $\rho _r$![]() .
.
Following Landau (Reference Landau1946), we consider an initial-value problem and introduce the Laplace transformations
Assuming there exist positive real $m$![]() and $M$
and $M$![]() such that
such that
for all $t > 0$![]() , and picking any real $\sigma$
, and picking any real $\sigma$![]() with $\sigma > m$
with $\sigma > m$![]() , the integrals in (2.22) converge and the transformed distributions ${\hat {h}}_{s \boldsymbol {k}}$
, the integrals in (2.22) converge and the transformed distributions ${\hat {h}}_{s \boldsymbol {k}}$![]() and fields $\hat {\boldsymbol {\chi }}_{\boldsymbol {k}}$
and fields $\hat {\boldsymbol {\chi }}_{\boldsymbol {k}}$![]() are analytic for all complex values of $p$
are analytic for all complex values of $p$![]() with $\mathrm {Re}(p) \geqslant \sigma$
with $\mathrm {Re}(p) \geqslant \sigma$![]() . The inverse transformations are given by
. The inverse transformations are given by
where the contour of integration ${C_\sigma }$![]() is along a straight line parallel to the imaginary axis and intersecting the real axis at $\mathrm {Re}(p) = \sigma$
is along a straight line parallel to the imaginary axis and intersecting the real axis at $\mathrm {Re}(p) = \sigma$![]() , as in figure 1 (this is the so-called Bromwich contour).
, as in figure 1 (this is the so-called Bromwich contour).

Figure 1. The complex $p$![]() plane, with $\mathrm {Re}(p)$
plane, with $\mathrm {Re}(p)$![]() and $\mathrm {Im}(p)$
and $\mathrm {Im}(p)$![]() shown on the horizontal and vertical axes, respectively. The contour of integration for the inverse Laplace transform ${C_\sigma }$
shown on the horizontal and vertical axes, respectively. The contour of integration for the inverse Laplace transform ${C_\sigma }$![]() is is a vertical straight line at $\mathrm {Re}(p) = \sigma$
is is a vertical straight line at $\mathrm {Re}(p) = \sigma$![]() , to the right of which (i.e. in the shaded grey region) the functions ${\hat {h}}_{s \boldsymbol {k}}$
, to the right of which (i.e. in the shaded grey region) the functions ${\hat {h}}_{s \boldsymbol {k}}$![]() and ${\hat {\chi }}_{\boldsymbol {k}}$
and ${\hat {\chi }}_{\boldsymbol {k}}$![]() are guaranteed to be analytic. Singularities, such as poles (indicated by crosses) or branch cuts (indicated by the zigzag line), could exist at $\mathrm {Re}(p) < \sigma$
are guaranteed to be analytic. Singularities, such as poles (indicated by crosses) or branch cuts (indicated by the zigzag line), could exist at $\mathrm {Re}(p) < \sigma$![]() .
.
Performing the Laplace transform as in (2.22), (2.12) straightforwardly becomes
where ${g}_{s \boldsymbol {k}}$![]() is the initial condition:
is the initial condition:
Then, normalising the characteristic frequencies to the parallel-streaming rateFootnote 1
and defining the dimensionless velocity variables
we substitute (2.25) into the Laplace transforms of the field equations (2.18)–(2.20) to obtain the linear eigenvalue problem
in which $\boldsymbol{\mathsf{L}} $![]() is the linear coefficient matrix and $\boldsymbol {G}$
is the linear coefficient matrix and $\boldsymbol {G}$![]() is the vector of the initial conditions of the fields. The components of $\boldsymbol{\mathsf{L}} $
is the vector of the initial conditions of the fields. The components of $\boldsymbol{\mathsf{L}} $![]() are given by
are given by




where we have defined the following integrals
Here, and throughout the remainder of this paper, the parameters $a$![]() and $b$
and $b$![]() are assumed to be both real and positive, ensuring integral convergence. Finally, the components of $\boldsymbol {G} = (G_\phi, G_A, G_B)^{\rm T}$
are assumed to be both real and positive, ensuring integral convergence. Finally, the components of $\boldsymbol {G} = (G_\phi, G_A, G_B)^{\rm T}$![]() are given by
are given by

The eigenvalue problem (2.29) can be inverted to solve for the fields in the usual way, viz.
where $\text {adj}\:\boldsymbol{\mathsf{L}}$![]() and $\det \boldsymbol{\mathsf{L}}$
and $\det \boldsymbol{\mathsf{L}}$![]() are the adjugate matrix and determinant of the linear matrix $\boldsymbol{\mathsf{L}}$
are the adjugate matrix and determinant of the linear matrix $\boldsymbol{\mathsf{L}}$![]() , respectively. The time-dependent fields are then determined by the inverse Laplace transform of (2.47). As discussed above, the integrals in (2.24) are, before analytic continuation, defined for $\mathrm {Re}(p) \geqslant \sigma > 0$
, respectively. The time-dependent fields are then determined by the inverse Laplace transform of (2.47). As discussed above, the integrals in (2.24) are, before analytic continuation, defined for $\mathrm {Re}(p) \geqslant \sigma > 0$![]() . For these values of $p$
. For these values of $p$![]() , $\mathrm {Im}(\zeta _s) > 0$
, $\mathrm {Im}(\zeta _s) > 0$![]() , and so the integrals in (2.39)–(2.43) converge and are analytic functions of $p$
, and so the integrals in (2.39)–(2.43) converge and are analytic functions of $p$![]() . Note that the equation
. Note that the equation
is commonly known as the ‘dispersion relation’, while we shall refer to $D$![]() itself as the ‘dispersion function’.
itself as the ‘dispersion function’.
2.3 Drift-kinetic limit
To evaluate the integrals (2.39)–(2.43), we specialise to the drift-kinetic limit, in which the perpendicular wavenumbers of the perturbations are assumed small in comparison to the species’ gyroradii, viz.
In this limit, the Bessel functions can be expanded as
meaning that, to leading order in $b_s$![]() , the contributions of the Bessel functions to the integrals (2.39)–(2.43) are equal to one, and we may write
, the contributions of the Bessel functions to the integrals (2.39)–(2.43) are equal to one, and we may write
where ${\rm I}_{a,b}^{(s)}$![]() and ${\rm J}_{a,b}^{(s)}$
and ${\rm J}_{a,b}^{(s)}$![]() are given by
are given by
Furthermore, we consider the particular case in which the difference between the curvature and ${\boldsymbol {\nabla }} \! B$![]() drifts, given by the right-hand side of (2.16) is zero and so their associated drift frequencies can be taken to be equal, viz.
drifts, given by the right-hand side of (2.16) is zero and so their associated drift frequencies can be taken to be equal, viz.
Note that neither approximation should be interpreted as a consequence of some asymptotic ordering of the parameters describing our gyrokinetic system of equations. Instead, they should be viewed as formal approximations that allow us to obtain a solvable case of a more general one. Their relaxation is discussed in § 7.
With these simplifications, we have reduced our problem to the evaluation of
where we have used (2.54) and have dropped the species index for the sake of compactness of notation.
3 Previous solutions
Before tackling the task of analytically integrating (2.55) and (2.56), we shall briefly discuss some special cases in which these expressions are already known within the literature. A reader already familiar with these solutions may wish to skip ahead to § 4, working backwards if further clarification is required.
3.1 The plasma dispersion function and Landau's solution
In the absence of magnetic drifts (i.e. when $\zeta _d = 0$![]() ), (2.55) and (2.56) can straight- forwardly be written in terms of the well-studied plasma dispersion function (Faddeeva & Terent'ev Reference Faddeeva and Terent'ev1954; Fried & Conte Reference Fried and Conte1961):
), (2.55) and (2.56) can straight- forwardly be written in terms of the well-studied plasma dispersion function (Faddeeva & Terent'ev Reference Faddeeva and Terent'ev1954; Fried & Conte Reference Fried and Conte1961):
where the integral is defined for $\mathrm {Im}(\zeta )>0$![]() with the integration contour along the real $u$
with the integration contour along the real $u$![]() axis, as in figure 2(a). In particular, we have that
axis, as in figure 2(a). In particular, we have that
where we have, for the sake of brevity, introduced the shorthand notation
The integral in (3.1) can be analytically continued to $\mathrm {Im}(\zeta ) \leqslant 0$![]() by deforming the contour of integration in such a way as to always keep the pole above it, as shown in figure 2(b, c). This is known as the Landau prescription, and the resultant contour is the well-known Landau contour $C_L$
by deforming the contour of integration in such a way as to always keep the pole above it, as shown in figure 2(b, c). This is known as the Landau prescription, and the resultant contour is the well-known Landau contour $C_L$![]() (Landau Reference Landau1946).
(Landau Reference Landau1946).

Figure 2. The Landau prescription for the contour of integration $C_L$![]() that gives the analytic continuation of (3.1). As the Laplace transform demands $\mathrm {Re}(p) \geqslant \sigma > 0$
that gives the analytic continuation of (3.1). As the Laplace transform demands $\mathrm {Re}(p) \geqslant \sigma > 0$![]() , the pole $u = \zeta$
, the pole $u = \zeta$![]() is located in the upper-half plane [where $\mathrm {Im}(\zeta ) > 0$
is located in the upper-half plane [where $\mathrm {Im}(\zeta ) > 0$![]() , see footnote 1], above the contour of integration, as in panel (a). Therefore, the appropriate analytic continuation for $\mathrm {Re}(p) \leqslant 0$
, see footnote 1], above the contour of integration, as in panel (a). Therefore, the appropriate analytic continuation for $\mathrm {Re}(p) \leqslant 0$![]() [i.e. $\mathrm {Im}(\zeta ) \leqslant 0$
[i.e. $\mathrm {Im}(\zeta ) \leqslant 0$![]() ] demands that the contour must be deformed so as to always remain below the pole, as in panels (b, c). Cauchy's integral theorem ensures that we are free to deform the contour without changing the value of the integral, so long as it does not cross the pole.
] demands that the contour must be deformed so as to always remain below the pole, as in panels (b, c). Cauchy's integral theorem ensures that we are free to deform the contour without changing the value of the integral, so long as it does not cross the pole.
The plasma dispersion function (3.1) is ubiquitous in calculations of linear waves and instabilities in systems with a spatially uniform magnetic field; notable examples include the electron-temperature-gradient (see, e.g. Liu Reference Liu1971; Lee et al. Reference Lee, Dong, Guzdar and Liu1987) and ion-temperature-gradient (see, e.g. Rudakov & Sagdeev Reference Rudakov and Sagdeev1961; Coppi et al. Reference Coppi, Furth, Rosenbluth and Sagdeev1966; Sauter, Vaclavik & Skiff Reference Sauter, Vaclavik and Skiff1990; Brunner & Vaclavik Reference Brunner and Vaclavik1998; Smolyakov, Yagi & Kishimoto Reference Smolyakov, Yagi and Kishimoto2002) instabilities, the latter of which we shall consider in § 8. It is also worth noting that the Bessel functions can easily be incorporated into the integrals if $\zeta _d=0$![]() because the resonant denominators are independent of $\mu$
because the resonant denominators are independent of $\mu$![]() . The resulting expressions involve modified Bessel functions and are well known in the literature (see, e.g. Howes et al. Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006).
. The resulting expressions involve modified Bessel functions and are well known in the literature (see, e.g. Howes et al. Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006).
3.2 Two-dimensional limit
In the 2-D limit, $k_\parallel \rightarrow 0$![]() with $\zeta \sim \zeta _d \rightarrow \infty$
with $\zeta \sim \zeta _d \rightarrow \infty$![]() , it can be shown (via, e.g. a partial-fractions expansion of the integrand) that (2.55) can be expressed exactly in terms of products of the plasma dispersion function (Biglari, Diamond & Rosenbluth Reference Biglari, Diamond and Rosenbluth1989), viz.
, it can be shown (via, e.g. a partial-fractions expansion of the integrand) that (2.55) can be expressed exactly in terms of products of the plasma dispersion function (Biglari, Diamond & Rosenbluth Reference Biglari, Diamond and Rosenbluth1989), viz.
with the integral for ${\rm J}_{a,b}$![]() vanishing to leading order because the integrand in (2.56) is manifestly odd in $u$
vanishing to leading order because the integrand in (2.56) is manifestly odd in $u$![]() in this limit. The analytic continuation for (3.4) is significantly more subtle than in the case of the plasma dispersion function (3.1), owing to the presence of the branch point at $\zeta = 0$
in this limit. The analytic continuation for (3.4) is significantly more subtle than in the case of the plasma dispersion function (3.1), owing to the presence of the branch point at $\zeta = 0$![]() ; we shall delay discussion of these subtleties until § 6. The solution (3.4) has been used extensively in the investigation of 2-D ITG instabilities (see, e.g. Similon et al. Reference Similon, Sedlak, Stotler, Berk, Horton and Choi1984; Biglari et al. Reference Biglari, Diamond and Rosenbluth1989; Kuroda et al. Reference Kuroda, Sugama, Kanno, Okamoto and Horton1998; Sugama Reference Sugama1999; Ricci et al. Reference Ricci, Rogers, Dorland and Barnes2006; Helander et al. Reference Helander, Mishchenko, Kleiber and Xanthopoulos2011; Mishchenko, Plunk & Helander Reference Mishchenko, Plunk and Helander2018; Zocco et al. Reference Zocco, Xanthopoulos, Doerk, Connor and Helander2018).
; we shall delay discussion of these subtleties until § 6. The solution (3.4) has been used extensively in the investigation of 2-D ITG instabilities (see, e.g. Similon et al. Reference Similon, Sedlak, Stotler, Berk, Horton and Choi1984; Biglari et al. Reference Biglari, Diamond and Rosenbluth1989; Kuroda et al. Reference Kuroda, Sugama, Kanno, Okamoto and Horton1998; Sugama Reference Sugama1999; Ricci et al. Reference Ricci, Rogers, Dorland and Barnes2006; Helander et al. Reference Helander, Mishchenko, Kleiber and Xanthopoulos2011; Mishchenko, Plunk & Helander Reference Mishchenko, Plunk and Helander2018; Zocco et al. Reference Zocco, Xanthopoulos, Doerk, Connor and Helander2018).
3.3 Numerical methods
Owing to their analytical complexity, previous literature has also been devoted to the numerical evaluation of (2.55) and (2.56) (see Beer & Hammett Reference Beer and Hammett1996; Gürcan Reference Gürcan2014; Gültekin & Gürcan Reference Gültekin and Gürcan2018; Gültekin & Gürcan Reference Gültekin and Gürcan2020; Parisi et al. Reference Parisi, Parra, Roach, Giroud, Dorland, Hatch, Barnes, Hillesheim, Aiba and Ball2020 and references contained therein). In many cases, this involves expressing these integrals in terms of one-dimensional integrals. For example, writing
allows the integration over $u$![]() and $\mu$
and $\mu$![]() in (2.55) and (2.56) to be done analytically, leaving an integral over $\lambda$
in (2.55) and (2.56) to be done analytically, leaving an integral over $\lambda$![]() that can be evaluated numerically (cf. Beer & Hammett Reference Beer and Hammett1996; Parisi et al. Reference Parisi, Parra, Roach, Giroud, Dorland, Hatch, Barnes, Hillesheim, Aiba and Ball2020). While this method is quite general – in that it also allows the direct inclusion of the Bessel functions in (2.39)–(2.43) – the numerical evaluation of the resultant expressions can often be slow, numerical errors may be difficult to quantify, and subtleties like multivaluedness and branch cuts easy to overlook. This motivates the goal of the present study, viz. to find expressions for these integrals in terms of known functions that can be better understood analytically and more readily computed numerically.
that can be evaluated numerically (cf. Beer & Hammett Reference Beer and Hammett1996; Parisi et al. Reference Parisi, Parra, Roach, Giroud, Dorland, Hatch, Barnes, Hillesheim, Aiba and Ball2020). While this method is quite general – in that it also allows the direct inclusion of the Bessel functions in (2.39)–(2.43) – the numerical evaluation of the resultant expressions can often be slow, numerical errors may be difficult to quantify, and subtleties like multivaluedness and branch cuts easy to overlook. This motivates the goal of the present study, viz. to find expressions for these integrals in terms of known functions that can be better understood analytically and more readily computed numerically.
4 The generalised plasma dispersion function
In this section, we detail the method by which (2.55) and (2.56) can be expressed in terms of the plasma dispersion function (3.1), making the resultant expressions simpler to treat both analytically and numerically. When solving the integrals, we will assume that $p$![]() remains within the region of analyticity $\mathrm {Re}(p) \geqslant \sigma > 0$
remains within the region of analyticity $\mathrm {Re}(p) \geqslant \sigma > 0$![]() , with $\sigma$
, with $\sigma$![]() defined after (2.23). The analytic continuation will be performed only after obtaining expressions for (2.55) and (2.56) in terms of known functions. In the main text, we present the integration of (2.55); all other required expressions follow directly from this single integral and have been relegated to appendices A and B due to their complexity. The remainder of this section proceeds as follows. Section 4.1 discusses the multivalued nature of the integrand of (2.55) before evaluating the integral over $u$
defined after (2.23). The analytic continuation will be performed only after obtaining expressions for (2.55) and (2.56) in terms of known functions. In the main text, we present the integration of (2.55); all other required expressions follow directly from this single integral and have been relegated to appendices A and B due to their complexity. The remainder of this section proceeds as follows. Section 4.1 discusses the multivalued nature of the integrand of (2.55) before evaluating the integral over $u$![]() in terms of plasma dispersion function (3.1), allowing us, in § 4.2, to obtain a closed form expression for (2.55) upon evaluating the remaining integral over $\mu$
in terms of plasma dispersion function (3.1), allowing us, in § 4.2, to obtain a closed form expression for (2.55) upon evaluating the remaining integral over $\mu$![]() . In § 4.3, we discuss how the $\partial _a$
. In § 4.3, we discuss how the $\partial _a$![]() and $\partial _b$
and $\partial _b$![]() derivatives of (2.55) and (2.56) can be obtained, with detailed calculations relegated to appendix B. Then, in § 4.4, we discuss some important properties of (2.55) and (2.56).
derivatives of (2.55) and (2.56) can be obtained, with detailed calculations relegated to appendix B. Then, in § 4.4, we discuss some important properties of (2.55) and (2.56).
4.1 Multivaluedness
To begin, it shall be useful to consider the integral over $u$![]() separately, and so we write (2.55) as follows:
separately, and so we write (2.55) as follows:
Now, for each value of $\mu$![]() , the denominator of $\tilde {{\rm I}}_{a}$
, the denominator of $\tilde {{\rm I}}_{a}$![]() has two zeros at
has two zeros at
that produce poles on opposite sides of the integration contour along the real $u$![]() axis. Unsurprisingly, given the presence of square roots in (4.2), $\tilde {{\rm I}}_{a}$
axis. Unsurprisingly, given the presence of square roots in (4.2), $\tilde {{\rm I}}_{a}$![]() is a multivalued function. In particular, we shall find that $\tilde {{\rm I}}_{a}$
is a multivalued function. In particular, we shall find that $\tilde {{\rm I}}_{a}$![]() , and thus ${\rm I}_{a,b}$
, and thus ${\rm I}_{a,b}$![]() , has two branches, just like the square root. To define these two branches, we need to choose a branch cut, which will allow us to ‘label’ the two zeros in (4.2). Note that this choice cannot (and does not) affect the time evolution of the potentials that results from the inverse Laplace transform of (2.21). It turns out to be analytically convenient to consider the ‘principal’ branch cut for the square-root function, for which $\sqrt {z}$
, has two branches, just like the square root. To define these two branches, we need to choose a branch cut, which will allow us to ‘label’ the two zeros in (4.2). Note that this choice cannot (and does not) affect the time evolution of the potentials that results from the inverse Laplace transform of (2.21). It turns out to be analytically convenient to consider the ‘principal’ branch cut for the square-root function, for which $\sqrt {z}$![]() is discontinuous across $\mathrm {Re}(z) < 0$
is discontinuous across $\mathrm {Re}(z) < 0$![]() . We can then define the two branches of the square root, $\sqrt [+]{z}$
. We can then define the two branches of the square root, $\sqrt [+]{z}$![]() and $\sqrt [-]{z}$
and $\sqrt [-]{z}$![]() , where the principal branch satisfies $\sqrt [+]{z} > 0$
, where the principal branch satisfies $\sqrt [+]{z} > 0$![]() for all positive real $z$
for all positive real $z$![]() , and $\mathrm {sgn}[\mathrm {Im} (\sqrt [+]{z})] = \mathrm {sgn}[\mathrm {Im}(z)]$
, and $\mathrm {sgn}[\mathrm {Im} (\sqrt [+]{z})] = \mathrm {sgn}[\mathrm {Im}(z)]$![]() .
.
At this point, it is non-trivial to define the second branch of ${\rm I}_{a,b}$![]() . The choice of a branch for the square root does not determine the branch of the integral (4.1) but only the labels of the zeros in (4.2) – observe that (4.1) makes no reference to any multivalued functions. Indeed, the function ${\rm I}_{a,b}$
. The choice of a branch for the square root does not determine the branch of the integral (4.1) but only the labels of the zeros in (4.2) – observe that (4.1) makes no reference to any multivalued functions. Indeed, the function ${\rm I}_{a,b}$![]() is defined as the integral in (4.1) only for ${\mathrm {Im}(\zeta ) > 0}$
is defined as the integral in (4.1) only for ${\mathrm {Im}(\zeta ) > 0}$![]() ; the multivaluedness becomes relevant after one considers the analytic continuation to $\mathrm {Im}(\zeta ) < 0$
; the multivaluedness becomes relevant after one considers the analytic continuation to $\mathrm {Im}(\zeta ) < 0$![]() . To make this explicit, until we perform said continuation, we will make use of the labels $\tilde {{\rm I}}_{a}^+$
. To make this explicit, until we perform said continuation, we will make use of the labels $\tilde {{\rm I}}_{a}^+$![]() and ${\rm I}_{a,b}^+$
and ${\rm I}_{a,b}^+$![]() to indicate that our expressions only apply to this one branch.
to indicate that our expressions only apply to this one branch.
Choosing to work with $\sqrt [+]{}$![]() , the zeros in (4.2) can be written as
, the zeros in (4.2) can be written as
Using a partial-fraction expansion of the integrand, it follows that

Now, given that $\mathrm {Im}(\zeta ) > 0$![]() , the sign of the imaginary part of $\sqrt [+]{1 + 8\zeta _d(\zeta - \zeta _d\mu )}$
, the sign of the imaginary part of $\sqrt [+]{1 + 8\zeta _d(\zeta - \zeta _d\mu )}$![]() is determined by the sign of $\zeta _d$
is determined by the sign of $\zeta _d$![]() , viz.
, viz.
and so (4.3) implies that $\mathrm {Im}(u_\pm ) > 0$![]() . Therefore, the first integral in the brackets in (4.4) is manifestly the plasma dispersion function, as the imaginary part of the pole at $u = u_-$
. Therefore, the first integral in the brackets in (4.4) is manifestly the plasma dispersion function, as the imaginary part of the pole at $u = u_-$![]() has the correct sign for the definition (3.1), i.e. $\mathrm {Im}(u_-) > 0$
has the correct sign for the definition (3.1), i.e. $\mathrm {Im}(u_-) > 0$![]() . The second integral has a pole at $u = -u_+$
. The second integral has a pole at $u = -u_+$![]() with the opposite sign of its imaginary part, i.e. $\mathrm {Im}(-u_+) < 0$
with the opposite sign of its imaginary part, i.e. $\mathrm {Im}(-u_+) < 0$![]() , meaning that it can also be turned into a plasma dispersion function under a straightforward change of variables $u \mapsto -u$
, meaning that it can also be turned into a plasma dispersion function under a straightforward change of variables $u \mapsto -u$![]() (this effectively flips the pole from being below the real $u$
(this effectively flips the pole from being below the real $u$![]() axis to being above it). Thus, it follows that (4.4) can be written as
axis to being above it). Thus, it follows that (4.4) can be written as
where we have used the shorthand notation (3.3) for $Z_a$![]() .
.
4.2 Explicit evaluation of ${\rm I}_{a,b}^+$
Using (4.6), our expression for ${\rm I}_{a,b}^+$![]() thus becomes:
thus becomes:
Using (4.3), together with the property $Z'(u) = -2 [1 + uZ(u)]$![]() , it can be deduced that
, it can be deduced that
and
It is then a matter of straightforward algebra to show that (4.7) can be rewritten as
Observe that (2.30)–(2.38) only reference ${\rm I}_{a,b}$![]() , and its derivatives with respect to $a$
, and its derivatives with respect to $a$![]() and $b$
and $b$![]() , evaluated at $a = b = 1$
, evaluated at $a = b = 1$![]() . We thus set $a=b$
. We thus set $a=b$![]() in (4.10) and, noting that $Z_a(u_\pm ) \to 0$
in (4.10) and, noting that $Z_a(u_\pm ) \to 0$![]() as $\mu \to \infty$
as $\mu \to \infty$![]() since $\mathrm {Im}(u_\pm ) > 0$
since $\mathrm {Im}(u_\pm ) > 0$![]() , we find
, we find
where we have introduced
From (4.11) and (4.12), it is clear that ${\rm I}_{a,a}$![]() is a multivalued function with a branch point at $\zeta = -1/8\zeta _d$
is a multivalued function with a branch point at $\zeta = -1/8\zeta _d$![]() . Its second branch can be obtained by considering the $\sqrt [-]{}$
. Its second branch can be obtained by considering the $\sqrt [-]{}$![]() branch of the square root in (4.12). This means that both branches can be summarised by defining
branch of the square root in (4.12). This means that both branches can be summarised by defining
where $\lambda = \pm$![]() labels the branch. Therefore, ${\rm I}_{a,a}$
labels the branch. Therefore, ${\rm I}_{a,a}$![]() can be written as
can be written as
Equation (4.14) is the key result of this paper. We shall henceforth refer to it as the generalised plasma dispersion function, in that it is the generalisation of the usual plasma dispersion function (3.1) to include the resonances associated with the magnetic drifts arising in a non-uniform magnetic field. In § 5.1, we show that, in the appropriate limits, the generalised plasma dispersion function reduces to the already-known solutions discussed in § 3. It is worth stressing that (4.14) is an exact result: no approximations have been made in deriving it from (2.55). Furthermore, the fact that (4.14) is composed of a product of plasma dispersion functions, for the evaluation of which there are numerous efficient algorithms, means that it is very fast to evaluate numerically. In § 5.2, we compare our expression for ${\rm I}_{a,b}$![]() with the numerical solver of Gürcan (Reference Gürcan2014).
with the numerical solver of Gürcan (Reference Gürcan2014).
It can be shown, via a similar procedure to that used to obtain (4.10) (see appendix A), that the related integral ${\rm J}_{a,b}^+$![]() (2.56) can be expressed exactly in terms of ${\rm I}_{a,b}^{+}$
(2.56) can be expressed exactly in terms of ${\rm I}_{a,b}^{+}$![]() and plasma dispersion functions as
and plasma dispersion functions as
and so
It is crucial to realise that the $\lambda =+$![]() branch of the functions ${\rm I}_{a,a}^{\lambda }$
branch of the functions ${\rm I}_{a,a}^{\lambda }$![]() and ${\rm J}_{a,a}^{\lambda }$
and ${\rm J}_{a,a}^{\lambda }$![]() is the ‘more important’ one, in the sense that it is the branch that is equal to the integrals (2.55) and (2.56) for $\mathrm {Im}(\zeta ) > 0$
is the ‘more important’ one, in the sense that it is the branch that is equal to the integrals (2.55) and (2.56) for $\mathrm {Im}(\zeta ) > 0$![]() . Thus, it is also the branch that is used in the inverse Laplace transform over ${C_\sigma }$
. Thus, it is also the branch that is used in the inverse Laplace transform over ${C_\sigma }$![]() , as in (2.24). Therefore, we shall refer to the $\lambda =+1$
, as in (2.24). Therefore, we shall refer to the $\lambda =+1$![]() branch as the ‘principal’ branch of ${\rm I}_{a,a}^{\lambda }$
branch as the ‘principal’ branch of ${\rm I}_{a,a}^{\lambda }$![]() and ${\rm J}_{a,a}^{\lambda }$
and ${\rm J}_{a,a}^{\lambda }$![]() .
.
4.3 Derivatives of the generalised plasma dispersion function
In addition to (2.55) and (2.56), the matrix elements (2.30)–(2.38) require the partial derivatives of these expressions with respect to $a$![]() and $b$
and $b$![]() . There are two factors that conspire to simplify the necessary calculations. First, we only need ${\rm I}_{a,b}$
. There are two factors that conspire to simplify the necessary calculations. First, we only need ${\rm I}_{a,b}$![]() , ${\rm J}_{a,b}$
, ${\rm J}_{a,b}$![]() and their derivatives at $a=b=1$
and their derivatives at $a=b=1$![]() . Second, the derivatives $\partial _a$
. Second, the derivatives $\partial _a$![]() and $\partial _b$
and $\partial _b$![]() often appear in the combination $\partial _a + \partial _b$
often appear in the combination $\partial _a + \partial _b$![]() . Notice that, by the chain rule,
. Notice that, by the chain rule,
for any (appropriately smooth) function $f$![]() . Using this, we can rewrite (2.30)–(2.38) in a way that involves only ${\rm I}_{a, a}$
. Using this, we can rewrite (2.30)–(2.38) in a way that involves only ${\rm I}_{a, a}$![]() , ${\rm J}_{a, a}$
, ${\rm J}_{a, a}$![]() , $\partial _a {\rm I}_{a,b}\vert _{a=b}$
, $\partial _a {\rm I}_{a,b}\vert _{a=b}$![]() , $\partial _b {\rm I}_{a,b}\vert _{a=b}$
, $\partial _b {\rm I}_{a,b}\vert _{a=b}$![]() , $\partial _b^2 {\rm I}_{a,b}\vert _{a=b}$
, $\partial _b^2 {\rm I}_{a,b}\vert _{a=b}$![]() , and $\partial _b {\rm J}_{a,b}\vert _{a=b}$
, and $\partial _b {\rm J}_{a,b}\vert _{a=b}$![]() . For example,
. For example,
where we have also taken advantage of (2.51). Due to their unwieldy length, the calculations of the required derivatives of ${\rm I}_{a,b}$![]() and ${\rm J}_{a,b}$
and ${\rm J}_{a,b}$![]() are relegated to appendix B.
are relegated to appendix B.
4.4 Branches of the dispersion function
Our choice of the principal branch cut for the square root gives the branches of the dispersion function $D$![]() (see § 2.2) several nice properties stemming from the relationship $\sqrt [+]{z^*} = \sqrt [+]{z}^*$
(see § 2.2) several nice properties stemming from the relationship $\sqrt [+]{z^*} = \sqrt [+]{z}^*$![]() for any complex $z$
for any complex $z$![]() . In appendix C, we show that ${\rm I}_{a, a}$
. In appendix C, we show that ${\rm I}_{a, a}$![]() and ${\rm J}_{a, a}$
and ${\rm J}_{a, a}$![]() satisfy
satisfy
and
Relations (4.19)–(4.22) are also valid for the $a$![]() and $b$
and $b$![]() derivatives of ${\rm I}_{a,b}$
derivatives of ${\rm I}_{a,b}$![]() and ${\rm J}_{a,b}$
and ${\rm J}_{a,b}$![]() . Of course, the functions ${\rm I}_{a,b}$
. Of course, the functions ${\rm I}_{a,b}$![]() and ${\rm J}_{a,b}$
and ${\rm J}_{a,b}$![]() are double-valued for each of the species $s$
are double-valued for each of the species $s$![]() , and so the dispersion function $D$
, and so the dispersion function $D$![]() has $2^{N}$
has $2^{N}$![]() branches for a system with $N$
branches for a system with $N$![]() species. Letting $\boldsymbol {\lambda } \equiv (\lambda _1, \lambda _2,\ldots, \lambda _N)$
species. Letting $\boldsymbol {\lambda } \equiv (\lambda _1, \lambda _2,\ldots, \lambda _N)$![]() be the vector of choices of the branch for each species, we can prove that $D$
be the vector of choices of the branch for each species, we can prove that $D$![]() satisfies (see appendix C)
satisfies (see appendix C)
These imply two different pairings of roots of the dispersion relation (2.48); see figures 11 and 12 in appendix C for a visual illustration of (4.23) and (4.24). Note that when using the superscript $\boldsymbol {\lambda }$![]() , we are referring to a particular branch, while without it, $D$
, we are referring to a particular branch, while without it, $D$![]() refers to all branches simultaneously.
refers to all branches simultaneously.
Equation (4.23) implies that solutions to the dispersion relation, i.e. $D=0$![]() , come in pairs $(p, k_y) \leftrightarrow (p^*, -k_y)$
, come in pairs $(p, k_y) \leftrightarrow (p^*, -k_y)$![]() , which is the condition for the fields $\phi$
, which is the condition for the fields $\phi$![]() , $A_\parallel$
, $A_\parallel$![]() , and $\delta B_\parallel$
, and $\delta B_\parallel$![]() to remain real for all $t$
to remain real for all $t$![]() . Therefore, such a pairing is bound to exist for all roots of $D = 0$
. Therefore, such a pairing is bound to exist for all roots of $D = 0$![]() , i.e. when all branches are considered. The choice of the principal branch of the square root makes this pairing also valid within each individual branch of $D$
, i.e. when all branches are considered. The choice of the principal branch of the square root makes this pairing also valid within each individual branch of $D$![]() , hence justifying our adoption of it in § 4.1. In § 6, we shall see that there is a better choice of branch for the purposes of performing the inverse Laplace transform.
, hence justifying our adoption of it in § 4.1. In § 6, we shall see that there is a better choice of branch for the purposes of performing the inverse Laplace transform.
Additionally, (4.24) says that if $p$![]() is a solution to $D=0$
is a solution to $D=0$![]() for a given poloidal wavenumber $k_y$
for a given poloidal wavenumber $k_y$![]() , then so is $-p^*$
, then so is $-p^*$![]() for the same $k_y$
for the same $k_y$![]() but for a different branch. At first glance, this might seem to imply that solutions to (2.48) always come in pairs, one stable and one unstable. While this is true if all branches of $D$
but for a different branch. At first glance, this might seem to imply that solutions to (2.48) always come in pairs, one stable and one unstable. While this is true if all branches of $D$![]() are considered, the time evolution given by the inverse Laplace transform (2.24) does not necessarily pick up contributions from all solutions to $D=0$
are considered, the time evolution given by the inverse Laplace transform (2.24) does not necessarily pick up contributions from all solutions to $D=0$![]() ; one cannot mix-and-match roots from different branches at will. In § 6, we shall see that the roots of (2.48) picked up by (2.24) depend on the choice of branch cut. However, only the principal branch, given by $\boldsymbol {\lambda } = (+, +,\ldots, +)$
; one cannot mix-and-match roots from different branches at will. In § 6, we shall see that the roots of (2.48) picked up by (2.24) depend on the choice of branch cut. However, only the principal branch, given by $\boldsymbol {\lambda } = (+, +,\ldots, +)$![]() , contributes linearly unstable solutions.
, contributes linearly unstable solutions.
5 Comparison with known results
5.1 Asymptotic expansions of ${\rm I}_{a,b}$
Let us now show that (4.14) asymptotes to the known limits discussed in § 3, as it should. First, in the limit of $\zeta _d \to 0$![]() , i.e. the limit of vanishing magnetic curvature, we employ the expansions
, i.e. the limit of vanishing magnetic curvature, we employ the expansions
and the asymptotic form $Z(\zeta ) \sim -\zeta ^{-1}$![]() for finite $\mathrm {Im}(\zeta )$
for finite $\mathrm {Im}(\zeta )$![]() but $|\mathrm {Re}(\zeta )| \to \infty$
but $|\mathrm {Re}(\zeta )| \to \infty$![]() , to find
, to find
Therefore, in the limit $\zeta _d \to 0$![]() , the principal branch satisfies
, the principal branch satisfies
in agreement with (3.2). This is visualised in figure 3. One can perform an analogous calculation with ${\rm J}_{a,b}^+$![]() to obtain the second expression in (3.2). Note that the second branch satisfies
to obtain the second expression in (3.2). Note that the second branch satisfies
in the limit $\zeta _d \to 0$![]() , which is not related to the correct expression for ${\rm I}_{a, a}$
, which is not related to the correct expression for ${\rm I}_{a, a}$![]() at zero magnetic curvature. The ‘connection’ between the two branches, viz. the branch cut, is ‘sent to infinity’ as $\zeta _d \to 0$
at zero magnetic curvature. The ‘connection’ between the two branches, viz. the branch cut, is ‘sent to infinity’ as $\zeta _d \to 0$![]() (see figure 3), and so the second branch ${\rm I}_{a, a}^-$
(see figure 3), and so the second branch ${\rm I}_{a, a}^-$![]() is ‘lost’ in the limit of zero magnetic curvature. In this way, the dispersion function loses all but one of its branches and becomes single-valued.
is ‘lost’ in the limit of zero magnetic curvature. In this way, the dispersion function loses all but one of its branches and becomes single-valued.

Figure 3. A plot of the principal branch ${\rm I}^+_{1,1}(\zeta, \zeta _d)$![]() in the complex plane for decreasing values of $\zeta _d$
in the complex plane for decreasing values of $\zeta _d$![]() (from left to right). The black cross denotes the branch point $\zeta = -1/8\zeta _d$
(from left to right). The black cross denotes the branch point $\zeta = -1/8\zeta _d$![]() . Panel (d) shows ${\rm I}_{1,1}^+(\zeta, 0) = Z(\zeta )$
. Panel (d) shows ${\rm I}_{1,1}^+(\zeta, 0) = Z(\zeta )$![]() . As $\zeta _d \to 0^+$
. As $\zeta _d \to 0^+$![]() , the branch point, alongside the entire branch cut, is pushed towards $\mathrm {Re}(\zeta ) \to -\infty$
, the branch point, alongside the entire branch cut, is pushed towards $\mathrm {Re}(\zeta ) \to -\infty$![]() . If $\zeta _d$
. If $\zeta _d$![]() were negative, the branch cut would instead join the branch point with $\mathrm {Re}(\zeta )\to +\infty$
were negative, the branch cut would instead join the branch point with $\mathrm {Re}(\zeta )\to +\infty$![]() , to which the branch cut would be pushed in the limit of $\zeta _d\to 0^-$
, to which the branch cut would be pushed in the limit of $\zeta _d\to 0^-$![]() .
.
Similarly, the 2-D limit can be found by taking the limit $\zeta \sim \zeta _d\to \infty$![]() , which is equivalent to dropping the $u$
, which is equivalent to dropping the $u$![]() term from the denominators in (2.55) and (2.56). In this case,
term from the denominators in (2.55) and (2.56). In this case,

and so one obtains (3.4).
Figure 4 compares the exact expressions (4.14) and (4.16) with their known asymptotic limits in the case of vanishing magnetic drifts (3.2) and 2-D perturbations (3.4), respectively. It is evident that, while these known asymptotic limits are obtained in the cases of small and large $\zeta _d$![]() , they are not a good approximation of ${\rm I}_{a,b}$
, they are not a good approximation of ${\rm I}_{a,b}$![]() and ${\rm J}_{a,b}$
and ${\rm J}_{a,b}$![]() for $\zeta _d\sim 1$
for $\zeta _d\sim 1$![]() , as one would expect.
, as one would expect.

Figure 4. Plots of the asymptotic convergence of ${\rm I}_{a,b}$![]() and ${\rm J}_{a,b}$
and ${\rm J}_{a,b}$![]() to their known limits. Panels (a, b) demonstrate the convergence of ${\rm I}_{1,1}^+$
to their known limits. Panels (a, b) demonstrate the convergence of ${\rm I}_{1,1}^+$![]() and ${\rm J}_{1,1}^+$
and ${\rm J}_{1,1}^+$![]() , given by (4.14) and (4.16), to their small- and large-$\zeta _d$
, given by (4.14) and (4.16), to their small- and large-$\zeta _d$![]() limits, given by (3.2) and (3.4), respectively. We define the relative difference of two functions $f$
limits, given by (3.2) and (3.4), respectively. We define the relative difference of two functions $f$![]() and $g$
and $g$![]() as $|f-g|/\min \{|f|, |g|\}$
as $|f-g|/\min \{|f|, |g|\}$![]() . Note that this is ill-defined if one of the functions is identically zero, so for the ${\rm J}_{1,1}$
. Note that this is ill-defined if one of the functions is identically zero, so for the ${\rm J}_{1,1}$![]() comparison in panel (b), we plot simply $|{\rm J}_{1,1}|$
comparison in panel (b), we plot simply $|{\rm J}_{1,1}|$![]() because we expect to recover ${\rm J}_{1,1} = 0$
because we expect to recover ${\rm J}_{1,1} = 0$![]() in the 2-D limit (3.4). The solid and dotted lines in panels (a, b) show the average and maximum relative difference, respectively, as computed over a grid of $32\times 32$
in the 2-D limit (3.4). The solid and dotted lines in panels (a, b) show the average and maximum relative difference, respectively, as computed over a grid of $32\times 32$![]() points for $\zeta$
points for $\zeta$![]() , equally spaced in $\mathrm {Re}(\zeta ) \in [1, 1]$
, equally spaced in $\mathrm {Re}(\zeta ) \in [1, 1]$![]() , $\mathrm {Im}(\zeta ) \in [0, 1]$
, $\mathrm {Im}(\zeta ) \in [0, 1]$![]() , for each value of $\zeta _d$
, for each value of $\zeta _d$![]() . Panel (c) demonstrates the convergence of the real (dashed) and imaginary (dash–dotted) parts of ${\rm I}_{1,1}^+$
. Panel (c) demonstrates the convergence of the real (dashed) and imaginary (dash–dotted) parts of ${\rm I}_{1,1}^+$![]() to the small- and large-$\zeta _d$
to the small- and large-$\zeta _d$![]() limits for a fixed $\zeta = 1+{\rm i}$
limits for a fixed $\zeta = 1+{\rm i}$![]() , which are given by $Z(\zeta )$
, which are given by $Z(\zeta )$![]() and $-Z^2(\sqrt {\varOmega })/\zeta _d$
and $-Z^2(\sqrt {\varOmega })/\zeta _d$![]() , with $\varOmega = \zeta /2\zeta _d$
, with $\varOmega = \zeta /2\zeta _d$![]() , respectively.
, respectively.
5.2 Numerical comparison with Gürcan (Reference Gürcan2014)
Gürcan (Reference Gürcan2014) consider a very similar problem to that on which this paper has focused but from a numerical perspective. In particular, they discuss the numerical integration of the function

defined for $\mathrm {Im}(\zeta _\alpha ) > 0$![]() , real $\zeta _\beta$
, real $\zeta _\beta$![]() and $b$
and $b$![]() , and $n>1$
, and $n>1$![]() . With a few algebraic manipulations, it can be shown that, for odd $n$
. With a few algebraic manipulations, it can be shown that, for odd $n$![]() ,
,

The above expression is actually correct only for $\zeta _d < 0$![]() , otherwise (5.7) computes the second ($\lambda = -$
, otherwise (5.7) computes the second ($\lambda = -$![]() ) branch of ${\rm I}_{a,b}$
) branch of ${\rm I}_{a,b}$![]() , ${\rm J}_{a,b}$
, ${\rm J}_{a,b}$![]() and their derivatives. In the case $\zeta _d < 0$
and their derivatives. In the case $\zeta _d < 0$![]() , the requirement $\mathrm {Im}(\zeta _\alpha ) > 0$
, the requirement $\mathrm {Im}(\zeta _\alpha ) > 0$![]() implies that $\mathrm {Im}(\zeta ) > 0$
implies that $\mathrm {Im}(\zeta ) > 0$![]() . Figure 5 shows a comparison between the values obtained via the results of this work [represented by (4.14), (4.16), (B12)–(B15)] and the Gürcan (Reference Gürcan2014) result (5.7) in the region $\mathrm {Re}(\zeta )\in [-10, 10]$
. Figure 5 shows a comparison between the values obtained via the results of this work [represented by (4.14), (4.16), (B12)–(B15)] and the Gürcan (Reference Gürcan2014) result (5.7) in the region $\mathrm {Re}(\zeta )\in [-10, 10]$![]() , $\mathrm {Im}(\zeta )\in [0, 10]$
, $\mathrm {Im}(\zeta )\in [0, 10]$![]() , ${\zeta _d \in [-10, -0.001]}$
, ${\zeta _d \in [-10, -0.001]}$![]() . There is good agreement for all tested values of $\zeta$
. There is good agreement for all tested values of $\zeta$![]() and $\zeta _d$
and $\zeta _d$![]() , with less than $1\,\%$
, with less than $1\,\%$![]() relative difference in most cases. It is important to stress that as our solution uses only standard functions, e.g. the plasma dispersion function $Z$
relative difference in most cases. It is important to stress that as our solution uses only standard functions, e.g. the plasma dispersion function $Z$![]() and $\sqrt {}$
and $\sqrt {}$![]() , for which there exist very efficient numerical algorithms. We found that even a naïve, unoptimised Python implementation took anywhere between $20$
, for which there exist very efficient numerical algorithms. We found that even a naïve, unoptimised Python implementation took anywhere between $20$![]() and $80$
and $80$![]() times less time to compute ${\rm I}_{a,b}$
times less time to compute ${\rm I}_{a,b}$![]() , ${\rm J}_{a,b}$
, ${\rm J}_{a,b}$![]() and their derivatives than the direct numerical integration of (5.7) implemented in Fortran at https://github.com/gurcani/zpdgen.
and their derivatives than the direct numerical integration of (5.7) implemented in Fortran at https://github.com/gurcani/zpdgen.

Figure 5. Mean (solid) and maximum (dotted) relative difference (defined as in figure 4) between expressions (4.14), (4.16), (B12)–(B15) and their equivalents derived from (5.8), computed via the code published at https://github.com/gurcani/zpdgen. For each $\zeta _d$![]() , we evaluated the respective functions at an equally spaced grid of $32\times 32$
, we evaluated the respective functions at an equally spaced grid of $32\times 32$![]() points in the region ${\mathrm {Re}(\zeta )\in [-10, 10]}$
points in the region ${\mathrm {Re}(\zeta )\in [-10, 10]}$![]() , $\mathrm {Im}(\zeta )\in [0, 10]$
, $\mathrm {Im}(\zeta )\in [0, 10]$![]() .
.
6 Analytic continuation for the inverse Laplace transform
Together, the expressions (4.14) and (4.16) for ${\rm I}_{a,a}$![]() and ${\rm J}_{a,a}$
and ${\rm J}_{a,a}$![]() , respectively, along with the derivatives (B12)–(B15), allow us to calculate $\boldsymbol{\mathsf{L}}$
, respectively, along with the derivatives (B12)–(B15), allow us to calculate $\boldsymbol{\mathsf{L}}$![]() and hence the Laplace-transformed fields (2.47). Recall that to determine the evolution of the system as a function of time, we need to compute the inverse Laplace transform
and hence the Laplace-transformed fields (2.47). Recall that to determine the evolution of the system as a function of time, we need to compute the inverse Laplace transform
where the contour of integration ${C_\sigma }$![]() is once again as in figure 1, and we remind the reader that $\hat {\boldsymbol {\chi }}_{\boldsymbol {k}}(p)$
is once again as in figure 1, and we remind the reader that $\hat {\boldsymbol {\chi }}_{\boldsymbol {k}}(p)$![]() is given by
is given by
where the vector of initial conditions $\boldsymbol {G}$![]() is given by (2.44)–(2.46).
is given by (2.44)–(2.46).
The results of § 4.2 show that the entries of $\boldsymbol{\mathsf{L}}$![]() have branch points at $\zeta _s = -1/8\zeta _{ds}$
have branch points at $\zeta _s = -1/8\zeta _{ds}$![]() , or equivalently, at $p = p_s$
, or equivalently, at $p = p_s$![]() , where
, where
but are otherwise free of poles since, apart from the square roots and the associated branch cuts, they are composed of entire functions. Recall that we have defined the branches of the dispersion function $D$![]() using the principal branch of the square root in (4.3). Therefore, the relevant branch $D^{\boldsymbol {\lambda }}$
using the principal branch of the square root in (4.3). Therefore, the relevant branch $D^{\boldsymbol {\lambda }}$![]() that enters the inverse Laplace transform is the principal branch given by $\boldsymbol {\lambda } = (+,\ldots, +)$
that enters the inverse Laplace transform is the principal branch given by $\boldsymbol {\lambda } = (+,\ldots, +)$![]() . This has branch cuts that connect the branch points $\zeta _s = -1/8\zeta _{ds}$
. This has branch cuts that connect the branch points $\zeta _s = -1/8\zeta _{ds}$![]() to $\zeta _s \to -\mathrm {sgn}(\zeta _{ds}) \infty$
to $\zeta _s \to -\mathrm {sgn}(\zeta _{ds}) \infty$![]() , or, equivalently, $p = p_s$
, or, equivalently, $p = p_s$![]() to $p \to {\rm i}\mathrm {sgn}(\zeta _{ds})\infty$
to $p \to {\rm i}\mathrm {sgn}(\zeta _{ds})\infty$![]() . While this choice of the principal branch and branch cuts was convenient for obtaining the closed forms of ${\rm I}_{a,b}$
. While this choice of the principal branch and branch cuts was convenient for obtaining the closed forms of ${\rm I}_{a,b}$![]() , ${\rm J}_{a,b}$
, ${\rm J}_{a,b}$![]() , and $D$
, and $D$![]() , and their properties, it is not necessarily the best one for performing the inverse Laplace transform (6.1). Instead, we would like to rotate the branch cuts by $\mathrm {sgn}(\zeta _{ds}) {\rm \pi}/2$
, and their properties, it is not necessarily the best one for performing the inverse Laplace transform (6.1). Instead, we would like to rotate the branch cuts by $\mathrm {sgn}(\zeta _{ds}) {\rm \pi}/2$![]() around $p_s$
around $p_s$![]() , so that they are parallel to the real $p$
, so that they are parallel to the real $p$![]() axis, as shown in figure 6. Let us call the branch $\mathcal {D}$
axis, as shown in figure 6. Let us call the branch $\mathcal {D}$![]() of the dispersion function obtained this way the ‘dispersion’ branch. Crucially, the rotation of the branch cuts does not disturb the values of the dispersion function at $\mathrm {Re}(p) > 0$
of the dispersion function obtained this way the ‘dispersion’ branch. Crucially, the rotation of the branch cuts does not disturb the values of the dispersion function at $\mathrm {Re}(p) > 0$![]() . Therefore, $\mathcal {D}(p) = D^{(+,\ldots +)}(p)$
. Therefore, $\mathcal {D}(p) = D^{(+,\ldots +)}(p)$![]() for $\mathrm {Re}(p) > 0$
for $\mathrm {Re}(p) > 0$![]() . This ensures that the ‘unphysical’ unstable zeros of the other branches of the dispersion function, which are a consequence of (4.24), do not contribute to the solution (see also discussion in § 4.4); the only unstable solutions that are picked up by the inverse Laplace transform are those of the principal branch.
. This ensures that the ‘unphysical’ unstable zeros of the other branches of the dispersion function, which are a consequence of (4.24), do not contribute to the solution (see also discussion in § 4.4); the only unstable solutions that are picked up by the inverse Laplace transform are those of the principal branch.

Figure 6. This diagram shows the ‘principal’ (in blue) and ‘dispersion’ (in black) branch cuts for a plasma with one negatively and one positively charged species, labelled as $s_1$![]() and $s_2$
and $s_2$![]() , respectively.
, respectively.
With this choice for the branch cuts of the dispersion function, we are ready to perform the inverse Laplace transform (6.1). This is done in the usual way, viz. by pushing the integration contour ${C_\sigma }$![]() towards $\mathrm {Re}(p) \to -\infty$
towards $\mathrm {Re}(p) \to -\infty$![]() , with the proviso that it must be deformed so as not to cross any singularities, e.g. poles or branch cuts. Pushing the contour to the vertical line at $\mathrm {Re}(p) = \rho$
, with the proviso that it must be deformed so as not to cross any singularities, e.g. poles or branch cuts. Pushing the contour to the vertical line at $\mathrm {Re}(p) = \rho$![]() , we find the new integration contour ${C_\rho }$
, we find the new integration contour ${C_\rho }$![]() (see figure 7). Since there are no singularities between ${C_\sigma }$
(see figure 7). Since there are no singularities between ${C_\sigma }$![]() and ${C_\rho }$
and ${C_\rho }$![]() , Cauchy's integral theorem ensures that the integrals over these two contours are equal. Taking the limit of $\rho \to -\infty$
, Cauchy's integral theorem ensures that the integrals over these two contours are equal. Taking the limit of $\rho \to -\infty$![]() , it is evident that the contributions arising from the vertical segments of ${C_\rho }$
, it is evident that the contributions arising from the vertical segments of ${C_\rho }$![]() are exponentially small [they are exponentially small at any $t > 0$
are exponentially small [they are exponentially small at any $t > 0$![]() because the integrand of the inverse Laplace transformation (2.24) contains a factor ${\rm e}^{\rho t}$
because the integrand of the inverse Laplace transformation (2.24) contains a factor ${\rm e}^{\rho t}$![]() ], while those arising from the integration along the horizontal segments leading towards and away from the poles cancel, leaving the contributions from the poles. The integration around the branch cuts is more subtle and will be discussed shortly.
], while those arising from the integration along the horizontal segments leading towards and away from the poles cancel, leaving the contributions from the poles. The integration around the branch cuts is more subtle and will be discussed shortly.

Figure 7. Same as in figure 1, except that the contour associated with the inverse Laplace transformation (6.1) has now been shifted to $\mathrm {Re}(p) = \rho$![]() , deforming it such that it does not cross any of the poles or the branch cut. We denote this new contour ${C_\rho }$
, deforming it such that it does not cross any of the poles or the branch cut. We denote this new contour ${C_\rho }$![]() . The original contour is shown by the vertical dashed line. The integrals along ${C_\sigma }$
. The original contour is shown by the vertical dashed line. The integrals along ${C_\sigma }$![]() and ${C_\rho }$
and ${C_\rho }$![]() are equal by Cauchy's integral theorem.
are equal by Cauchy's integral theorem.
There are several singularities present in (6.2) and hence in the integrand in (6.1). The first is the so-called ‘ballistic response’ associated with the initial conditions contained within $\boldsymbol {G}$![]() , arising from simple poles located along $\mathrm {Re}(p) = 0$
, arising from simple poles located along $\mathrm {Re}(p) = 0$![]() , viz.
, viz.
where we have assumed that ${g}_{s \boldsymbol {k}}$![]() is a smooth function. Plugging this into (2.44)–(2.46), we find that the contribution to $\boldsymbol {\chi }_{\boldsymbol {k}}(t)$
is a smooth function. Plugging this into (2.44)–(2.46), we find that the contribution to $\boldsymbol {\chi }_{\boldsymbol {k}}(t)$![]() due to the ballistic response can be written as
due to the ballistic response can be written as

There is a wealth of interesting physics that can arise from the ballistic response, see, e.g. Ewart et al. (Reference Ewart, Brown, Adkins and Schekochihin2022) and references therein, in the context of the Vlasov–Poisson system. However, this is not the focus of the present work and so will not be discussed further.
Another source of non-analyticity are the solutions to the dispersion relation $\mathcal {D} = 0$![]() , should any of these exist. The contributions to (6.1) arising from the zeros $p = p_j$
, should any of these exist. The contributions to (6.1) arising from the zeros $p = p_j$![]() of $\mathcal {D}$
of $\mathcal {D}$![]() can be written as
can be written as
It is evident that unlike the ballistic response, whose time dependence is an oscillating exponential, the terms (6.6) can, in general, be exponentially decaying (i.e. stable) for $\mathrm {Re}(p_j) < 0$![]() or growing (i.e. unstable) for $\mathrm {Re}(p_j) > 0$
or growing (i.e. unstable) for $\mathrm {Re}(p_j) > 0$![]() .
.
Finally, singularities may arise from the functions (2.39)–(2.43) that are contained within both $\text {adj}\:\boldsymbol{\mathsf{L}}$![]() and $\det \boldsymbol{\mathsf{L}}$
and $\det \boldsymbol{\mathsf{L}}$![]() . As discussed above, these functions are free of poles, but are multivalued. Deforming the integration contour ${C_\rho }$
. As discussed above, these functions are free of poles, but are multivalued. Deforming the integration contour ${C_\rho }$![]() around their branch cuts (see figure 7) gives a non-trivial contribution to (6.1). Letting $\boldsymbol {B}_s(t)$
around their branch cuts (see figure 7) gives a non-trivial contribution to (6.1). Letting $\boldsymbol {B}_s(t)$![]() be the contribution from the integral around the branch cut due to a given species $s$
be the contribution from the integral around the branch cut due to a given species $s$![]() , we can finally write the full solution for $\boldsymbol {\chi }_{\boldsymbol {k}}(t)$
, we can finally write the full solution for $\boldsymbol {\chi }_{\boldsymbol {k}}(t)$![]() as
as
In appendix D, we show that, in the long-time limit $t \to \infty$![]() , the branch-cut contribution $\boldsymbol {B}_s$
, the branch-cut contribution $\boldsymbol {B}_s$![]() for each species is dominated by that arising from the branch point itself, and exhibits an algebraic decay $\propto t^{-3/2}$
for each species is dominated by that arising from the branch point itself, and exhibits an algebraic decay $\propto t^{-3/2}$![]() . The same algebraic decay was found by Kim et al. (Reference Kim, Kishimoto, Horton and Tajima1994) and Kuroda et al. (Reference Kuroda, Sugama, Kanno, Okamoto and Horton1998) in their treatment of the toroidal ITG mode. Such a ‘continuum mode’ (Kuroda et al. Reference Kuroda, Sugama, Kanno, Okamoto and Horton1998; Sugama Reference Sugama1999) is a direct consequence of the multivaluedness of (2.55) and (2.56), in that such multivaluedness gives rise to a branch point and to the resulting discontinuity. This behaviour is qualitatively different from that of a plasma in a straight magnetic field, whose dispersion function is single-valued, meaning that there are no branch cuts and hence no continuum modes. Note that non-exponentially decaying solutions to similar initial-value problems can also be found in other contexts; see, e.g. Taylor (Reference Taylor1965) and Sedlàček (Reference Sedlàček1995).
. The same algebraic decay was found by Kim et al. (Reference Kim, Kishimoto, Horton and Tajima1994) and Kuroda et al. (Reference Kuroda, Sugama, Kanno, Okamoto and Horton1998) in their treatment of the toroidal ITG mode. Such a ‘continuum mode’ (Kuroda et al. Reference Kuroda, Sugama, Kanno, Okamoto and Horton1998; Sugama Reference Sugama1999) is a direct consequence of the multivaluedness of (2.55) and (2.56), in that such multivaluedness gives rise to a branch point and to the resulting discontinuity. This behaviour is qualitatively different from that of a plasma in a straight magnetic field, whose dispersion function is single-valued, meaning that there are no branch cuts and hence no continuum modes. Note that non-exponentially decaying solutions to similar initial-value problems can also be found in other contexts; see, e.g. Taylor (Reference Taylor1965) and Sedlàček (Reference Sedlàček1995).
Equation (6.7) is our final expression for the time evolution of $\boldsymbol {\chi }_{\boldsymbol {k}}(t)$![]() . Depending on whether there are any unstable solutions, we find that either: (i) there are solutions to $\mathcal {D}(p) = 0$
. Depending on whether there are any unstable solutions, we find that either: (i) there are solutions to $\mathcal {D}(p) = 0$![]() for $\mathrm {Re}(p) > 0$
for $\mathrm {Re}(p) > 0$![]() , in which case, the long-time solution is dominated by the solution with largest $\mathrm {Re}(p)$
, in which case, the long-time solution is dominated by the solution with largest $\mathrm {Re}(p)$![]() ; or (ii) there are no solutions to $\mathcal {D}(p) = 0$
; or (ii) there are no solutions to $\mathcal {D}(p) = 0$![]() for $\mathrm {Re}(p) > 0$
for $\mathrm {Re}(p) > 0$![]() , in which case, the long-time solution is dominated by the ballistic response (6.4) and by waves with frequencies $\omega = {\rm i}p_s = -k_\parallel ^2v_{{\rm th}s}^2/8\omega _{ds}$
, in which case, the long-time solution is dominated by the ballistic response (6.4) and by waves with frequencies $\omega = {\rm i}p_s = -k_\parallel ^2v_{{\rm th}s}^2/8\omega _{ds}$![]() that exhibit a non-exponential decay $\propto t^{-3/2}$
that exhibit a non-exponential decay $\propto t^{-3/2}$![]() .
.
7 From drift kinetics to gyrokinetics
The analytical forms of the integrals derived in § 4 are not without their limitations: in their derivation, we assumed both the drift-kinetic limit and the case of equal magnetic drifts (see § 2.3). We will now devote some space to a brief discussion of how one can relax these assumptions.
7.1 Bessel functions
The drift-kinetic assumption is perhaps the more egregious approximation, especially given that the presence of finite-Larmor-radius effects can have a non-trivial impact on the plasma dynamics (see, e.g. Smolyakov et al. Reference Smolyakov, Yagi and Kishimoto2002; Parisi et al. Reference Parisi, Parra, Roach, Giroud, Dorland, Hatch, Barnes, Hillesheim, Aiba and Ball2020, Reference Parisi, Parra, Roach, Hardman, Schekochihin, Abel, Aiba, Ball, Barnes and Chapman-Oplopoiou2022, and references therein). Thankfully, however, it can be relaxed if one is willing to pay the price of complicated analytical expressions. Noting that $2 {\rm J}_0(b_s) {\rm J}_1(b_s) = - \partial {\rm J}_0^2(b_s)/\partial b_s$![]() , it is clear that the Bessel functions ${\rm J}_0$
, it is clear that the Bessel functions ${\rm J}_0$![]() and ${\rm J}_1$
and ${\rm J}_1$![]() always appear quadratically in (2.39)–(2.43), for which there are known, rapidly converging Taylor series (Neumann Reference Neumann1871; Watson Reference Watson1966):
always appear quadratically in (2.39)–(2.43), for which there are known, rapidly converging Taylor series (Neumann Reference Neumann1871; Watson Reference Watson1966):

Using this expansion in (2.39)–(2.43), one can, in principle, compute each of the resulting integrals analytically and thus obtain an absolutely convergent series for the resulting gyrokinetic dispersion relation. This is done by noticing that their argument $b_s$![]() only appears quadratically as $b_s^2 = \mu k_\perp ^2 \rho _s^2$
only appears quadratically as $b_s^2 = \mu k_\perp ^2 \rho _s^2$![]() and thus the additional factors of $\mu$
and thus the additional factors of $\mu$![]() can be handled by partial differentiation with respect to $b$
can be handled by partial differentiation with respect to $b$![]() before setting $a = b$
before setting $a = b$![]() in (2.39)–(2.43). For example, (2.39) would give
in (2.39)–(2.43). For example, (2.39) would give

with the other required integrals, viz. $\mathcal {J}^{(s)}_{a,b}$![]() and $\partial _a \mathcal {I}^{(s)}_{a,b}$
and $\partial _a \mathcal {I}^{(s)}_{a,b}$![]() , satisfying similar expressions. We remind the reader that $\mathcal {I}_{a,b}^{(s)}$
, satisfying similar expressions. We remind the reader that $\mathcal {I}_{a,b}^{(s)}$![]() refers to the FLR-containing integral (2.39), while ${\rm I}_{a,b}$
refers to the FLR-containing integral (2.39), while ${\rm I}_{a,b}$![]() is the integral (2.55) on which we have focused throughout most of this paper. Doing this calculation by hand seems rather daunting given the complicated expressions even for the low-order derivatives $\partial _b^2 {\rm I}_{a,b}$
is the integral (2.55) on which we have focused throughout most of this paper. Doing this calculation by hand seems rather daunting given the complicated expressions even for the low-order derivatives $\partial _b^2 {\rm I}_{a,b}$![]() and $\partial _b {\rm J}_{a,b}$
and $\partial _b {\rm J}_{a,b}$![]() [see (B14) and (B15), respectively]. In practice, however, only a few terms would be needed due to the rapid convergence of the Taylor series (7.1). Those wishing to compute these terms to an arbitrary order may want to do so by using symbolic libraries (e.g. those in Wolfram Mathematica) to calculate the derivatives analytically, which can then be imported into an associated numerical solver. An alternative approach would be to implement a recursive scheme to calculate numerically the $m$
[see (B14) and (B15), respectively]. In practice, however, only a few terms would be needed due to the rapid convergence of the Taylor series (7.1). Those wishing to compute these terms to an arbitrary order may want to do so by using symbolic libraries (e.g. those in Wolfram Mathematica) to calculate the derivatives analytically, which can then be imported into an associated numerical solver. An alternative approach would be to implement a recursive scheme to calculate numerically the $m$![]() th-order derivatives from the $(m-1)$
th-order derivatives from the $(m-1)$![]() th ones.
th ones.
7.2 General magnetic drifts
Our second approximation was to neglect the difference between the curvature and ${\boldsymbol {\nabla }} \! B$![]() drifts, taking their associated drift frequencies to be equal, i.e. $\zeta _{\kappa s} = \zeta _{{\boldsymbol {\nabla }} \! B s}$
drifts, taking their associated drift frequencies to be equal, i.e. $\zeta _{\kappa s} = \zeta _{{\boldsymbol {\nabla }} \! B s}$![]() , as in (2.54). While this approximation is relatively well satisfied in the context of magnetic-confinement fusion, there are certainly other systems in which it is not, e.g. space and astrophysical plasmas. By a simple change of variables to $\mu ' = \zeta _{Bs}\mu /\zeta _{\kappa s}$
, as in (2.54). While this approximation is relatively well satisfied in the context of magnetic-confinement fusion, there are certainly other systems in which it is not, e.g. space and astrophysical plasmas. By a simple change of variables to $\mu ' = \zeta _{Bs}\mu /\zeta _{\kappa s}$![]() in (2.52), we find
in (2.52), we find

Therefore, the integral (2.52) that enters (2.30)–(2.38) at $a=b$![]() can be found in terms of the known integrals (2.55) via
can be found in terms of the known integrals (2.55) via
where now $b = a \zeta _{\kappa s}/\zeta _{Bs}$![]() . Finally, to find ${\rm I}_{a,b}$
. Finally, to find ${\rm I}_{a,b}$![]() for $a\neq b$
for $a\neq b$![]() , one can Taylor expand
, one can Taylor expand

Fortunately, just as in § 7.1, one can find closed, albeit complicated, analytical expressions for $\partial _b^m {\rm I}_{a,b}|_{a=b}$![]() for any $m$
for any $m$![]() . The expansion should converge for arbitrary positive $a$
. The expansion should converge for arbitrary positive $a$![]() and $b$
and $b$![]() since (7.5) is equivalent to expanding ${\rm e}^{-(b-a)\mu }$
since (7.5) is equivalent to expanding ${\rm e}^{-(b-a)\mu }$![]() in (4.10) using its absolutely convergent Taylor series.
in (4.10) using its absolutely convergent Taylor series.
8 Electrostatic ITG: a detailed example
To illustrate the results of § 4, we provide an explicit calculation of the dispersion relation in the simple case of an electrostatic, ion-scale, temperature-gradient-driven instability, and compare the solution with well-known kinetic and fluid limits.
In particular, we consider a two-species plasma of ions and electrons of comparable temperatures, $T_{0i}\sim T_{0e}$![]() . Since we want to consider electrostatic physics, we assume
. Since we want to consider electrostatic physics, we assume
where $d_s = \sqrt {m_sc^2 / 4{\rm \pi} n_{0s} q_s^2}$![]() is the skin depth of species s. Therefore, to lowest order, $A_{\parallel \boldsymbol {k}}$
is the skin depth of species s. Therefore, to lowest order, $A_{\parallel \boldsymbol {k}}$![]() and ${\delta \! B}_{\parallel \boldsymbol {k}}$
and ${\delta \! B}_{\parallel \boldsymbol {k}}$![]() do not contribute to (2.17), and (2.29) simplifies to
do not contribute to (2.17), and (2.29) simplifies to
This implies that the dispersion relation is given simply by $\text {L}_{\phi \phi } = 0$![]() . Furthermore, we consider the frequencies of the perturbations to be comparable to the parallel streaming and drift frequencies of the ions, as well as the magnetic-drift frequency, viz.
. Furthermore, we consider the frequencies of the perturbations to be comparable to the parallel streaming and drift frequencies of the ions, as well as the magnetic-drift frequency, viz.
The relevant equilibrium length scales in our problem are thus the ion-density and ion-temperature gradients $L_{n_i}^{-1}$![]() and $L_{T_i}^{-1}$
and $L_{T_i}^{-1}$![]() , respectively [see (2.6)], and the gradient of the magnetic field $L_B^{-1} \equiv -\partial \ln B_0 / \partial x$
, respectively [see (2.6)], and the gradient of the magnetic field $L_B^{-1} \equiv -\partial \ln B_0 / \partial x$![]() . In the small-mass-ratio limit, $m_e/m_i \ll 1$
. In the small-mass-ratio limit, $m_e/m_i \ll 1$![]() , (8.3) implies
, (8.3) implies
i.e. the electrons stream quickly along the fields lines. Thus, $\zeta _e \sim \zeta _{*e} \ll \zeta _i \sim \zeta _{*i}$![]() , and the electron contributions to $\text {L}_{\phi \phi }$
, and the electron contributions to $\text {L}_{\phi \phi }$![]() can be ignored. Choosing $q_r = q_i = Ze$
can be ignored. Choosing $q_r = q_i = Ze$![]() , $T_{0r} = T_{0i}$
, $T_{0r} = T_{0i}$![]() , and ${n_{0r} = n_{0i}}$
, and ${n_{0r} = n_{0i}}$![]() , the expression (2.30) simplifies to
, the expression (2.30) simplifies to
where $\tau \equiv T_{0i}/ZT_{0e}$![]() is the temperature ratio. To avoid carrying around an extra minus sign, we shall define $D \equiv -\text {L}_{\phi \phi }$
is the temperature ratio. To avoid carrying around an extra minus sign, we shall define $D \equiv -\text {L}_{\phi \phi }$![]() , the object in whose zeros we shall be interested. Using (4.14), we obtain the principal branch of the ITG dispersion relation:
, the object in whose zeros we shall be interested. Using (4.14), we obtain the principal branch of the ITG dispersion relation:
where we have dropped the $i$![]() subscripts, $\zeta _\pm$
subscripts, $\zeta _\pm$![]() are given by (4.12) and we are using the shorthand notation $Z_\pm \equiv Z(\zeta _\pm )$
are given by (4.12) and we are using the shorthand notation $Z_\pm \equiv Z(\zeta _\pm )$![]() . Note that the principal branch (i.e. $\lambda =+$
. Note that the principal branch (i.e. $\lambda =+$![]() ) is implicitly used everywhere, but we have dropped the associated superscripts to reduce the notational clutter.
) is implicitly used everywhere, but we have dropped the associated superscripts to reduce the notational clutter.
We can use (5.2) and (5.6) to verify that (8.6) converges to the correct limits in the case of: vanishingly small magnetic gradients (i.e. $\zeta _d \to 0$![]() )
)
and of 2-D perturbations (i.e. $\zeta \sim \zeta _*\sim \zeta _d\to \infty$![]() )
)
where $\varOmega = \zeta /2\zeta _d = ip/2\omega _d$![]() and $\varOmega _* = \zeta _* / 2\zeta _d = \omega _*/2\omega _d$
and $\varOmega _* = \zeta _* / 2\zeta _d = \omega _*/2\omega _d$![]() . Note that (8.8) agrees with the expressions obtained by Biglari et al. (Reference Biglari, Diamond and Rosenbluth1989) and Zocco et al. (Reference Zocco, Xanthopoulos, Doerk, Connor and Helander2018) in a similar limit to (8.3).
. Note that (8.8) agrees with the expressions obtained by Biglari et al. (Reference Biglari, Diamond and Rosenbluth1989) and Zocco et al. (Reference Zocco, Xanthopoulos, Doerk, Connor and Helander2018) in a similar limit to (8.3).
In figure 8, we compare the solutions to (8.6) and (8.7) for the case of zero density gradient, viz. $\omega _{*} = 0$![]() , but non-zero temperature gradient, so $\eta \omega _{*} \propto L_{T_{i}}^{-1} \neq ~0$
, but non-zero temperature gradient, so $\eta \omega _{*} \propto L_{T_{i}}^{-1} \neq ~0$![]() . The growth rates agree well only at simultaneously large perpendicular and small parallel wavelengths; this is to be expected given that the slab dispersion relation (8.7) does not capture the effect of magnetic drifts, which are most important at large parallel wavelengths. There is poorer agreement between the frequencies of the two dispersion relations.
. The growth rates agree well only at simultaneously large perpendicular and small parallel wavelengths; this is to be expected given that the slab dispersion relation (8.7) does not capture the effect of magnetic drifts, which are most important at large parallel wavelengths. There is poorer agreement between the frequencies of the two dispersion relations.

Figure 8. A comparison between the growth rate and frequency of the most unstable solution to the kinetic dispersion relation with magnetic effects (8.6) and the slab dispersion relation (8.7), represented by the solid and dotted lines, respectively. Here, $\rho _s = \rho _i / \sqrt {2\tau }$![]() is the ion sound radius, and we have set $\tau =0.1$
is the ion sound radius, and we have set $\tau =0.1$![]() and $\tau L_B / 2L_{T_{i}} = 2$
and $\tau L_B / 2L_{T_{i}} = 2$![]() .
.
We can also compare the solutions to (8.6) with those obtained from a simple three-field fluid model of the ITG instability in a slab with magnetic curvature. The model consists of the following equations:
where $\varphi \equiv Ze\phi /T_{0i}$![]() , $u_\parallel$
, $u_\parallel$![]() , and $\delta T_i/T_{0i}$
, and $\delta T_i/T_{0i}$![]() are the perturbed electrostatic potential, ion parallel flow, and ion temperature, respectively. These equations can be derived by substituting a perturbed Maxwellian for $h_i$
are the perturbed electrostatic potential, ion parallel flow, and ion temperature, respectively. These equations can be derived by substituting a perturbed Maxwellian for $h_i$![]() in the ion gyrokinetic equation and taking the three relevant velocity moments (cf. Newton, Cowley & Loureiro Reference Newton, Cowley and Loureiro2010 or the cold-ion fluid model of Ivanov et al. Reference Ivanov, Schekochihin and Dorland2022 but with additional $\tau \sim 1$
in the ion gyrokinetic equation and taking the three relevant velocity moments (cf. Newton, Cowley & Loureiro Reference Newton, Cowley and Loureiro2010 or the cold-ion fluid model of Ivanov et al. Reference Ivanov, Schekochihin and Dorland2022 but with additional $\tau \sim 1$![]() terms). Figure 9 shows a comparison between the kinetic and fluid growth rates at a fixed value of $\tau$
terms). Figure 9 shows a comparison between the kinetic and fluid growth rates at a fixed value of $\tau$![]() and varying $k_\parallel L_B$
and varying $k_\parallel L_B$![]() . We see that the fluid approximation is decent for small $k_\parallel L_B$
. We see that the fluid approximation is decent for small $k_\parallel L_B$![]() , but fails for larger ones because of its lack of kinetic effects. Making the ions cold, i.e. lowering $\tau$
, but fails for larger ones because of its lack of kinetic effects. Making the ions cold, i.e. lowering $\tau$![]() , improves the accuracy of the fluid approximation, as in figure 10.
, improves the accuracy of the fluid approximation, as in figure 10.
9 Summary and discussion
We have considered the problem of local linear gyrokinetics in a curved magnetic field, expressing the associated dispersion relation in terms of velocity-space integrals featuring resonances arising both from parallel streaming and from magnetic drifts (§ 2). Previously, exact solutions for these integrals were known either in the absence of magnetic drifts – leading to the well-known plasma dispersion function $Z (\zeta )$![]() – or in the 2-D limit (§ 3). In the case of drift kinetics (i.e. no finite-Larmor-radius effects) and equal magnetic drifts, we showed that these resonances can in fact be handled simultaneously without any additional approximations or expansions, and that the integrals can be expressed exactly in terms of a generalised plasma dispersion function consisting of products of $Z$
– or in the 2-D limit (§ 3). In the case of drift kinetics (i.e. no finite-Larmor-radius effects) and equal magnetic drifts, we showed that these resonances can in fact be handled simultaneously without any additional approximations or expansions, and that the integrals can be expressed exactly in terms of a generalised plasma dispersion function consisting of products of $Z$![]() functions and their derivatives (§ 4). Since there exist known algorithms for the computation of the $Z$
functions and their derivatives (§ 4). Since there exist known algorithms for the computation of the $Z$![]() function, the resulting expressions are efficient to evaluate numerically and can easily be handled analytically through known asymptotic expansions. Solutions to the exact dispersion relation for the electrostatic ITG instability, derived using this method, were then compared with approximate solutions in the previously known limits, showing poor agreement for the majority of parameters and wavenumbers considered (§ 8). This demonstrates that to properly capture the growth rate and frequency of kinetic instabilities in the presence of a curved magnetic field, one must simultaneously resolve the resonances associated with parallel streaming and magnetic drifts, for which this paper provides the first known exact analytical solution.
function, the resulting expressions are efficient to evaluate numerically and can easily be handled analytically through known asymptotic expansions. Solutions to the exact dispersion relation for the electrostatic ITG instability, derived using this method, were then compared with approximate solutions in the previously known limits, showing poor agreement for the majority of parameters and wavenumbers considered (§ 8). This demonstrates that to properly capture the growth rate and frequency of kinetic instabilities in the presence of a curved magnetic field, one must simultaneously resolve the resonances associated with parallel streaming and magnetic drifts, for which this paper provides the first known exact analytical solution.
In § 7, we discussed how the assumptions of no finite-Larmor-radius effects and equal magnetic drifts can be relaxed using absolutely convergent Taylor-series expansions, and thus solve the more general linear gyrokinetic system. This results in expressions that naturally capture the multivaluedness of the underlying dispersion relation and handle the integration of resonant denominators exactly.
An immediate practical application of this work would be to use the derived analytical expressions to implement an efficient and accurate solver for drift-kinetic/gyrokinetic instabilities in the local limit considered in this paper. Such a solver could be used to benchmark both reduced models and gyrokinetic solvers. It could also be exploited to explore the equilibrium parameter space in search of new instabilities or to investigate the properties of subdominant ones, i.e. those whose growth rate is smaller than the largest growth rate in the system; this is typically difficult to do in most gyrokinetic solvers. Such subdominant instabilities have been proposed as one of the possible explanations for the lack of saturation observed in certain electromagnetic gyrokinetic simulations. With this in mind, we consider the implementation of such a gyrokinetic dispersion-relation solver to be a natural extension of this work that will produce a useful practical tool in the study of gyrokinetic instabilities and turbulence.
Acknowledgements
Editor P. Helander thanks the referees for their advice in evaluating this article.
Funding
This work has been carried out within the framework of the EUROfusion Consortium and has received funding from the Euratom research and training programme 2014–2018 and 2019–2020 under Grant Agreement No. 633053, and from the UKRI Energy Programme (EP/T012250/1). The views and opinions expressed herein do not necessarily reflect those of the European Commission. This work was supported by the Engineering and Physical Sciences Research Council (EPSRC) [EP/R034737/1]. T.A. was supported by a UK EPSRC studentship.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Calculation of ${\rm J}_{a,b}$
In this appendix, we derive the expression (4.15) for ${\rm J}_{a,b}$![]() . The calculation proceeds in a similar way to that of ${\rm I}_{a,b}$
. The calculation proceeds in a similar way to that of ${\rm I}_{a,b}$![]() in § 4.2. Starting from (2.56), we consider the integral over $u$
in § 4.2. Starting from (2.56), we consider the integral over $u$![]() separately and so write
separately and so write
Defining $u_\pm$![]() as in (4.3) and making the same choice for the branch cut and square-root branch, a partial-fractions expansion of the integrand yields
as in (4.3) and making the same choice for the branch cut and square-root branch, a partial-fractions expansion of the integrand yields

As previously, the sign of the imaginary part of $u_\pm$![]() is always positive. Therefore, the first integral in the brackets in (A2) is manifestly the plasma dispersion function, while the second can be turned into a plasma dispersion function under the change of variables $u \mapsto -u$
is always positive. Therefore, the first integral in the brackets in (A2) is manifestly the plasma dispersion function, while the second can be turned into a plasma dispersion function under the change of variables $u \mapsto -u$![]() . Thus, it follows that (A2) can be written as
. Thus, it follows that (A2) can be written as
Using the property (confirmed by direct calculation)
we can write $\tilde {{\rm J}}_a^+$![]() as
as
Alternatively, using
we can also write
Therefore, by substitution into the first expression in (A1), we find

where, in going from the first line to the second, we have integrated by parts in the first integral and have used (A5). Equation (A8) can be straightforwardly rearranged to yield (4.15).
Appendix B. Calculation of derivatives of ${\rm I}_{a,b}$
Even though we are unable to evaluate (4.7) exactly in the case where $a$![]() and $b$
and $b$![]() are distinct, we are still able to find its derivatives with respect to $a$
are distinct, we are still able to find its derivatives with respect to $a$![]() and $b$
and $b$![]() at $a=b=1$
at $a=b=1$![]() , a task to which this appendix is devoted.
, a task to which this appendix is devoted.
B.1 Derivatives for general $a$ and $b$
and $b$
To avoid clutter, we shall suppress the $\lambda =+$![]() indices until appendix B.2. For this subsection, assume that all expressions ${\rm I}_{a,b}$
indices until appendix B.2. For this subsection, assume that all expressions ${\rm I}_{a,b}$![]() , ${\rm J}_{a,b}$
, ${\rm J}_{a,b}$![]() , $Q_{a,b}$
, $Q_{a,b}$![]() , and $\zeta _\pm$
, and $\zeta _\pm$![]() come with a $\lambda =+$
come with a $\lambda =+$![]() .
.
Using (4.3), we can show that
and so the derivative of (4.7) with respect to $a$![]() becomes
becomes

where we have defined the integral
In going from the first line of (B2) to the second, we made use of the fact, obvious from the definition (4.3), that
while going from the second to the third, we have recognised the first expression in the curly brackets as (A5) and integrated by parts the second.
Similarly, taking a derivative of (4.7) with respect to $b$![]() , and making use of (4.8) and (4.12), we have that
, and making use of (4.8) and (4.12), we have that
Since

(B5) becomes
where we have made use of (A5) again. It is clear from (B2) and (B7) that we need to find $Q_{a,b}$![]() to obtain expressions for $\partial _a {\rm I}_{a,b}$
to obtain expressions for $\partial _a {\rm I}_{a,b}$![]() and $\partial _b {\rm I}_{a,b}$
and $\partial _b {\rm I}_{a,b}$![]() . Though it is possible to do so via direct manipulation of the integrand of (B3), we prefer an alternative approach. Using
. Though it is possible to do so via direct manipulation of the integrand of (B3), we prefer an alternative approach. Using
in (2.56) gives
Substituting (B2) and (B7) into (B9), and rearranging, we obtain the following expression for $Q_{a,b}$![]() in terms of ${\rm I}_{a,b}$
in terms of ${\rm I}_{a,b}$![]() and ${\rm J}_{a,b}$
and ${\rm J}_{a,b}$![]() :
:
In a similar way, taking a $\partial _b$![]() derivative of (4.15), we find
derivative of (4.15), we find
B.2 Derivatives at $a=b$
Finally, using (4.15), (B2), (B7) and (B10), setting $a=b$![]() and simultaneously expressing both branches using (4.13), we obtain
and simultaneously expressing both branches using (4.13), we obtain


Appendix C. Properties of the branches of the dispersion function
The main convenience of choosing the branch cut along the negative real line in § 4.1 is the relationship $\sqrt [+]{z^*} = \sqrt [+]{z}^*$![]() for any $z \in \mathbb {C}$
for any $z \in \mathbb {C}$![]() . It is then easy to see that the expressions (4.13) satisfy
. It is then easy to see that the expressions (4.13) satisfy
and that (4.13) implies
Additionally, it is straightforward to show that the $Z$![]() function satisfies
function satisfies
Then, using (4.14) and (C1)–(C4), we have

and

Similarly, using (4.16), we find
The derivatives of ${\rm I}_{a,b}$![]() , given by (B12)–(B14), and $\partial _b{\rm J}_{a,b}\vert _{a=b}$
, given by (B12)–(B14), and $\partial _b{\rm J}_{a,b}\vert _{a=b}$![]() , given by (B15), can also be shown to have the properties (C5)–(C6) and (C7)–(C8), respectively.
, given by (B15), can also be shown to have the properties (C5)–(C6) and (C7)–(C8), respectively.
Recall that the frequencies, which enter the dispersion matrix elements (2.30)–(2.38), are functions of $\zeta _s \propto p$![]() , $\zeta _{*s} \propto k_y$
, $\zeta _{*s} \propto k_y$![]() , and $\zeta _{ds} \propto k_y$
, and $\zeta _{ds} \propto k_y$![]() [see (2.13), (2.15), (2.27) and (2.54)]. It is then evident that $p \mapsto p^*$
[see (2.13), (2.15), (2.27) and (2.54)]. It is then evident that $p \mapsto p^*$![]() maps $\zeta _s \mapsto -\zeta _s^*$
maps $\zeta _s \mapsto -\zeta _s^*$![]() , $p \mapsto -p^*$
, $p \mapsto -p^*$![]() maps $\zeta _s \mapsto \zeta _s^*$
maps $\zeta _s \mapsto \zeta _s^*$![]() , and the inversion $\boldsymbol {k} \mapsto -\boldsymbol {k}$
, and the inversion $\boldsymbol {k} \mapsto -\boldsymbol {k}$![]() results in $\zeta _{*s} \mapsto -\zeta _{*s}$
results in $\zeta _{*s} \mapsto -\zeta _{*s}$![]() and $\zeta _{ds} \mapsto -\zeta _{ds}$
and $\zeta _{ds} \mapsto -\zeta _{ds}$![]() (recall that the sign of the parallel wavenumber $k_\parallel$
(recall that the sign of the parallel wavenumber $k_\parallel$![]() does not enter the normalised frequencies, as we noted in footnote 1). Combining this with (C5)–(C8), it is then straightforward to show that the dispersion matrix $\boldsymbol{\mathsf{L}}$
does not enter the normalised frequencies, as we noted in footnote 1). Combining this with (C5)–(C8), it is then straightforward to show that the dispersion matrix $\boldsymbol{\mathsf{L}}$![]() and its elements (2.30)–(2.38) satisfy
and its elements (2.30)–(2.38) satisfy

and
where the vector $\boldsymbol {\lambda } = (\lambda _1, \lambda _2,\ldots, \lambda _N)$![]() labels the branches the double-valued functions that constitute $\boldsymbol{\mathsf{L}}$
labels the branches the double-valued functions that constitute $\boldsymbol{\mathsf{L}}$![]() for each of the $N$
for each of the $N$![]() particle species. Therefore, for the dispersion function $D=\det \boldsymbol{\mathsf{L}}$
particle species. Therefore, for the dispersion function $D=\det \boldsymbol{\mathsf{L}}$![]() , we have, from (C9),
, we have, from (C9),
and, from (C10),
Figures 11 and 12 show an example of the four branches of the dispersion function in the case of a two-species plasma. In particular, the property (C12) is illustrated clearly in figure 11.

Figure 11. A plot in the complex plane of the dispersion function $D(p)={\mathsf{L}}_{\phi \phi }$![]() for an electrostatic, two-species plasma composed of ion and electrons, for the following parameters: $m_i / m_e = 2$
for an electrostatic, two-species plasma composed of ion and electrons, for the following parameters: $m_i / m_e = 2$![]() , $q_i = -q_e=e$
, $q_i = -q_e=e$![]() , $T_{0i} = T_{0e}$
, $T_{0i} = T_{0e}$![]() , $k_y \rho _i = 1$
, $k_y \rho _i = 1$![]() , $k_\parallel L_B = 1$
, $k_\parallel L_B = 1$![]() , and $L_{T_i} = L_B$
, and $L_{T_i} = L_B$![]() . The panels show the four branches of $D$
. The panels show the four branches of $D$![]() , labelled by $\boldsymbol {\lambda } = (\lambda _i, \lambda _e)$
, labelled by $\boldsymbol {\lambda } = (\lambda _i, \lambda _e)$![]() as shown (see § 4.4). Here, we are using the principal branch cut for the square root. The colour brightness shows the magnitude $|D|$
as shown (see § 4.4). Here, we are using the principal branch cut for the square root. The colour brightness shows the magnitude $|D|$![]() , while its hue shows the phase $\arg D$
, while its hue shows the phase $\arg D$![]() . The relation (C12), $D^{\boldsymbol {\lambda }}(-p^*, \boldsymbol {k}) = D^{-\boldsymbol {\lambda }}(p, \boldsymbol {k})^*$
. The relation (C12), $D^{\boldsymbol {\lambda }}(-p^*, \boldsymbol {k}) = D^{-\boldsymbol {\lambda }}(p, \boldsymbol {k})^*$![]() , is evident in the pairs (a)–(d) and (b)–(c): flipping the sign of $\boldsymbol {\lambda }$
, is evident in the pairs (a)–(d) and (b)–(c): flipping the sign of $\boldsymbol {\lambda }$![]() corresponds to mirroring the real part of $p$
corresponds to mirroring the real part of $p$![]() and taking the complex conjugate of $D$
and taking the complex conjugate of $D$![]() (note the change in colour). Furthermore, crossing the electron branch cut flips the sign of $\lambda _e$
(note the change in colour). Furthermore, crossing the electron branch cut flips the sign of $\lambda _e$![]() and so corresponds to jumping horizontally between the panels; crossing the ion branch cut corresponds to jumping vertically between them.
and so corresponds to jumping horizontally between the panels; crossing the ion branch cut corresponds to jumping vertically between them.

Figure 12. The same as figure 11 but with the branch cuts rotated to point towards $\text {Re}(p) \to -\infty$![]() . As previously, crossing the electron branch cut flips the sign of $\lambda _e$
. As previously, crossing the electron branch cut flips the sign of $\lambda _e$![]() and so corresponds to jumping horizontally between the panels, while crossing the ion branch cut corresponds to jumping vertically between the panels. For practical purposes, we are only interested in the ‘dispersion’ branch $\mathcal {D}$
and so corresponds to jumping horizontally between the panels, while crossing the ion branch cut corresponds to jumping vertically between the panels. For practical purposes, we are only interested in the ‘dispersion’ branch $\mathcal {D}$![]() (see discussion in § 6) shown in panel (a) as it is that one that enters the inverse Laplace transform.
(see discussion in § 6) shown in panel (a) as it is that one that enters the inverse Laplace transform.
Appendix D. Integral around the branch cut
This appendix is devoted to calculating the asymptotic contribution to (6.1) in the limit $t\to \infty$![]() arising from the integral around one of the branch cuts of $\hat {\boldsymbol {\chi }}_{\boldsymbol {k}}(p)$
arising from the integral around one of the branch cuts of $\hat {\boldsymbol {\chi }}_{\boldsymbol {k}}(p)$![]() . Similar calculations already exist in the literature (e.g. Kim et al. Reference Kim, Kishimoto, Horton and Tajima1994; Kuroda et al. Reference Kuroda, Sugama, Kanno, Okamoto and Horton1998); we are including one here for completeness.
. Similar calculations already exist in the literature (e.g. Kim et al. Reference Kim, Kishimoto, Horton and Tajima1994; Kuroda et al. Reference Kuroda, Sugama, Kanno, Okamoto and Horton1998); we are including one here for completeness.
Recall that there is one branch cut for each particle species, associated with the branch point $p_s$![]() (6.3). We choose the branch cut to be parallel to the real $p$
(6.3). We choose the branch cut to be parallel to the real $p$![]() axis and denote the contour around this branch cut $C_\text {br}$
axis and denote the contour around this branch cut $C_\text {br}$![]() , as in figure 13. Here, $C_\text {br}$
, as in figure 13. Here, $C_\text {br}$![]() consists of a semi-circular arc $C_\varepsilon$
consists of a semi-circular arc $C_\varepsilon$![]() of radius $\varepsilon$
of radius $\varepsilon$![]() around the branch point, where we choose $\varepsilon \sim t^{-2}$
around the branch point, where we choose $\varepsilon \sim t^{-2}$![]() and two horizontal, semi-infinite segments $C_\pm$
and two horizontal, semi-infinite segments $C_\pm$![]() along $\mathrm {Im}(p) = \mathrm {Im}(p_s) \pm \varepsilon$
along $\mathrm {Im}(p) = \mathrm {Im}(p_s) \pm \varepsilon$![]() , viz.
, viz.
Let us calculate each of the contributions to (D1) in turn.

Figure 13. The contour of integration $C_\text {br}$![]() around the branch cut – chosen to be parallel to the real $p$
around the branch cut – chosen to be parallel to the real $p$![]() axis – with the latter indicated by the zigzag line. The $C_\pm$
axis – with the latter indicated by the zigzag line. The $C_\pm$![]() are the horizontal, semi-infinite segments along $\mathrm {Im}(p) = \mathrm {Im}(p_s) \pm \varepsilon$
are the horizontal, semi-infinite segments along $\mathrm {Im}(p) = \mathrm {Im}(p_s) \pm \varepsilon$![]() that connect the vertical contour at $\mathrm {Re}(p) \to -\infty$
that connect the vertical contour at $\mathrm {Re}(p) \to -\infty$![]() (see figure 7) to the semi-circular arc $C_\varepsilon$
(see figure 7) to the semi-circular arc $C_\varepsilon$![]() around the branch point.
around the branch point.
For $C_\varepsilon$![]() , we change variables to $p = p_s + \varepsilon {\rm e}^{{\rm i} \theta }$
, we change variables to $p = p_s + \varepsilon {\rm e}^{{\rm i} \theta }$![]() for $\theta \in [-{\rm \pi} /2, {\rm \pi}/2]$
for $\theta \in [-{\rm \pi} /2, {\rm \pi}/2]$![]() . It straightforwardly follows that, since $\varepsilon \sim t^{-2}$
. It straightforwardly follows that, since $\varepsilon \sim t^{-2}$![]() ,
,

Turning our attention to $C_\pm$![]() , we set $p = p_s + \xi \pm {\rm i}\varepsilon$
, we set $p = p_s + \xi \pm {\rm i}\varepsilon$![]() and find
and find

where we have split the integration interval using some positive real $\delta \ll 1$![]() . The first integral in the square brackets of (D3) is bounded by an exponential, viz.
. The first integral in the square brackets of (D3) is bounded by an exponential, viz.

and so it is exponentially small in the limit of $t \rightarrow \infty$![]() . For the second integral, we know that $|\xi |\leqslant \delta \ll 1$
. For the second integral, we know that $|\xi |\leqslant \delta \ll 1$![]() , and so it is natural to Taylor-expand the integrand. Note that the function $\hat {\boldsymbol {\chi }}_{\boldsymbol {k}}$
, and so it is natural to Taylor-expand the integrand. Note that the function $\hat {\boldsymbol {\chi }}_{\boldsymbol {k}}$![]() contains both parts that are discontinuous across the branch cut (related to species $s$
contains both parts that are discontinuous across the branch cut (related to species $s$![]() ), as well as some that are continuous (related to species other than $s$
), as well as some that are continuous (related to species other than $s$![]() ). The discontinuity is due to the square-root terms in ${\rm I}_{a,b}$
). The discontinuity is due to the square-root terms in ${\rm I}_{a,b}$![]() and ${\rm J}_{a,b}$
and ${\rm J}_{a,b}$![]() , manifest in the expression for $\zeta _\pm$
, manifest in the expression for $\zeta _\pm$![]() (4.13). These square roots appear only as arguments of analytic functions. Therefore, the discontinuity of $\hat {\boldsymbol {\chi }}_{\boldsymbol {k}}$
(4.13). These square roots appear only as arguments of analytic functions. Therefore, the discontinuity of $\hat {\boldsymbol {\chi }}_{\boldsymbol {k}}$![]() across the branch cut can be made explicit by writing
across the branch cut can be made explicit by writing
where $\hat {\boldsymbol {\chi }}_{\boldsymbol {k}}$![]() is an analytic function of both of its arguments. (The principal branch is the appropriate one for $\sqrt {p-p_s}$
is an analytic function of both of its arguments. (The principal branch is the appropriate one for $\sqrt {p-p_s}$![]() only after performing the rotation of the branch cuts to align them in the horizontal direction in the $p$
only after performing the rotation of the branch cuts to align them in the horizontal direction in the $p$![]() complex plane, see § 6.) Noting that
complex plane, see § 6.) Noting that
for $p = p_s + \xi \pm {\rm i}\varepsilon$![]() , respectively, we find
, respectively, we find
where we have ignored terms $O(\delta )$![]() or $O(\varepsilon )$
or $O(\varepsilon )$![]() in the square brackets and $\partial \hat {\boldsymbol {\chi }}_{\boldsymbol {k}}(p_s) / \partial \sqrt [+]{p-p_s}$
in the square brackets and $\partial \hat {\boldsymbol {\chi }}_{\boldsymbol {k}}(p_s) / \partial \sqrt [+]{p-p_s}$![]() denotes the partial derivative of $\hat {\boldsymbol {\chi }}_{\boldsymbol {k}}$
denotes the partial derivative of $\hat {\boldsymbol {\chi }}_{\boldsymbol {k}}$![]() with respect to its second parameter in (D5) evaluated at $p=p_s$
with respect to its second parameter in (D5) evaluated at $p=p_s$![]() , i.e. at $\xi = 0$
, i.e. at $\xi = 0$![]() . Using (D8), we then find
. Using (D8), we then find

Using
we finally arrive at
which is the required result.