Article contents
Integrodifferential models of electron transport for negative ion sources
Published online by Cambridge University Press: 08 October 2015
Abstract
Thanks to the presence of a transverse magnetic flux density (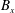 $B_{x}$ and
$B_{x}$ and 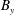 $B_{y}$ where
$B_{y}$ where  $z$ is the extraction axis), the undesired extraction of electrons from a negative ion source is reduced and it is due to collisions. The electron transport is studied with a kinetic model, including Vlasov–Poisson effects and atomic collisions. The integrodifferential equations (IDE) resulting from a reduction to a one-dimensional problem (1-D) by integration on characteristic orbits are strongly affected by the trapped orbits, as here evaluated; a kernel calculation with a partial wave approximation is introduced. Dependencies from the local drift velocity
$z$ is the extraction axis), the undesired extraction of electrons from a negative ion source is reduced and it is due to collisions. The electron transport is studied with a kinetic model, including Vlasov–Poisson effects and atomic collisions. The integrodifferential equations (IDE) resulting from a reduction to a one-dimensional problem (1-D) by integration on characteristic orbits are strongly affected by the trapped orbits, as here evaluated; a kernel calculation with a partial wave approximation is introduced. Dependencies from the local drift velocity 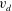 $v_{d}$ and effective Larmor radius
$v_{d}$ and effective Larmor radius 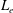 $L_{e}$ are found. Solutions are investigated in simple cases with a constant electron current (no additional electron production). Equilibrium solution and electron conductivity are analytically obtained. Presheath solutions are discussed; the approximated conversion to differential equations that are adequate for presheath only (with moderated electric field gradient
$L_{e}$ are found. Solutions are investigated in simple cases with a constant electron current (no additional electron production). Equilibrium solution and electron conductivity are analytically obtained. Presheath solutions are discussed; the approximated conversion to differential equations that are adequate for presheath only (with moderated electric field gradient 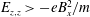 $E_{z,z}>-eB_{x}^{2}/m$) and their numeric solutions coupled to Poisson equation are reported, and compared to iterative IDE solutions. Examples with different values of
$E_{z,z}>-eB_{x}^{2}/m$) and their numeric solutions coupled to Poisson equation are reported, and compared to iterative IDE solutions. Examples with different values of 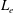 $L_{e}$ and mean free path (mfp) ratio are described.
$L_{e}$ and mean free path (mfp) ratio are described.
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press 2015
References
- 7
- Cited by


