Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Loizu, J.
and
Hudson, S. R.
2019.
Multi-region relaxed magnetohydrodynamic stability of a current sheet.
Physics of Plasmas,
Vol. 26,
Issue. 3,
Malhotra, Dhairya
Cerfon, Antoine
Imbert-Gérard, Lise-Marie
and
O'Neil, Michael
2019.
Taylor states in stellarators: A fast high-order boundary integral solver.
Journal of Computational Physics,
Vol. 397,
Issue. ,
p.
108791.
Henneberg, S.A.
Drevlak, M.
Nührenberg, C.
Beidler, C.D.
Turkin, Y.
Loizu, J.
and
Helander, P.
2019.
Properties of a new quasi-axisymmetric configuration.
Nuclear Fusion,
Vol. 59,
Issue. 2,
p.
026014.
Shanahan, B
Dudson, B
and
Hill, P
2019.
Fluid simulations of plasma filaments in stellarator geometries with BSTING.
Plasma Physics and Controlled Fusion,
Vol. 61,
Issue. 2,
p.
025007.
Suzuki, Yasuhiro
2020.
Effect of pressure profile on stochasticity of magnetic field in a conventional stellarator.
Plasma Physics and Controlled Fusion,
Vol. 62,
Issue. 10,
p.
104001.
Hudson, S R
Loizu, J
Zhu, C
Qu, Z S
Nührenberg, C
Lazerson, S
Smiet, C B
and
Hole, M J
2020.
Free-boundary MRxMHD equilibrium calculations using the stepped-pressure equilibrium code.
Plasma Physics and Controlled Fusion,
Vol. 62,
Issue. 8,
p.
084002.
Loizu, J.
Huang, Y.-M.
Hudson, S. R.
Baillod, A.
Kumar, A.
and
Qu, Z. S.
2020.
Direct prediction of nonlinear tearing mode saturation using a variational principle.
Physics of Plasmas,
Vol. 27,
Issue. 7,
Qu, Z S
Pfefferlé, D
Hudson, S R
Baillod, A
Kumar, A
Dewar, R L
and
Hole, M J
2020.
Coordinate parameterisation and spectral method optimisation for Beltrami field solver in stellarator geometry.
Plasma Physics and Controlled Fusion,
Vol. 62,
Issue. 12,
p.
124004.
Suzuki, Y.
Watanabe, K. Y.
and
Sakakibara, S.
2020.
Theoretical studies of equilibrium beta limit in LHD plasmas.
Physics of Plasmas,
Vol. 27,
Issue. 10,
Qu, Z S
Dewar, R L
Ebrahimi, F
Anderson, J K
Hudson, S R
and
Hole, M J
2020.
Stepped pressure equilibrium with relaxed flow and applications in reversed-field pinch plasmas.
Plasma Physics and Controlled Fusion,
Vol. 62,
Issue. 5,
p.
054002.
Rodríguez, E.
and
Bhattacharjee, A.
2021.
Islands and current singularities in quasisymmetric toroidal plasmas.
Physics of Plasmas,
Vol. 28,
Issue. 9,
Qu, Z S
Hudson, S R
Dewar, R L
Loizu, J
and
Hole, M J
2021.
On the non-existence of stepped-pressure equilibria far from symmetry.
Plasma Physics and Controlled Fusion,
Vol. 63,
Issue. 12,
p.
125007.
Aleynikova, K.
Hudson, S.R.
Helander, P.
Kumar, A.
Geiger, J.
Hirsch, M.
Loizu, J.
Nührenberg, C.
Rahbarnia, K.
Qu, Z.
Gao, Y.
Thomsen, H.
Turkin, Y.
Zanini, M.
and
W7-X Team, the
2021.
Model for current drive induced crash cycles in W7-X.
Nuclear Fusion,
Vol. 61,
Issue. 12,
p.
126040.
Baillod, A.
Loizu, J.
Qu, Z.S.
Kumar, A.
and
Graves, J.P.
2021.
Computation of multi-region, relaxed magnetohydrodynamic equilibria with prescribed toroidal current profile.
Journal of Plasma Physics,
Vol. 87,
Issue. 4,
Reiman, Allan H
2021.
Pressure-driven stochastization of flux surfaces in stellarator equilibria: a review of the experimental observations and their analysis.
Plasma Physics and Controlled Fusion,
Vol. 63,
Issue. 5,
p.
054002.
Landreman, Matt
2021.
Figures of merit for stellarators near the magnetic axis.
Journal of Plasma Physics,
Vol. 87,
Issue. 1,
Marcus, Frederick B.
2022.
Systems Approaches to Nuclear Fusion Reactors.
p.
321.
Hegna, C.C.
Anderson, D.T.
Bader, A.
Bechtel, T.A.
Bhattacharjee, A.
Cole, M.
Drevlak, M.
Duff, J.M.
Faber, B.J.
Hudson, S.R.
Kotschenreuther, M.
Kruger, T.G.
Landreman, M.
McKinney, I.J.
Paul, E.
Pueschel, M.J.
Schmitt, J.S.
Terry, P.W.
Ware, A.S.
Zarnstorff, M.
and
Zhu, C.
2022.
Improving the stellarator through advances in plasma theory.
Nuclear Fusion,
Vol. 62,
Issue. 4,
p.
042012.
Kumar, A
Nührenberg, C
Qu, Z
Hole, M J
Doak, J
Dewar, R L
Hudson, S R
Loizu, J
Aleynikova, K
Baillod, A
and
Hezaveh, H
2022.
Nature of ideal MHD instabilities as described by multi-region relaxed MHD.
Plasma Physics and Controlled Fusion,
Vol. 64,
Issue. 6,
p.
065001.
Baillod, A.
Loizu, J.
Graves, J. P.
and
Landreman, M.
2022.
Stellarator optimization for nested magnetic surfaces at finite β and toroidal current.
Physics of Plasmas,
Vol. 29,
Issue. 4,
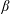 $\unicode[STIX]{x1D6FD}$-limit in a classical stellarator. The stepped-pressure equilibrium code (Hudson et al., Phys. Plasmas, vol. 19 (11), 2012) is used in order to assess whether or not magnetic islands and stochastic field-lines can emerge at high
$\unicode[STIX]{x1D6FD}$-limit in a classical stellarator. The stepped-pressure equilibrium code (Hudson et al., Phys. Plasmas, vol. 19 (11), 2012) is used in order to assess whether or not magnetic islands and stochastic field-lines can emerge at high 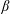 $\unicode[STIX]{x1D6FD}$. Two modes of operation are considered: a zero-net-current stellarator and a fixed-iota stellarator. Despite the fact that relaxation is allowed (Taylor, Rev. Mod. Phys., vol. 58 (3), 1986, pp. 741–763), the former is shown to maintain good flux surfaces up to the equilibrium
$\unicode[STIX]{x1D6FD}$. Two modes of operation are considered: a zero-net-current stellarator and a fixed-iota stellarator. Despite the fact that relaxation is allowed (Taylor, Rev. Mod. Phys., vol. 58 (3), 1986, pp. 741–763), the former is shown to maintain good flux surfaces up to the equilibrium 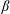 $\unicode[STIX]{x1D6FD}$-limit predicted by ideal-magnetohydrodynamics (MHD), above which a separatrix forms. The latter, which has no ideal equilibrium
$\unicode[STIX]{x1D6FD}$-limit predicted by ideal-magnetohydrodynamics (MHD), above which a separatrix forms. The latter, which has no ideal equilibrium 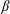 $\unicode[STIX]{x1D6FD}$-limit, is shown to develop regions of magnetic islands and chaos at sufficiently high
$\unicode[STIX]{x1D6FD}$-limit, is shown to develop regions of magnetic islands and chaos at sufficiently high 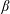 $\unicode[STIX]{x1D6FD}$, thereby providing a ‘non-ideal
$\unicode[STIX]{x1D6FD}$, thereby providing a ‘non-ideal 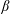 $\unicode[STIX]{x1D6FD}$-limit’. Perhaps surprisingly, however, the value of
$\unicode[STIX]{x1D6FD}$-limit’. Perhaps surprisingly, however, the value of 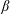 $\unicode[STIX]{x1D6FD}$ at which the Shafranov shift of the axis reaches a fraction of the minor radius follows in all cases the scaling laws predicted by ideal-MHD. We compare our results to the High-Beta-Stellarator theory of Freidberg (Ideal MHD, 2014, Cambridge University Press) and derive a new prediction for the non-ideal equilibrium
$\unicode[STIX]{x1D6FD}$ at which the Shafranov shift of the axis reaches a fraction of the minor radius follows in all cases the scaling laws predicted by ideal-MHD. We compare our results to the High-Beta-Stellarator theory of Freidberg (Ideal MHD, 2014, Cambridge University Press) and derive a new prediction for the non-ideal equilibrium 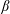 $\unicode[STIX]{x1D6FD}$-limit above which chaos emerges.
$\unicode[STIX]{x1D6FD}$-limit above which chaos emerges.

