Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-01-12T10:27:14.894Z Has data issue: false hasContentIssue false
  • English
  • Français

Collisional transport of impurities with flux-surface varying density in stellarators

Part of: Focus on Fusion

Published online by Cambridge University Press:  23 August 2018

S. Buller Open the ORCID record for S. Buller [Opens in a new window] ,
H. M. Smith ,
P. Helander ,
A. Mollén ,
S. L. Newton  and
I. Pusztai
S. Buller*
Affiliation:
Department of Physics, Chalmers University of Technology, SE-41296 Göteborg, Sweden
H. M. Smith
Affiliation:
Max-Planck-Institut für Plasmaphysik, 17491 Greifswald, Germany
P. Helander
Affiliation:
Max-Planck-Institut für Plasmaphysik, 17491 Greifswald, Germany
A. Mollén
Affiliation:
Max-Planck-Institut für Plasmaphysik, 17491 Greifswald, Germany
S. L. Newton
Affiliation:
CCFE, Culham Science Centre, Abingdon, Oxon OX14 3DB, UK
I. Pusztai
Affiliation:
Department of Physics, Chalmers University of Technology, SE-41296 Göteborg, Sweden
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

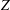High-$Z$ impurities in magnetic-confinement devices are prone to develop density variations on the flux surface, which can significantly affect their transport. In this paper, we generalize earlier analytic stellarator calculations of the neoclassical radial impurity flux in the mixed-collisionality regime (collisional impurities and low-collisionality bulk ions) to include the effect of such flux-surface variations. We find that only in the homogeneous density case is the transport of highly collisional impurities (in the Pfirsch–Schlüter regime) independent of the radial electric field. We study these effects for a Wendelstein 7-X (W7-X) vacuum field, with simple analytic models for the potential perturbation, under the assumption that the impurity density is given by a Boltzmann response to a perturbed potential. In the W7-X case studied, we find that larger amplitude potential perturbations cause the radial electric field to dominate the transport of the impurities. In addition, we find that classical impurity transport can be larger than the neoclassical transport in W7-X.

Keywords

fusion plasmaplasma confinement
Type
Research Article
Information
Journal of Plasma Physics , Volume 84 , Issue 4 , August 2018 , 905840409
Copyright
© Cambridge University Press 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Angioni, C. & Helander, P. 2014 Neoclassical transport of heavy impurities with poloidally asymmetric density distribution in tokamaks. Plasma Phys. Control. Fusion 56 (12), 124001.Google Scholar
Angioni, C., Mantica, P., Pütterich, T., Valisa, M., Baruzzo, M., Belli, E., Belo, P., Casson, F., Challis, C., Drewelow, P. et al. & JET EFDA Contributors 2014 Tungsten transport in JET H-mode plasmas in hybrid scenario, experimental observations and modelling. Nucl. Fusion 54 (8), 083028.Google Scholar
Braun, S. & Helander, P. 2010 Pfirsch–Schlüter impurity transport in stellarators. Phys. Plasmas 17 (7), 072514.Google Scholar
Calvo, I., Parra, F. I., Velasco, J. L., Alonso, J. A. & García-Regaña, J. M.2018 Stellarator impurity flux driven by electric fields tangent to magnetic surfaces. arXiv:1803.05691.Google Scholar
Fülöp, T. & Helander, P. 1999 Nonlinear neoclassical transport in a rotating impure plasma with large gradients. Phys. Plasmas 6 (8), 3066–3075.Google Scholar
García-Regaña, J., Beidler, C., Kleiber, R., Helander, P., Mollén, A., Alonso, J., Landreman, M., Maassberg, H., Smith, H., Turkin, Y. et al. 2017 Electrostatic potential variation on the flux surface and its impact on impurity transport. Nucl. Fusion 57 (5), 056004.Google Scholar
Hazeltine, R. D. 1973 Recursive derivation of drift-kinetic equation. Plasma Phys. 15 (1), 77.Google Scholar
Helander, P. 1998 Bifurcated neoclassical particle transport. Phys. Plasmas 5 (11), 3999–4004.Google Scholar
Helander, P. 2014 Theory of plasma confinement in non-axisymmetric magnetic fields. Rep. Progr. Phys. 77 (8), 087001.Google Scholar
Helander, P., Newton, S. L., Mollén, A. & Smith, H. M. 2017a Impurity transport in a mixed-collisionality stellarator plasma. Phys. Rev. Lett. 118, 155002.Google Scholar
Helander, P., Parra, F. I. & Newton, S. L. 2017b Stellarator bootstrap current and plasma flow velocity at low collisionality. J. Plasma Phys. 83 (2), 905830206.Google Scholar
Helander, P. & Sigmar, D. J. 2005 Collisional Transport in Magnetized Plasmas. Cambridge University Press.Google Scholar
Hirsch, M., Baldzuhn, J., Beidler, C., Brakel, R., Burhenn, R., Dinklage, A., Ehmler, H., Endler, M., Erckmann, V., Feng, Y. et al. 2008 Major results from the stellarator Wendelstein 7-AS. Plasma Phys. Control. Fusion 50 (5), 053001.Google Scholar
Kazakov, Y. O., Pusztai, I., Fülöp, T. & Johnson, T. 2012 Poloidal asymmetries due to ion cyclotron resonance heating. Plasma Phys. Control. Fusion 54 (10), 105010.Google Scholar
Mollén, A., Landreman, M., Smith, H. M., García-Regaña, J. M. & Nunami, M. 2018 Flux-surface variations of the electrostatic potential in stellarators: impact on the radial electric field and neoclassical impurity transport. Plasma Phys. Control. Fusion 60 (8), 084001.Google Scholar
Mollén, A., Pusztai, I., Fülöp, T., Kazakov, Y. O. & Moradi, S. 2012 Effect of poloidal asymmetries on impurity peaking in tokamaks. Phys. Plasmas 19 (5), 052307.Google Scholar
Mollén, A., Pusztai, I., Reinke, M. L., Kazakov, Y. O., Howard, N. T., Belli, E. A., Fülöp, T.& The Alcator C-Mod Team 2014 Impurity transport in Alcator C-Mod in the presence of poloidal density variation induced by ion cyclotron resonance heating. Plasma Phys. Control. Fusion 56 (12), 124005.Google Scholar
Nakajima, N., Okamoto, M., Todoroki, J., Nakamura, Y. & Wakatani, M. 1989 Optimization of the bootstrap current in a large helical system with $L=2$ . Nucl. Fusion 29 (4), 605–616.Google Scholar
Newton, S. L., Helander, P., Mollén, A. & Smith, H. M. 2017 Impurity transport and bulk ion flow in a mixed collisionality stellarator plasma. J. Plasma Phys. 83 (5), 905830505.Google Scholar
Rutherford, P. H. 1974 Impurity transport in the Pfirsch–Schlüter regime. Phys. Fluids 17 (9), 1782–1784.Google Scholar