1. INTRODUCTION
Traditional spacecraft navigation has been primarily done by means of range and range-rate measurements from the deep-space network (DSN). The major drawbacks to this approach are the high cost and the low update frequency. Both future robotic and human space exploration missions are expected to rely on autonomous operations more than ever before. Of particular interest here is the ability of a spacecraft to navigate autonomously independent of contact with Earth-based DSN or similar assets (Owen et al., Reference Owen2008; Riedel et al., Reference Riedel1997; Reference Riedel, Bhaskaran and Synnott2000; Reference Riedel2008; Wang and Huang, Reference Wang and Huang2009). For robotic missions, especially in the approach and landing phases, autonomous navigation is indispensable because Earth-based radio tracking navigation operations are severely limited due to communications constraints and low relative navigation accuracy. During the planetary approach, rendezvous and landing phases, some spacecraft have also relied on optical observations to improve the estimation of the spacecraft's situation with respect to the target planet or moon (Rush and Synnott, Reference Rush, Bhaskaran and Synnott2002; Bhaskaran et al., Reference Bhaskaran2011; Li et al., Reference Li, Cui and Cui2005). For manned missions, autonomous navigation would enable the crew to safely guide the spacecraft's return to Earth in the event of a radio tracking system failure. Autonomous navigation not only helps to reduce the communications demands on ground-based antennas but also helps provide the high-precision relative navigation. The latter is of great importance for landing and fly-by missions and is beyond the capability of the current ground-based tracking navigation (Owen et al., Reference Owen2008; Riedel et al., Reference Riedel2008; Owen, Reference Owen and William2011; Paluszek et al., Reference Paluszek, Mueller and Littman2010). Although, in the last two decades, several kinds of autonomous navigation methods and technologies have been proposed, autonomous optical navigation is considered the most feasible solution to the problem of spacecraft navigation without requiring ground-based tracking or status update (Owen, Reference Owen and William2011).
The feasibility of optical navigation (OPNAV) has been preliminarily confirmed by many deep-space missions. The NEAR Shoemaker mission depended heavily on an optical navigation system, which located many craters on the surface of the asteroid Eros as navigation landmarks and enabled rapid orbit determination around Eros (Owen, Reference Owen2001). For onboard navigation Hayabusa employed wide-angle cameras in conjunction with Light Detecting and Ranging (LIDAR) for measurement of altitude with respect to the asteroid Itokawa (Kominato, Reference Kominato2006). The OPNAV images captured by the NEAR and Hayabusa spacecraft were sent back to the Earth for image processing. These results were integrated with ground-based tracking data and then a status update was uploaded to the spacecraft. Deep Space 1, as part of the NASA New Millennium Program, used optical images of distant asteroids for orbit determination and was the first deep-space mission that used spacecraft autonomous navigation throughout the mission phases (Riedel et al., Reference Riedel1997; Reference Riedel, Bhaskaran and Synnott2000; Reference Riedel2008). The Deep Impact (DI) mission navigated the impactor spacecraft to successfully hit an illuminated area on the surface of comet Tempel 1, while also performing a fly-by of the main spacecraft to track the impact site (Riedel et al., Reference Riedel2008; Mastrodemos, Reference Mastrodemos2006; Owen, Reference Owen2006). From NEAR to Deep Impact, the most promising advance in optical navigation technology has been the migration from ground image processing to onboard processing, which consequently presents a huge challenge to the onboard computational capability.
The ultimate goal of image processing algorithms in optical navigation is to extract the various available navigation observables from raw images taken by a spacecraft, which usually include; the line-of-sight (LOS) vector, apparent diameter and centroid, angle between horizon and reference star, etc. (Owen, Reference Owen2008; Reference Owen and William2011). Among them, the LOS measurement is the most important. With the development of various deep-space flight missions, there have been many academic papers published on the subject of autonomous optical navigation. However, most of them are focused on the system dynamics, navigation measurement modeling and navigation filters; significantly few reported the onboard image processing algorithms and the procedure for the extraction of navigation observables (Giannatrapani et al., Reference Giannatrapani2011; Ma et al, Reference Ma, Liu and Meng2010; Li and Cui, Reference Li and Cui2008; Sui, Reference Sui, Yao and Zhao2008; Li et al., Reference Li, Cui and Cui2006; Sui et al., Reference Sui2007; Thompson et al., Reference Thompson.2012; Christian and Lightsey, Reference Christian and Lightsey2012). Traditional image processing algorithms face various difficulties and cannot be directly applied to an autonomous navigation system due to the low onboard computation capacity and the particularity of the deep-space environment (Owen, Reference Owen and William2011; Paluszek et al., Reference Paluszek, Mueller and Littman2010). The core requirement of image processing technologies for deep-space autonomous optical navigation lies in extracting navigation measurement information from various optical observations quickly and accurately. With the rapid development of optical sensors, image resolution is increasing exponentially, which usually results in a bigger computation burden and degrades real-time performance of autonomous optical navigation. Therefore, simple and effective image processing algorithms with a high degree of robustness are indispensable for the success of deep-space autonomous optical navigation.
The aim of this paper is to develop suitable image processing algorithms used for extracting navigation observables from raw grayscale images. The basic measurement obtained from this process is the line-of-sight (LOS) vector from the optical sensor to the centroid of the target celestial body, which is then input to a navigation filter in order to estimate the spacecraft status in combination with system dynamics equations. Image processing algorithms developed in this paper place emphasis on how to obtain the LOS measurement from a raw image regardless of other measurement types. This paper is structured as follows. Section 2 briefly presents the optical navigation measurement model and image processing algorithms involved in this paper. Section 3 describes the basic image processing techniques and Canny edge detection algorithm. Section 4 develops two new methodologies for fitting an ellipse to a set of limb data points. The centroid computation formula and the extraction procedure for navigation observables are given in Section 5. In section 6, simulation scenarios are described and results discussed in detail. Finally, Section 7 presents our conclusions and future work.
2. FUNDAMENTALS OF AUTONOMOUS OPTICAL NAVIGATION
2.1 Optical Navigation Measurement Model
The lowest order approximation to the optical sensor system is a pinhole camera model, which assumes every point on the target emits a single ray and that each ray maps to a point on the focal plane. A point P(X,Y,Z) is mapped to the imaging plane by the following relationship (Rafael and Richard, Reference Rafael and Richard2003):
 $$\eqalign{& u = \displaystyle{X \over Z}f \cr & v = \displaystyle{Y \over Z}f} $$
$$\eqalign{& u = \displaystyle{X \over Z}f \cr & v = \displaystyle{Y \over Z}f} $$where: u and v are coordinates in the focal plane, f is the focal length of navigation camera. X,Y,Z are defined in the camera-fixed frame, and Z is the distance from the pinhole to the point P(X,Y,Z) along the axis normal to the focal plane. This assumes that the Z-axis of the coordinate frame X,Y,Z is aligned with the boresight of the navigation camera.
The pinhole camera model allows for a simple relationship between a point on the detector plane and the corresponding line-of-sight unit vector. The relationship between the focal length, a measured point on the focal plane, and the line-of-sight unit vector to the image source is given by (Yi et al., Reference Yi, Jana and Stefano2004):
 $${\bf e}_i^C = \displaystyle{1 \over {\sqrt {u_i^2 + v_i^2 + f^2}}} \left[ \matrix{ - u_i \cr - v_i \cr f } \right]$$
$${\bf e}_i^C = \displaystyle{1 \over {\sqrt {u_i^2 + v_i^2 + f^2}}} \left[ \matrix{ - u_i \cr - v_i \cr f } \right]$$where the variable u i and v i are the coordinates of the point where the central ray of the i–th observed point source pierces the image plane.
The line-of-sight vector is then rotated from the camera frame to the inertial frame:
where T BI is the transformation matrix from body frame to inertial frame, and T CB is the transformation matrix from camera frame to body frame.
Imaging error sources, such as stellar aberration, parallax, stray light, misalignment and diffraction, are not included in the pinhole camera model. In order to get a real math model, both the external error sources and the internal camera error sources must be taken into account (Li and Lu, Reference Li and Lu2013).
2.2. Image Processing Procedure
In this paper, the image processing for autonomous optical navigation is a multi-step procedure. The first step is to simplify the raw image by using image pre-processing technologies to facilitate the subsequent steps. The second step is to identify the edge data points and remove the fake limb points. The third step is to find the limb profile in the image of a celestial object. For this third step, two different ellipse-fitting algorithms will be discussed: (1) the Least Squares based ellipse-fitting algorithm and (2) the Levenberg-Marquardt based ellipse-fitting algorithm. The last step is to compute the centroid according to the ellipse equation of the fitted limb profile. Thereafter, useful navigation measurements can be extracted. Figure 1 depicts a sketch of the image processing procedure; the details of these four steps are provided in the following subsections.

Figure 1. Sketch of the image processing procedure.
3. EDGES IDENTIFICATION ALGORITHM
3.1. Image Pre-Processing
The aim of image pre-processing technology is to make an image more suitable for subsequent processing. This is achieved by enhancing areas of interest and suppressing uninteresting regions without adding additional information. The method of pre-processing includes, among others, threshold segmentation, image smoothing, image sharpening and image correction technology (Rafael and Richard, Reference Rafael and Richard2003). In this paper they are directly applied to raw grayscale images taken by an optical navigation camera. Threshold segmentation operations can be used to simplify the raw image into a binary image and improve the running speed of subsequent image processing. Image smoothing operations can suppress imaging noise and other small fluctuations in the image which could cause blurring to sharp edges that bear important information about the image. On the other hand, image sharpening operations strengthen the edge features. Individually, each of these image processing techniques is rather simple. When properly combined, however, they can be a powerful tool and facilitate the following image processing. Figures 2 and 3, respectively, show the raw gray image of Mercury and the segmentation image with the threshold value τ = 0·1.

Figure 2. Raw gray image of Mercury.

Figure 3. Image after threshold segmentation (τ = 0·1).
3.2 Edge Detection
3.2.1. Canny Edge Detection
Edge points are defined as the points where the gradient magnitude assumes a local maximum in the gradient direction. An ideal edge detection algorithm is required to meet the following criteria: (1) noise should be effectively suppressed and (2) edge points should be accurately positioned. However, noise suppression and accurate positioning of edge points cannot be easily satisfied simultaneously. That is, the smoothing operation in edge detection can effectively remove the imaging noise; at the same time, it also weakens the main edge information of the original image. On the other hand, improving the sensitivity to the edge leads to the same adverse effects for noise suppression.
The first-order derivative of the Gaussian function is chosen here as a linear operator, which provides the best compromise between removing noise interference and accurate positioning of edge points (Canny, Reference Canny1986). In order to perform image smoothing using a Gaussian filter, we first introduce the Gaussian function as follows:
 $$G({i,j}) = e^{\left( { - \displaystyle{{i^2 + j^2} \over {2\sigma ^2}}} \right)} $$
$$G({i,j}) = e^{\left( { - \displaystyle{{i^2 + j^2} \over {2\sigma ^2}}} \right)} $$First, a convolution operation is implemented between the Gaussian function and the image intensity values:
where: * denotes the convolution operator and I(i,j) stands for the intensity values of the raw image.
Next, the first-order derivative finite difference of the image convolution in the horizontal direction (P [i,j]) and the vertical direction (Q [i,j]) can be obtained:
Then, the edge gradient magnitude M [i,j] and direction θ [i,j] can be determined as follows:
As the gradient magnitude of an edge point M [i,j] fulfills the condition of being a local maximum in the gradient direction, we use the Non-Maxima Suppression (NMS) technique to determine whether these local maximum data points belong to the edge points. We establish whether each pixel point [i,j] is a local maximum of the gradient magnitude among its adjacent pixels in the gradient direction and, if not, the gradient magnitude M [i,j] is set to zero. This screening process is sometimes referred to as edge thinning.
The final step of the Canny edge detection is detecting and connecting edge points using the double-threshold segmentation algorithm. Two threshold values are defined τ 1, τ 2 (τ 1>τ 2), and the magnitude of all the data points are set to zero when they are lower than the prescribed thresholds. Then, we can acquire two binary segmentation edge images T 1 and T 2, which correspond to the two different threshold values τ 1 and τ 2, respectively. If the threshold value is set too low, the segmentation result will be increasingly susceptible to imaging noise and will include some false edges. Conversely, segmentation with a high threshold may miss subtle edges and result in a fragmented edge profile. In order to overcome the problem of finding a suitable threshold, we first link the edge points obtained from higher threshold segmentation, and then the breakpoints are supplemented by edge points from lower threshold segmentation using the eight neighborhood search algorithm. Figure 4 depicts the result from Canny edge detection, which, obviously, includes the pseudo-edge. The removal of these pseudo-edges is described in the following section.

Figure 4. Canny edge detection result.
3.2.2. Pseudo-edge Removal
Taking into account the influence of the sun's azimuth and camera viewing angles, edge detection results, such as those from section 3.2.1., commonly contain some pseudo-edges due to the presence of backlight shaded areas. Pseudo-edges usually occur at the junction between the sunlight face and backlight face (Thompson et al., Reference Thompson.2012). In order to extract navigation information correctly, real edges must be distinguished from false edges.
False edges can be distinguished by the calculation of the angle between the lighting direction and the gradient direction of edges. The distribution of gradient direction is depicted in Figure 5. In fact, the angle between the gradient vectors of a planet's real edges and the sun lighting direction is less than 90°. Here, we assume that the sun lighting direction is provided by a sun sensor, though it can be obtained from a sophisticated image algorithm (Rafael and Richard, Reference Rafael and Richard2003). Given the planet's edge gradient vector g and the sun lighting direction n, the following relation should be satisfied:
The Inequality constraint (10) is the important criterion for identifying and eliminating the fake edges at the interface between the light and dark sides. Figure 6 shows that the real edges can be successfully identified after removing the pseudo-edges.

Figure 5. Edge gradient direction distribution.

Figure 6. Edge detection result without pseudo-edge.
4. LIMB PROFILE FITTING
The perspective projection of a sphere or ellipsoid will form an ellipse on the image plane. That is normally the case if the objective is to locate a planet or moon in an image. Once candidate edge points are found, an ellipse must be fitted to these data points. Most early solutions to the problem of ellipse fitting were based on clustering and voting techniques, such as the Hough transform (Zhang, Reference Zhang1997; Theodoridis and Koutroumbas, Reference Theodoridis and Koutroumbas2009). These techniques are naturally robust to noise and outliers; however, they require large amounts of memory and time-consuming computations, which leads to these algorithms being difficult to apply in an onboard computer.
4.1. Least Squares-Based Ellipse Fitting
All conic sections can be described by the following implicit quadratic equation (Brannan et al., Reference Brannan, Esplen and Gray1999):
where: [x i,yi] denotes the data point lying on the conic section. A detailed discussion of the properties of this implicit equation is given in (Brannan et al., Reference Brannan, Esplen and Gray1999) and it is well known that the conic will be an ellipse if the coefficients of equation (11) satisfy:
In general, the data points from the edge detection algorithm developed in Section 3 do not lie exactly on an ellipse and F(x i,yi)≠0 in the presence of imaging noise. Therefore, the following optimization problem based on the square of the model fitting residuals is proposed:
where: a=[A,B,C,D,E,F]T are the ellipse equation parameters to be estimated, f(a,xi)=Ax i2+Bx iyi+Cy i2+Dx i+Ey i+F stands for the estimated value from the ith observation point xi=(x i,yi), whose theoretical value should be zero, and n is the number of observation points.
Here, the ellipse fitting problem can be described as an optimization problem with the objective function to be minimized as follows:
 $$\min {{\{S({a})} }\} = \min \left\{ {\sum\limits_{i = 0}^m {\left[ {\,f\,({a},{x}_i )} \right]^2}} \right\}$$
$$\min {{\{S({a})} }\} = \min \left\{ {\sum\limits_{i = 0}^m {\left[ {\,f\,({a},{x}_i )} \right]^2}} \right\}$$According to extreme principle, the minimum value of S(a) can be obtained when the value of first order partial derivatives is zero:
Then the parameters of the ellipse can be determined when the objective function has a minimum:
The first order partial derivatives ![]() $\displaystyle{{\partial f} \over {\partial A}}$ can be rewritten as follows:
$\displaystyle{{\partial f} \over {\partial A}}$ can be rewritten as follows:
 $$\eqalign{ \displaystyle{{\partial f} \over {\partial A}}& = \displaystyle{{\partial \left(\sum\limits_{i = 1}^n {\left[ {\,f\,({a},{x}_i )} \right]^2} \right)} \over {\partial A}} = \sum\limits_{i = 1}^n {\displaystyle{{\partial \left[ {\,f\,({a},{x}_i )} \right]^2} \over {\partial A}}} \cr & = \sum\limits_{i = 1}^n {2(Ax_i^2 + Bx_i y_i + Cy_i^2 + Dx_i + Ey_i + F)} \cdot x_i^2 = 0} $$
$$\eqalign{ \displaystyle{{\partial f} \over {\partial A}}& = \displaystyle{{\partial \left(\sum\limits_{i = 1}^n {\left[ {\,f\,({a},{x}_i )} \right]^2} \right)} \over {\partial A}} = \sum\limits_{i = 1}^n {\displaystyle{{\partial \left[ {\,f\,({a},{x}_i )} \right]^2} \over {\partial A}}} \cr & = \sum\limits_{i = 1}^n {2(Ax_i^2 + Bx_i y_i + Cy_i^2 + Dx_i + Ey_i + F)} \cdot x_i^2 = 0} $$Similarly, we have
Linear equations (18)–(23) can be rewritten as follows:
 $$\left[ {\matrix{ {\sum\limits_{i = 1}^n {x_i^4}} & {\sum\limits_{i = 1}^n {x_i^3 y_i}} & {\sum\limits_{i = 1}^n {x_i^2 y_i^2}} & {\sum\limits_{i = 1}^n {x_i^3}} & {\sum\limits_{i = 1}^n {x_i^2 y_i}} & {\sum\limits_{i = 1}^n {x_i^2}} \cr {\sum\limits_{i = 1}^n {x_i^3 y_i}} & {\sum\limits_{i = 1}^n {x_i^2 y_i^2}} & {\sum\limits_{i = 1}^n {x_i y_i^3}} & {\sum\limits_{i = 1}^n {x_i^2 y_i}} & {\sum\limits_{i = 1}^n {x_i y_i^2}} & {\sum\limits_{i = 1}^n {x_i y_i}} \cr {\sum\limits_{i = 1}^n {x_i^2 y_i^2}} & {\sum\limits_{i = 1}^n {x_i y_i^3}} & {\sum\limits_{i = 1}^n {y_i^4}} & {\sum\limits_{i = 1}^n {x_i y_i^2}} & {\sum\limits_{i = 1}^n {y_i^3}} & {\sum\limits_{i = 1}^n {y_i^2}} \cr {\sum\limits_{i = 1}^n {x_i^3}} & {\sum\limits_{i = 1}^n {x_i^2 y_i}} & {\sum\limits_{i = 1}^n {x_i y_i^2}} & {\sum\limits_{i = 1}^n {x_i^2}} & {\sum\limits_{i = 1}^n {x_i y_i}} & {\sum\limits_{i = 1}^n {x_i}} \cr {\sum\limits_{i = 1}^n {x_i^2 y_i}} & {\sum\limits_{i = 1}^n {x_i y_i^2}} & {\sum\limits_{i = 1}^n {y_i^3}} & {\sum\limits_{i = 1}^n {x_i y_i}} & {\sum\limits_{i = 1}^n {y_i^2}} & {\sum\limits_{i = 1}^n {y_i}} \cr {\sum\limits_{i = 1}^n {x_i^2}} & {\sum\limits_{i = 1}^n {x_i y_i}} & {\sum\limits_{i = 1}^n {y_i^2}} & {\sum\limits_{i = 1}^n {x_i}} & {\sum\limits_{i = 1}^n {y_i}} & {\sum\limits_{i = 1}^n 1} \cr}} \right] \cdot \left[ {\matrix{ A \cr B \cr C \cr D \cr E \cr F \cr}} \right] = 0$$
$$\left[ {\matrix{ {\sum\limits_{i = 1}^n {x_i^4}} & {\sum\limits_{i = 1}^n {x_i^3 y_i}} & {\sum\limits_{i = 1}^n {x_i^2 y_i^2}} & {\sum\limits_{i = 1}^n {x_i^3}} & {\sum\limits_{i = 1}^n {x_i^2 y_i}} & {\sum\limits_{i = 1}^n {x_i^2}} \cr {\sum\limits_{i = 1}^n {x_i^3 y_i}} & {\sum\limits_{i = 1}^n {x_i^2 y_i^2}} & {\sum\limits_{i = 1}^n {x_i y_i^3}} & {\sum\limits_{i = 1}^n {x_i^2 y_i}} & {\sum\limits_{i = 1}^n {x_i y_i^2}} & {\sum\limits_{i = 1}^n {x_i y_i}} \cr {\sum\limits_{i = 1}^n {x_i^2 y_i^2}} & {\sum\limits_{i = 1}^n {x_i y_i^3}} & {\sum\limits_{i = 1}^n {y_i^4}} & {\sum\limits_{i = 1}^n {x_i y_i^2}} & {\sum\limits_{i = 1}^n {y_i^3}} & {\sum\limits_{i = 1}^n {y_i^2}} \cr {\sum\limits_{i = 1}^n {x_i^3}} & {\sum\limits_{i = 1}^n {x_i^2 y_i}} & {\sum\limits_{i = 1}^n {x_i y_i^2}} & {\sum\limits_{i = 1}^n {x_i^2}} & {\sum\limits_{i = 1}^n {x_i y_i}} & {\sum\limits_{i = 1}^n {x_i}} \cr {\sum\limits_{i = 1}^n {x_i^2 y_i}} & {\sum\limits_{i = 1}^n {x_i y_i^2}} & {\sum\limits_{i = 1}^n {y_i^3}} & {\sum\limits_{i = 1}^n {x_i y_i}} & {\sum\limits_{i = 1}^n {y_i^2}} & {\sum\limits_{i = 1}^n {y_i}} \cr {\sum\limits_{i = 1}^n {x_i^2}} & {\sum\limits_{i = 1}^n {x_i y_i}} & {\sum\limits_{i = 1}^n {y_i^2}} & {\sum\limits_{i = 1}^n {x_i}} & {\sum\limits_{i = 1}^n {y_i}} & {\sum\limits_{i = 1}^n 1} \cr}} \right] \cdot \left[ {\matrix{ A \cr B \cr C \cr D \cr E \cr F \cr}} \right] = 0$$ Defining the coefficient matrix 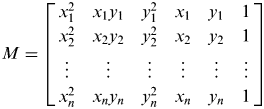 $M = \left[ \openup 2pt{\matrix{ {x_1^2} & {x_1 y_1} & {y_1^2} & {x_1} & {y_1} & 1 \cr {x_2^2} & {x_2 y_2} & {y_2^2} & {x_2} & {y_2} & 1 \cr \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \cr {x_n^2} & {x_n y_n} & {y_n^2} & {x_n} & {y_n} & 1 \cr}} \right]$, then these linear equations can be simplified into the following form:
$M = \left[ \openup 2pt{\matrix{ {x_1^2} & {x_1 y_1} & {y_1^2} & {x_1} & {y_1} & 1 \cr {x_2^2} & {x_2 y_2} & {y_2^2} & {x_2} & {y_2} & 1 \cr \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \cr {x_n^2} & {x_n y_n} & {y_n^2} & {x_n} & {y_n} & 1 \cr}} \right]$, then these linear equations can be simplified into the following form:
Generally speaking, for nonlinear equations, it is rather difficult, and sometimes even impossible, to directly find exact analytic solutions. However, an approximate solution can be obtained instead of the analytic solution by using numeric iteration methods such as Newton-Raphson iteration methods (Crassidis and Junkins, Reference Crassidis and Junkins2011). It should be noted that the equations simplified at (25) are linear equations, and, normally, the analytic solution can be easily obtained without complex iteration steps. Here, the Gaussian elimination method is utilized to solve the ellipse parameters A,B,C,D,E,F. It should be pointed out that the validity of these fitting parameters a should be checked according to the ellipse inequality constraint 4AC−B 2 > 0.
4.2. Levenberg-Marquardt-Based Ellipse Fitting
The Levenberg-Marquardt (LM) algorithm, also known as the damped least-squares method, provides a numerical solution to the problem of minimizing a nonlinear function. The Levenberg-Marquardt algorithm can effectively overcome: the difficulties of the nonlinear least squares approach, when an accurate initial estimate is not given; and the slow convergence problems of the steepest descent method, when the solution is close to minimizing the cost function (Crassidis and Junkins, Reference Crassidis and Junkins2011; Levenberg, Reference Levenberg1944). As with other numeric minimization algorithms, the Levenberg-Marquardt algorithm is an iterative procedure.
As before, the goal is to optimize the parameters a of the model curve f(a,x i) so that the sum of the squares of the deviations becomes minimal:
 $$\min \left\{ {S\left( {a} \right)} \right\} = \min \left\{ {\sum\limits_{i = 1}^n {\left[ {\,f\left( {{a},{x}_i} \right)} \right]^2}} \right\}$$
$$\min \left\{ {S\left( {a} \right)} \right\} = \min \left\{ {\sum\limits_{i = 1}^n {\left[ {\,f\left( {{a},{x}_i} \right)} \right]^2}} \right\}$$To start a minimization, an initial guess for the parameter vector a=[A,B,C,D,E,F]T is required. In each iteration step, the parameter vector a is then replaced by a new estimate a+δ. To determine the value of δ, the functions f(a+δ,x i) are approximated by their linearization:
where: ![]() $J_i = \displaystyle{{\partial f\,( {{a},{x}_i} )} \over {\partial {a}}}$ is the gradient of f with respect to a.
$J_i = \displaystyle{{\partial f\,( {{a},{x}_i} )} \over {\partial {a}}}$ is the gradient of f with respect to a.
At the minimum of the sum of squares S(a), the gradient of S with respect to δ should be zero. The above first-order approximation of f(a+δ,x i) gives:
or in vector notation:
Taking the derivative with respect to δ and setting it to zero ![]() $\displaystyle{{\partial S} \over {\partial {\delta}}} = 0$ gives:
$\displaystyle{{\partial S} \over {\partial {\delta}}} = 0$ gives:
where J is the Jacobian matrix whose i-th row equals J i, and where f(a) is the vector with i-th component f(a,x i).
In order to control the convergence rate and accuracy, a damping factor λ is introduced here. Equation (30) can be transformed as:
To avoid the defect of slow convergence in the direction of a small gradient, the identity matrix I is replaced with the diagonal matrix consisting of the diagonal elements diag(JTJ) (Crassidis and Junkins, Reference Crassidis and Junkins2011; Marquardt, Reference Marquardt1963).
All that is left to do is to solve the above linear equations, and then get the value of δ and the new ellipse parameter estimated value a+δ. With repeatedly iterated calculations, we can obtain the optimal estimate of afinal=(A,B,C,D,E,F)T. If these parameters meet the constraint condition 4AC−B 2>0, then we can conclude that afinal=(A,B,C,D,E,F)T is the optimal estimated ellipse parameters.
5. CENTROID EXTRACTION
The equation of the planet profile can thus be fitted by using the aforementioned methods of edge detection and ellipse fitting. Then the centre point of an ellipse can be assumed to be the centroid of a planet. Compared with a method directly extracting the centre-of-brightness (COB), the centroid approach achieves a better accuracy of navigation measurements with various influences, such as the shadows in an image of a planet which depend on the illumination and observation angles, and the interference of craters, texture, and atmosphere when photographed from a close range.
The centre of an ellipse can be obtained by the transformation from the implicit coefficients to standard ellipse parameters, which is a well-known result from classical geometry and is given by (Rafael and Richard, Reference Rafael and Richard2003; Yi et al., Reference Yi, Jana and Stefano2004):
 $$a = \sqrt {\displaystyle{{2\left[ {AE^2 + CD^2 - BDE + F\left( {B^2 - 4AC} \right)} \right]} \over {\left( {B^2 - 4AC} \right)\left[ {\sqrt {\left( {A - C} \right)^2 + B^2} - A - C} \right]}}} $$
$$a = \sqrt {\displaystyle{{2\left[ {AE^2 + CD^2 - BDE + F\left( {B^2 - 4AC} \right)} \right]} \over {\left( {B^2 - 4AC} \right)\left[ {\sqrt {\left( {A - C} \right)^2 + B^2} - A - C} \right]}}} $$ $$b = \sqrt {\displaystyle{{2\left[ {AE^2 + CD^2 - BDE + F\left( {B^2 - 4AC} \right)} \right]} \over {\left( {B^2 - 4AC} \right)\left[ { - \sqrt {\left( {A - C} \right)^2 + B^2} - A - C} \right]}}} $$
$$b = \sqrt {\displaystyle{{2\left[ {AE^2 + CD^2 - BDE + F\left( {B^2 - 4AC} \right)} \right]} \over {\left( {B^2 - 4AC} \right)\left[ { - \sqrt {\left( {A - C} \right)^2 + B^2} - A - C} \right]}}} $$ $$\phi = \left\{{\matrix{ {0{\kern 1pt}} & {B = 0\;and\;A \lt C} \cr {\displaystyle{\pi \over 2}} & {B = 0\;and\;A \gt C} \cr {\displaystyle{1 \over 2}\cot ^{ - 1} \left( {\displaystyle{{A - C} \over B}} \right)} & {B \ne 0\;and\;A \lt C} \cr {\displaystyle{\pi \over 2} + \displaystyle{1 \over 2}\cot ^{ - 1} \left( {\displaystyle{{A - C} \over B}} \right)} & {B \ne 0\;and\;A \gt C} \cr}} \right.$$
$$\phi = \left\{{\matrix{ {0{\kern 1pt}} & {B = 0\;and\;A \lt C} \cr {\displaystyle{\pi \over 2}} & {B = 0\;and\;A \gt C} \cr {\displaystyle{1 \over 2}\cot ^{ - 1} \left( {\displaystyle{{A - C} \over B}} \right)} & {B \ne 0\;and\;A \lt C} \cr {\displaystyle{\pi \over 2} + \displaystyle{1 \over 2}\cot ^{ - 1} \left( {\displaystyle{{A - C} \over B}} \right)} & {B \ne 0\;and\;A \gt C} \cr}} \right.$$where: (x 0,y 0) is the coordinate of the ellipse centre, a and b stand for the semi-major axis and the semi-minor axis, and ϕ is the inclined angle from the x-axis to the ellipse major axis.
The ellipse parameters obtained in Equations (33)–(37) include the coordinates of the ellipse centre, as well as the dimensions and orientation of the ellipse in the image plane. With these parameters we can easily compute the line-of-sight vector from the spacecraft to the centroid of a target celestial body according to Equations (2) and (3).
6. SIMULATION RESULTS AND ANALYSIS
In order to test the effectiveness and robustness of the image processing algorithm developed in this paper, real images obtained from deep-space flight missions and synthetic simulated images were utilized to test the performance of the image processing algorithm.
The real raw images used here come from the MESSENGER mission, which include a Mercury image (Product ID EN0108892844M) and a Venus image (Product ID N0089716371M) taken by the MESSENGER spacecraft's narrow angle camera on 15 January 2008 and 6 June 2007, respectively (Hash, Reference Hash2008). In order to find the potential edge profiles of the target celestial bodies in the image, the pre-processing and edge identification algorithms described in Section 3 were firstly applied to both the Mercury and Venus images. Then, the Least Squares-based ellipse fitting and Levenberg-Marquardt-based ellipse fitting algorithms were respectively implemented to fit the planet's limb profile. The simulation results are shown in Figures 7 and 8 respectively.

Figure 7. Image processing algorithm applied to real image containing Mercury. (Taken by MESSENGER on 15 January 2008).

Figure 8. Image processing algorithm applied to real image containing Venus. (Taken by MESSENGER on 6 June 2007).
Note that Figures 7 and 8 also contain two fitted ellipses, from the image processing algorithms developed in Section 4, superimposed in red or blue outlines on top of the raw Mercury and Venus images from the MESSENGER mission. The red outlines indicate the fitting ellipses obtained by the Least Squares-based ellipse fitting algorithm, and the blue outlines indicate the fitting ellipses obtained by the Levenberg-Marquardt-based ellipse fitting algorithm. It can be seen in these plots that both ellipse fitting algorithms accurately acquire the limb profiles of Mercury and Venus. It can also be observed that the pseudo-edge data points in the interior of the planet limb are all eliminated by the threshold segmentation operation, which is adopted before the Canny edge detection and aims at simplifying the raw image. At the same time, the fake edges produced at the interface between the light and dark areas can be effectively removed by considering the angle between the planet's edge gradient vectors and the lighting direction, which greatly contributes to the success of the planet profile fitting algorithm.
Synthetic images were also used in our simulation analysis to test the robustness of image processing algorithms developed in this paper. When the solar azimuth angle is provided by an onboard attitude sensor, synthetic images of a planet or moon can be generated using the suitable optical imaging theories and models. The principle and process of how to produce real simulated images including various imaging errors will be described in detail in a companion paper (Li and Lu, Reference Li and Lu2013) and, thus, are not detailed here. Simulated planet images with various surface textures and solar azimuth angles can be found in Figures 9 through 11. Figure 9 shows the simulated flat surface image of a distant planet with a 60 degrees solar azimuth angle. Figure 10 depicts the simulated image of a planet covered with crater texture at 45 degrees solar azimuth angle. A synthetic image of a planet covered with atmosphere is represented in Figure 11 at an illumination phase angle of 30 degrees.

Figure 9. Simulated image of a planet with flat surface.

Figure 10. Simulated image of a planet with crater texture.

Figure 11. Simulated image of a planet with atmosphere.
Then, the complete image processing algorithms developed in this paper, including both the Least Squares and the Levenberg-Marquardt ellipse fitting algorithms, are applied to the three simulated images of a planet with different surface textures and sun azimuth angles, and the results are plotted in Figure 12 for comparison. It should be noted that the image processing algorithms can accurately obtain the limb profiles of the planets with different textures and lighting conditions. The effectiveness and robustness of the image processing algorithm developed in this paper can, therefore, be preliminarily confirmed.

Figure 12. Image processing algorithm applied to simulated images of a distant planet.
To further verify the performance of the ellipse fitting algorithms described in Section 4, simulation and analysis using different fitting algorithms and different simulated images are performed for comparison. It is emphasized that all the simulations adopted the same image processing algorithm developed in this paper except for the ellipse fitting portion. The method of improved ellipse fitting with direct Least-Squares estimation presented by Christian and Lightsey (Reference Christian and Lightsey2012) is used as a reference compared with the two ellipse fitting algorithms described in Section 4. All three simulated images (covered with a flat surface, crater texture and atmosphere) are included in our simulation and test. As the ellipse parameters of the limb profile in the simulated images can be accurately known in advance, the fitting errors can be easily obtained after the profile ellipses are fitted. The fitting errors of the three ellipse fitting algorithms are shown in Tables 1 through 3, respectively. It can be seen from these tables that the maximum fitting error with the method of improved ellipse fitting with direct least-squares estimation is larger than three pixels, while the maximum errors with both the Least Squares-based ellipse fitting and the Levenberg-Marquardt-based ellipse fitting algorithms, are less than three pixels. It should also be noted that the inclined angle error in Table 1 is equal to zero, which indicates that the Least Squares-based ellipse fitting algorithm is insensitive to errors in the ellipse orientation angle.
Table 1. Fitting error of Least Squares-based ellipse fitting algorithm.

Table 2. Fitting error of improved ellipse fitting with direct least-squares estimation.

Tables 1 to Table 3 set out the fitting errors of three ellipse fitting algorithms, but it is still difficult to make useful comparisons of their performance from just these tables. When the relevant parameters of the camera system are given, we can easily convert the ellipse fitting error into an error on the observed line-of-sight vector, which is directly related to the navigation accuracy and very suitable to be used to determine the performance of the three ellipse fitting algorithms. Assume the focal length of the camera f = 200 mm, the angle of view field θ = 3·5°, scale factor K x = K y = 83·8 pixel/mm, then the observation errors of the line-of-sight vector from the camera to centre of the planet can be found in Table 4.
Table 3. Fitting error of Levenberg-Marquardt based ellipse fitting algorithm.

Table 4. Error of the line-of-sight vector.

It can be seen from Tables 1 to 4 that, when compared with the reference algorithm presented in Christian and Lightsey (Reference Christian and Lightsey2012), that the two methods proposed in this paper lead to a better fitting accuracy. The fitting errors of ellipse centre, semi-major and semi-minor axes are less than three pixels, and the error of the line-of-sight vector to the object centre is less than 1·67 × 10−4 rad, which can meet the requirements of deep-space autonomous navigation. Given the illustrated performance of these two algorithms in the different simulation scenarios, we can conclude that the Least Squares-based ellipse fitting algorithm works well in the case of good illumination conditions and low background noise, and the Levenberg-Marquardt-based ellipse fitting algorithm will deliver a better accuracy of profile fitting when visibility is poor with much noise. An interesting result here is that the improved ellipse fitting with the direct Least-Squares estimation algorithm works better than our proposed algorithms only with the simulated images covered by a flat texture. When simulated images covered by a crater texture or atmosphere are taken into account, both the Least Squares-based ellipse fitting and the Levenberg-Marquardt-based ellipse fitting algorithms outperform the Improved Ellipse Fitting with Direct Least-Squares Estimation algorithm, and the Levenberg-Marquardt-based ellipse fitting algorithm is superior to the other two. It is noteworthy that a simulated image covered by a flat surface texture presents almost no imaging noise, while simulated images with a crater texture or atmosphere usually include a large number of imaging noises. So, a conclusion can be drawn that the Least Squares-based ellipse fitting and the Improved Ellipse Fitting with direct Least-Squares estimation algorithms work well in a low background noise environment; in contrast, the Levenberg-Marquardt-based ellipse fitting algorithm performs better, and is more reliable, in a high noise environment. The main reason why both the algorithms developed in this paper outperform the reference algorithm in Christian and Lightsey (Reference Christian and Lightsey2012) in high noise cases is the fact that the latter depends heavily on the location distribution of the edge data points and thus is also more sensitive to the presence of outliers. It can be seen from Table 4 that improved ellipse fitting with direct least-squares estimation performs best among all the tests in the case of simulated image covered by a flat surface. In this situation, there are few outliers and the quality of edge characteristics is fairly good. In fact, various factors and limitations in real flight missions, such as imaging noise and resolution, result in the real flight image being covered by complicated textures and noise, which inevitably gives rise to a lot of outliers.
7. CONCLUSION
The capability of autonomous optical navigation (OPNAV) is crucial for future robotics and manned deep-space exploration missions. New image processing algorithms, in particular Least Squares-based ellipse fitting and Levenberg-Marquardt-based ellipse fitting algorithms, are developed in this paper to meet the requirements of deep-space autonomous OPNAV. Both simulated images and real flight images from the MESSENGER mission are utilized to test the performance of the image processing algorithm developed in this paper. Simulation results show that the two methods proposed can accurately extract the navigation observables from the raw images. The maximum ellipse fitting errors are less than three pixels, and the error of the line-of-sight vector to the object centre is less than 1·67 × 10−4 rad, which can meet the requirements of deep-space autonomous navigation.
Future work will focus on an end-to-end assessment of the performance of a complete autonomous OPNAV algorithm, which will systematically incorporate the image processing algorithm developed in this paper with a representative dynamics model and navigation filter algorithm.
ACKNOWLEDGEMENTS
The work described in this paper was supported by: the National Natural Science Foundation of China (Grant No. 61273051 and 60804057), National High Technology Research and Development Program of China (Grant No. 2011AA7034057E), Innovation Funded Project of Shanghai Aerospace Science and Technology (Grant No. SAST201213) and Qing Lan Project of Jiangsu Province. The author fully appreciates their financial support. The authors are grateful to Dr Daniel García Yárnoz and Joan-Pau Sanchez Cuartielles from the University of Strathclyde, for their assistance in grammatical improvement.


















