Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-24T02:37:42.583Z Has data issue: false hasContentIssue false
  • English
  • Français

The Arithmetic of Navigation Position Errors

Published online by Cambridge University Press:  23 November 2009

J. B. Parker
Get access Rights & Permissions [Opens in a new window]

Extract

In a notable series of articles, Hsu advances theoretical models which are used to graduate 7582 observations of aircraft lateral deviations. The goodness of fit of these models, as judged by the χ2 test, is satisfactory. Hsu's main theoretical model is the Double Double Exponential distribution (DDE), a three parameter model whose probability density function is given by

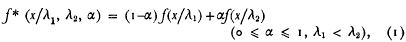
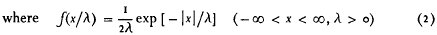
Other model types are also considered, such as the family of exponential power distributions whose probability density is cited by Hsu insection 9. This leads to a four-parameter model, and the fit is (not surprisingly) better even than that of the DDE.

Type
Research Article
Information
The Journal of Navigation , Volume 35 , Issue 1 , January 1982 , pp. 28 - 38
Copyright
Copyright © The Royal Institute of Navigation 1982

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

1Hsu, D. A. (1979). Long tailed distributions for position errors in navigation. Journal of the Royal Statistical Society, series C (Applied Statistics), 28, 62–72Google Scholar
2Hsu, D. A. (1980). Further analyses of position errors in navigation. This Journal, 33, 453.Google Scholar
3Hsu, D. A. (1981). The evaluation of aircraft collision probabilities at intersecting air routes. This Journal, 34, 78.Google Scholar
4Polhemus, N. W. and Livingston, D. (1981). Characterizing cross-track error distributions for continental jet routes. This Journal, 34, 134.Google Scholar
5Anderson, E. W. and Ellis, D. M. (1971). Error distributions in navigation. This Journal, 24, 429.Google Scholar
6Hsu, D. A. (1979). An analysis of error distributions in navigation. This Journal, 32, 426.Google Scholar
7Kendall, M. G. and Stuart, A. (1976). The Advanced Theory of Statistics, vol. 3, chapter 46, 380.Google Scholar
8Box, G. E. P. (1980). Sampling and Bayes' inference in scientific modelling and robustness. Journal of the Royal Statistical Society, series A (General), 143, 383 (specifically see p. 397).Google Scholar